Counting to n

Let’s now generalize the previous exercise from using a fixed number of threads (2) to using an an arbitrary number of threads. Specifically, we’ll verify the equivalent of the following Rust program:

• The main thread instantiates a counter to 0.
• The main thread forks num_threads child threads.
  • Each child thread (atomically) increments the counter.
• The main thread joins all the threads (i.e., waits for them to complete).
• The main thread reads the counter.

Our objective: Prove the counter read in the final step has value num_threads.

// Ordinary Rust code, not Verus

use std::sync::atomic::{AtomicU32, Ordering};
use std::sync::Arc;
use std::thread::spawn;

fn do_count(num_threads: u32) {
    // Initialize an atomic variable

    let atomic = AtomicU32::new(0);

    // Put it in an Arc so it can be shared by multiple threads.

    let shared_atomic = Arc::new(atomic);

    // Spawn `num_threads` threads to increment the atomic once.

    let mut handles = Vec::new();

    for _i in 0..num_threads {
        let handle = {
            let shared_atomic = shared_atomic.clone();
            spawn(move || {
                shared_atomic.fetch_add(1, Ordering::SeqCst);
            })
        };
        handles.push(handle);
    }

    // Wait on all threads. Exit if an unexpected condition occurs.

    for handle in handles.into_iter() {
        match handle.join() {
            Result::Ok(()) => {}
            _ => {
                return;
            }
        };
    }

    // Load the value, and assert that it should now be `num_threads`.

    let val = shared_atomic.load(Ordering::SeqCst);
    assert!(val == num_threads);
}

fn main() {
    do_count(20);
}

Verified implementation

We’ll build off the previous exercise here, so make sure you’re familiar with that one first.

Our first step towards verifying the generalized program is to update the tokenized_state_machine from the earlier example. Recall that in that example, we had two boolean fields, inc_a and inc_b, to represent the two tickets. This time, we will merely maintain counts of the number of tickets: we’ll have one field for the number of unstamped tickets and one for the number of stamped tickets.

Let’s start with the updated state machine, but ignore the tokenization aspect for now. Here’s the updated state machine as an atomic state machine:

state_machine! {
    X {
        fields {
            pub num_threads: nat,
            pub counter: int,
            pub unstamped_tickets: nat,
            pub stamped_tickets: nat,
        }

        #[invariant]
        pub fn main_inv(&self) -> bool {
            self.counter == self.stamped_tickets
            && self.stamped_tickets + self.unstamped_tickets == self.num_threads
        }

        init!{
            initialize(num_threads: nat) {
                init num_threads = num_threads;
                init counter = 0;
                init unstamped_tickets = num_threads;
                init stamped_tickets = 0;
            }
        }

        transition!{
            tr_inc() {
                // Replace a single unstamped ticket with a stamped ticket
                require(pre.unstamped_tickets >= 1);
                update unstamped_tickets = (pre.unstamped_tickets - 1) as nat;
                update stamped_tickets = pre.stamped_tickets + 1;

                assert(pre.counter < pre.num_threads);
                update counter = pre.counter + 1;
            }
        }

        property!{
            finalize() {
                require(pre.stamped_tickets >= pre.num_threads);
                assert(pre.counter == pre.num_threads);
            }
        }

        // ... invariant proofs here
    }
}

Note that we added a new field, num_threads, and we replaced inc_a and inc_b with unstamped_tickets and stampted_tickets.

Now, let’s talk about the tokenization. In the previous example, all of our fields used the variable strategy, but we never got a chance to talk about what that meant. Let’s now see some of the other strategies.

For our new program, we will need to make two changes.

The constant strategy

First, the num_threads can be marked as a constant, since this value is really just a parameter to the protocol, and will be fixed for any given instance of it. By marking it constant, we won’t get a token for it, but instead the value will be available from the shared Instance object.

The count strategy

This change is far more subtle. The key problem we need to solve is that the “tickets” need to be spread across multiple threads. However, if unstamped_tickets and stamped_tickets were marked as variable then we would only get one token for each field.

Recall our physical analogy with the tickets and the chalkboard (used for the counter field), and compare: there’s actually something fundamentally different about the tickets and the chalkboard, which is that the tickets are actually a count of something. Think of it this way:

• If Alice has 3 tickets, and Bob has 2 tickets, then together they have 5 tickets.
• If Alice has a chalkboard with the number 3 written on it, and Bob has a chalkboard with the number 2 on it, then together do they have a chalkboard with the number 5 written on it?
  • No! They just have two chalkboards with 2 and 3 written on them. In fact, in our scenario, we aren’t even supposed to have more than 1 chalkboard anyway. Alice and Bob are in an invalid state here.

We need a way to mark this distinction, that is, we need a way to be able to say, “this field is a value on a chalkboard” versus “the field indicates the number of some thing”. The variable strategy we have been using until now is the former; the newly introduce count strategy is the latter. Thus, we need to use the count strategy for the ticket fields.

We need to mark the ticket fields as being a “count” of something, and this is exactly what the count strategy is for. Rather than having exactly one token for the field value, the count strategy will make it so that the field value is the sum total of all the tokens in the system associated with that field. (However, this new flexibility will come with some restrictions, as we will see.)

Here, we can visualize how the ghost tokens are spread throughout the running system, and how they relate to the global state:

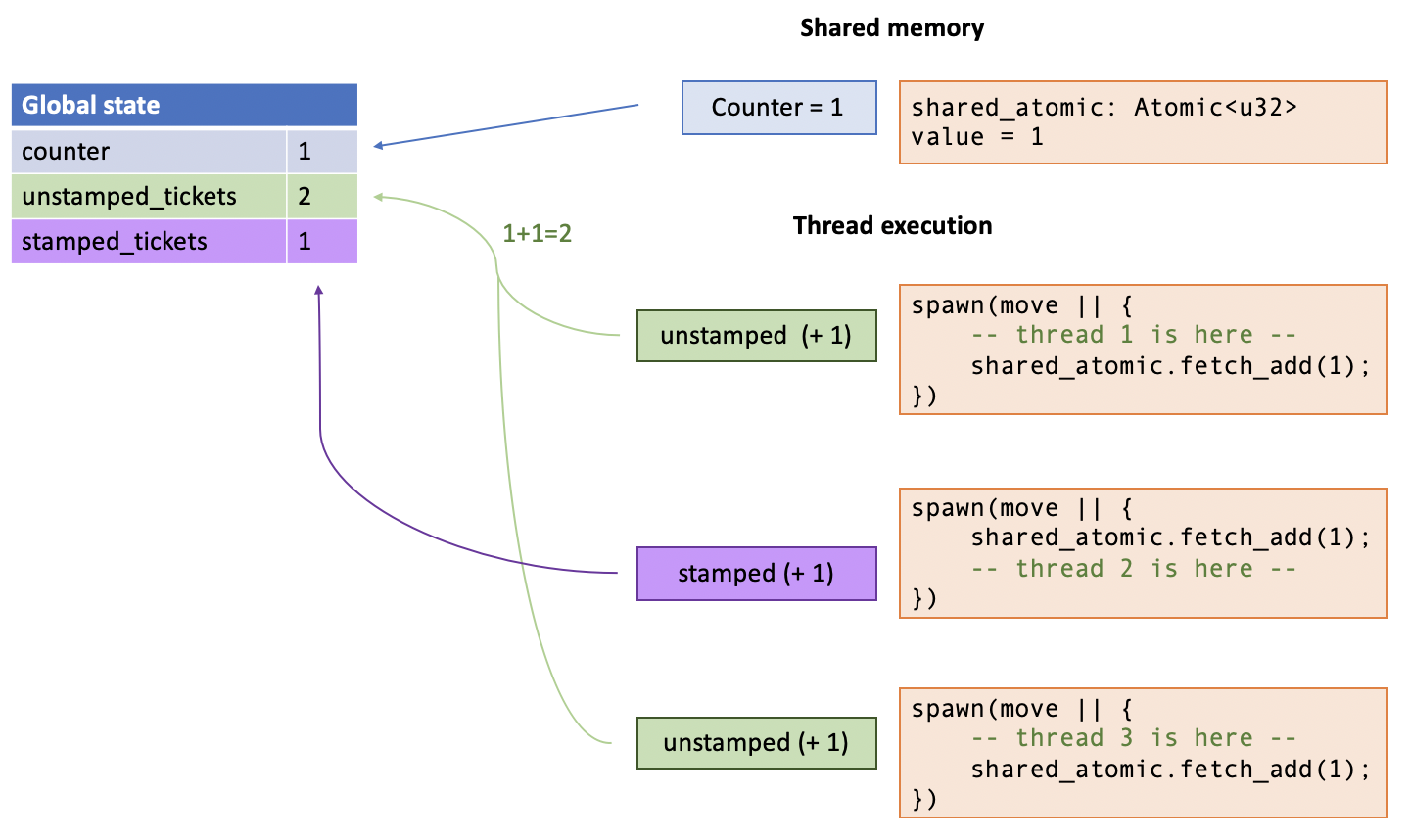
In this scenario, we have three threads, all of which are currenlty executing, where thread 2 has incremented the counter, but threads 1 and 3 have not. Thus, threads 1 and 3 each have an “unstamped ticket” token, while thread 2 has a “stamped ticket” token. The abstract global state, then, has unstamped_tickets == 2 and stamped_tickets == 1.

Building the new tokenized_state_machine

First, we mark the fields with the appropriate strategies, as we discussed:

tokenized_state_machine!{
    X {
        fields {
            #[sharding(constant)]
            pub num_threads: nat,

            #[sharding(variable)]
            pub counter: int,

            #[sharding(count)]
            pub unstamped_tickets: nat,

            #[sharding(count)]
            pub stamped_tickets: nat,
        }

Just by marking the strategies, we can already see how it impacts the generated token code. Let’s look at unstamped_tickets (the stamped_tickets is, of course, similar):

// Code auto-generated by tokenized_state_machine! macro

#[proof]
#[verifier(unforgeable)]
pub struct unstamped_tickets {
    #[spec] pub instance: Instance,
    #[spec] pub value: nat,
}

impl unstamped_tickets {
    #[proof]
    #[verifier(returns(proof))]
    pub fn join(#[proof] self, #[proof] other: Self) -> Self {
        requires(equal(self.instance, other.instance));
        ensures(|s: Self| {
            equal(s.instance, self.instance)
                && equal(s.value, self.value + other.value)
        });

        // ...
    }

    #[proof]
    #[verifier(returns(proof))]
    pub fn split(#[proof] self, #[spec] i: nat) -> (Self, Self) {
        requires(i <= self.value);
        ensures(|s: (Self, Self)| {
             equal(s.0.instance, self.instance)
                && equal(s.1.instance, self.instance)
                && equal(s.0.value, i)
                && equal(s.1.value, self.value - i)
        });

        // ...
    }
}

The token type, unstamped_tickets comes free with 2 associated methods, join and split. First, join lets us take two tokens with an associate count and merge them together to get a single token with the combined count value; meanwhile, split goes the other way. So for example, when we start out with a single token of count num_threads, we can split into num_threads tokens, each with count 1.

Now, let’s move on to the rest of the system. Our invariant and the initialization routine will be identical to before. (In general, init statements are used for all sharding strategies. The sharding strategies might affect the token method that gets generated, but the init! definition itself will remain the same.)

        #[invariant]
        pub fn main_inv(&self) -> bool {
            self.counter == self.stamped_tickets
            && self.stamped_tickets + self.unstamped_tickets == self.num_threads
        }

        init!{
            initialize(num_threads: nat) {
                init num_threads = num_threads;
                init counter = 0;
                init unstamped_tickets = num_threads;
                init stamped_tickets = 0;
            }
        }

The tr_inc definition is where it gets interesting. Let’s take a closer look at the definition we gave earlier:

        transition!{
            tr_inc() {
                // Replace a single unstamped ticket with a stamped ticket
                require(pre.unstamped_tickets >= 1); 
                update unstamped_tickets = pre.unstamped_tickets - 1;
                update stamped_tickets = pre.stamped_tickets + 1;

                assert(pre.counter < pre.num_threads);
                update counter = pre.counter + 1;
            }   
        }  

There’s a problem here, which is that the operation directly accesses pre.unstamped_tickets and writes to the same field with an update statement, and likewise for the stamped_tickets field. Because these fields are marked with the count strategy, Verus will reject this definition.

So why does Verus have to reject it? Keep in mind that whatever definition we give here, Verus has to be able to create a transition definition that works in the tokenized view of the world. In any tokenized transition, the tokens that serve as input must by themselves be able to justify the validity of the transition being performed.

Unfortunately, this justification is impossible when we are using the count strategy. When the field is tokenized according to the count strategy, there is no way for a client to produce a set of tokens that definitively determines the value of the unstamped_tickets field in the global state machine. For instance, suppose the client provides three such tokens; this does not necessarily means that pre.unstamped_tickets is equal to 3! Rather, there might be other tokens elsewhere in the system held on by other threads, so all we can justify from the existence of those tokens is that pre.unstamped_tickets is greater than or equal to 3.

Thus, Verus demands that we do not read or write to the field arbitrarily. Effectively, we can only perform operations that look like one of the following for a count-strategy field:

• Require the field’s value to be greater than some natural number
• Subtract a natural number
• Add a natural number

Luckily, we can see that the transition from earlier only does these allowed things. To get Verus to accept it, we only need to write the transition using a special syntax so that it can identify the patterns involved.

        transition!{
            tr_inc() {
                // Equivalent to:
                //    require(pre.unstamped_tickets >= 1);
                //    update unstampted_tickets = pre.unstamped_tickets - 1
                // (In any `remove` statement, the `>=` condition is always implicit.)
                remove unstamped_tickets -= (1);

                // Equivalent to:
                //    update stamped_tickets = pre.stamped_tickets + 1
                add stamped_tickets += (1);

                // These still use ordinary 'update' syntax, because `pre.counter`
                // uses the `variable` sharding strategy.
                assert(pre.counter < pre.num_threads);
                update counter = pre.counter + 1;
            }
        }

Generally, a remove corresponds to destroying a token, while add corresponds to creating a token. Thus the generated exchange function takes an unstamped_tickets token as input and gives a stamped_tickets token as output. Ultimately, thus, it exchanges an unstamped ticket for a stamped ticket.

// Code auto-generated by tokenized_state_machine! macro

#[proof]
#[verifier(returns(proof))]
pub fn tr_inc(
    #[proof] &self,
    #[proof] token_counter: &mut counter,
    #[proof] token_0_unstamped_tickets: unstamped_tickets, // input (destroyed)
) -> stamped_tickets                                       // output (created)
{
    requires([
        equal(old(token_counter).instance, (*self)),
        equal(token_0_unstamped_tickets.instance, (*self)),
        equal(token_0_unstamped_tickets.value, 1),                      // remove unstamped_tickets -= (1);
    ]);
    ensures(|token_1_stamped_tickets: stamped_tickets| {
        [
            equal(token_counter.instance, (*self)),
            equal(token_1_stamped_tickets.instance, (*self)),
            equal(token_1_stamped_tickets.value, 1),                    // add stamped_tickets += (1);
            (old(token_counter).value < (*self).num_threads()),         // assert(pre.counter < pre.num_threads);
            equal(token_counter.value, old(token_counter).value + 1),   // update counter = pre.counter + 1;
        ]
    });

    // ...
}

The finalize transition needs to be updated in a similar way:

        property!{
            finalize() {
                // Equivalent to:
                //    require(pre.unstamped_tickets >= pre.num_threads);
                have stamped_tickets >= (pre.num_threads);

                assert(pre.counter == pre.num_threads);
            }
        }

The have statement is similar to remove, except that it doesn’t do the remove. It just requires the client to provide tokens counting in total at least pre.num_threads here, but it doesn’t consume them.

Again, notice that the condition we have to write is equivalent to a >= condition. We can’t just require that stamped_tickets == pre.num_threads.

(Incidentally, it does happen to be the case that pre.stamped_tickets >= pre.num_threads implies that pre.stamped_tickets == pre.num_threads. This implication follows from the the invariant, but it isn’t something we know a priori. Therefore, it is still the case that we have to write the transition with the weaker requirement that pre.stamped_tickets >= pre.num_threads. The safety proof will then deduce that pre.stamped_tickets == pre.num_threads from the invariant, and then deduce that pre.counter == pre.num_threads, which is what we really want in the end.)

// Code auto-generated by tokenized_state_machine! macro

#[proof]
pub fn finalize(
    #[proof] &self,
    #[proof] token_counter: &counter,
    #[proof] token_0_stamped_tickets: &stamped_tickets,
) {
    requires([
        equal(token_counter.instance, (*self)),
        equal(token_0_stamped_tickets.instance, (*self)),
        equal(token_0_stamped_tickets.value, (*self).num_threads()),     // have stamped_tickets >= (pre.num_threads);
    ]);
    ensures([(token_counter.value == (*self).num_threads())]);           // assert(pre.counter == pre.num_threads);

    // ...
}

Verified Implementation

The implementation of a thread’s action hasn’t change much from before. The only difference is that we are now exchanging an unstamped_ticket for a stamped_ticket, rather than updating a boolean field.

Perhaps more interesting now is the main function which does the spawning and joining. It has to spawn threads in a loop. Note that we start with a stamped_tokens count of num_threads. Each iteration of the loop, we “peel off” a single ticket (1 unit’s worth) and pass it into the newly spawned thread.

    // Spawn threads
    let mut join_handles: Vec<JoinHandle<Tracked<X::stamped_tickets>>> = Vec::new();
    let mut i = 0;
    while i < num_threads
        invariant
            0 <= i,
            i <= num_threads,
            unstamped_tokens@.count + i as int == num_threads as int,
            unstamped_tokens@.instance === instance,
            join_handles@.len() == i as int,
            forall|j: int, ret|
                0 <= j && j < i ==> join_handles@.index(j).predicate(ret) ==> ret@@.instance
                    === instance && ret@@.count == 1,
            (*global_arc).wf(),
            (*global_arc).instance@ === instance,
    {
        let tracked unstamped_token;
        proof {
            let tracked (Tracked(unstamped_token0), Tracked(rest)) = unstamped_tokens.split(
                1 as nat,
            );
            unstamped_tokens = rest;
            unstamped_token = unstamped_token0;
        }
        let global_arc = global_arc.clone();
        let join_handle = spawn(
            (move || -> (new_token: Tracked<X::stamped_tickets>)
                ensures
                    new_token@@.instance == instance,
                    new_token@@.count == 1nat,
                {
                    let tracked unstamped_token = unstamped_token;
                    let globals = &*global_arc;
                    let tracked stamped_token;
                    let _ =
                        atomic_with_ghost!(
                            &global_arc.atomic => fetch_add(1);
                            update prev -> next;
                            returning ret;
                            ghost c => {
                                stamped_token =
                                    global_arc.instance.borrow().tr_inc(&mut c, unstamped_token);
                            }
                        );
                    Tracked(stamped_token)
                }),
        );
        join_handles.push(join_handle);
        i = i + 1;
    }

Then, when we join the threads, we do the opposite: we collect the “stamped ticket” tokens until we have collected all num_threads of them.

    // Join threads

    let mut i = 0;
    while i < num_threads
        invariant
            0 <= i,
            i <= num_threads,
            stamped_tokens@.count == i as int,
            stamped_tokens@.instance === instance,
            join_handles@.len() as int + i as int == num_threads,
            forall|j: int, ret|
                0 <= j && j < join_handles@.len() ==> #[trigger] join_handles@.index(j).predicate(
                    ret,
                ) ==> ret@@.instance === instance && ret@@.count == 1,
            (*global_arc).wf(),
            (*global_arc).instance@ === instance,
    {
        let join_handle = join_handles.pop().unwrap();
        match join_handle.join() {
            Result::Ok(token) => {
                proof {
                    stamped_tokens = stamped_tokens.join(token.get());
                }
            },
            _ => {
                return ;
            },
        };
        i = i + 1;
    }

See the full verified source for more detail.