Intro
Note: this guide is a work-in-progress.
What’s this guide about?
It’s hard to say exactly what this guide is about. It’s easiest to say that it is primarily about verifying multi-threaded concurrent code in Verus, and in fact, we developed most of this framework with that goal in mind, but these techniques are actually useful for single-threaded code, too. We might also say that it’s about verifying code that needs unsafe features (especially raw pointers and unsafe cells), though again, there are plenty of use-cases where this does not apply.
The unifying theme for the above are programs that require some kind of nontrivial ownership discipline, where different objects that might be “owned independently” need to coordinate somehow. For example:
- Locks need to manage ownership of some underlying resource between multiple clients.
- Reference-counted smart pointers need to coordinate to agree on a reference-count.
- Concurrent data structures (queues, hash tables, and so on) require their client threads to coordinate their access to the data structure.
This kind of nontrivial ownership can be implemented through Verus’s
tokenized_state_machine! utility, and this utility will be the main
tool we’ll learn how to use in this guide.
Who’s this guide for?
Read this if you’re interested in learning how to:
- Verify multi-threaded concurrent code in Verus.
- Verify code that requires “unsafe” code in unverified Rust (e.g., code with raw pointers or unsafe cells)
Or if you just want to know what any of these Verus features are for:
- Verus’s
state_machine!ortokenized_state_machine!macros - Verus’s
trackedvariable mode (“linear ghost state”).
This guide expects general familiarity with Verus, so readers unfamiliar with Verus
should check out the general Verus user guide
first and become proficient at coding within its spec, proof, and exec modes,
using ghost and exec variables.
Further Reading
For a fully comprehensive account, please see Verifying Concurrent Systems Code.
Tokenized State Machines
High-Level Concepts
The approach we follow for each of the examples follows roughly this high-level recipe:
- Consider the program you want to verify.
- Create an “abstraction” of the program as a tokenized state machine.
- Verus will automatically produce for you a bunch of ghost “token types” that make up the tokenized state machine.
- Implement a verified program using the token types
That doesn’t sound too bad, but there’s a bit of an art to it, especially in step (2). To build a proper abstraction, one needs to choose an abstraction which is both abstract enough that it’s easy to prove the relevant properties about, but still concrete enough that it can be properly connected back to the implementation in step (4). Choosing this abstraction requires one to identify which pieces of state need to be in the abstraction, as well as which “tokenization strategy” to use—that’s a concept we’ll be introducing soon.
In the upcoming examples, we’ll look at a variety of scenarios and the techniques we can use to tackle them.
Tutorial by example
In this section, we will walk through a series of increasingly complex examples to illustrate how to use Verus’s tokenized_state_machine! framework to verify concurrent programs.
Counting to 2
Suppose we want to verify a program like the following:
- The main thread instantiates a counter to 0.
- The main thread forks two child threads.
- Each child thread (atomically) increments the counter.
- The main thread joins the two threads (i.e., waits for them to complete).
- The main thread reads the counter.
Our objective: Prove the counter read in the final step has value 2.
// Ordinary Rust code, not Verus
use std::sync::atomic::{AtomicU32, Ordering};
use std::sync::Arc;
use std::thread::spawn;
fn main() {
// Initialize an atomic variable
let atomic = AtomicU32::new(0);
// Put it in an Arc so it can be shared by multiple threads.
let shared_atomic = Arc::new(atomic);
// Spawn a thread to increment the atomic once.
let handle1 = {
let shared_atomic = shared_atomic.clone();
spawn(move || {
shared_atomic.fetch_add(1, Ordering::SeqCst);
})
};
// Spawn another thread to increment the atomic once.
let handle2 = {
let shared_atomic = shared_atomic.clone();
spawn(move || {
shared_atomic.fetch_add(1, Ordering::SeqCst);
})
};
// Wait on both threads. Exit if an unexpected condition occurs.
match handle1.join() {
Result::Ok(()) => {}
_ => {
return;
}
};
match handle2.join() {
Result::Ok(()) => {}
_ => {
return;
}
};
// Load the value, and assert that it should now be 2.
let val = shared_atomic.load(Ordering::SeqCst);
assert!(val == 2);
}We’ll walk through the verification of this snippet, starting with the planning stage.
In general, the verification of a concurrent program will look something like the following:
- Devise an abstraction of the concurrent program. We want an abstraction that is both easy to reason about on its own, but which is “shardable” enough to capture the concurrent execution of the code.
- Formalize the abstraction as a
tokenized_state_machine!system. Use Verus to check that it is well-formed. - Implement the desired code, “annotating” it with ghost tokens provided by
tokenized_state_machine!.
Devising the abstraction
We’ll explain our abstraction using a (possibly overwrought) analogy.
Let’s imagine that the program is taking place in a classroom, with threads and other concepts personified as students.
To start, we’ll use the chalkboard to represent the counter, so we’ll start by writing a 0 on the chalkboard. Then we’ll ask the student council president to watch the chalkboard and make sure that everybody accessing the chalkboard follows the rules.
The rule is simple: the student can walk up to the chalkboard, and if they have a ticket, they can erase the value and increment it by 1. The student council president will stamp the ticket so the same ticket can’t be used again.
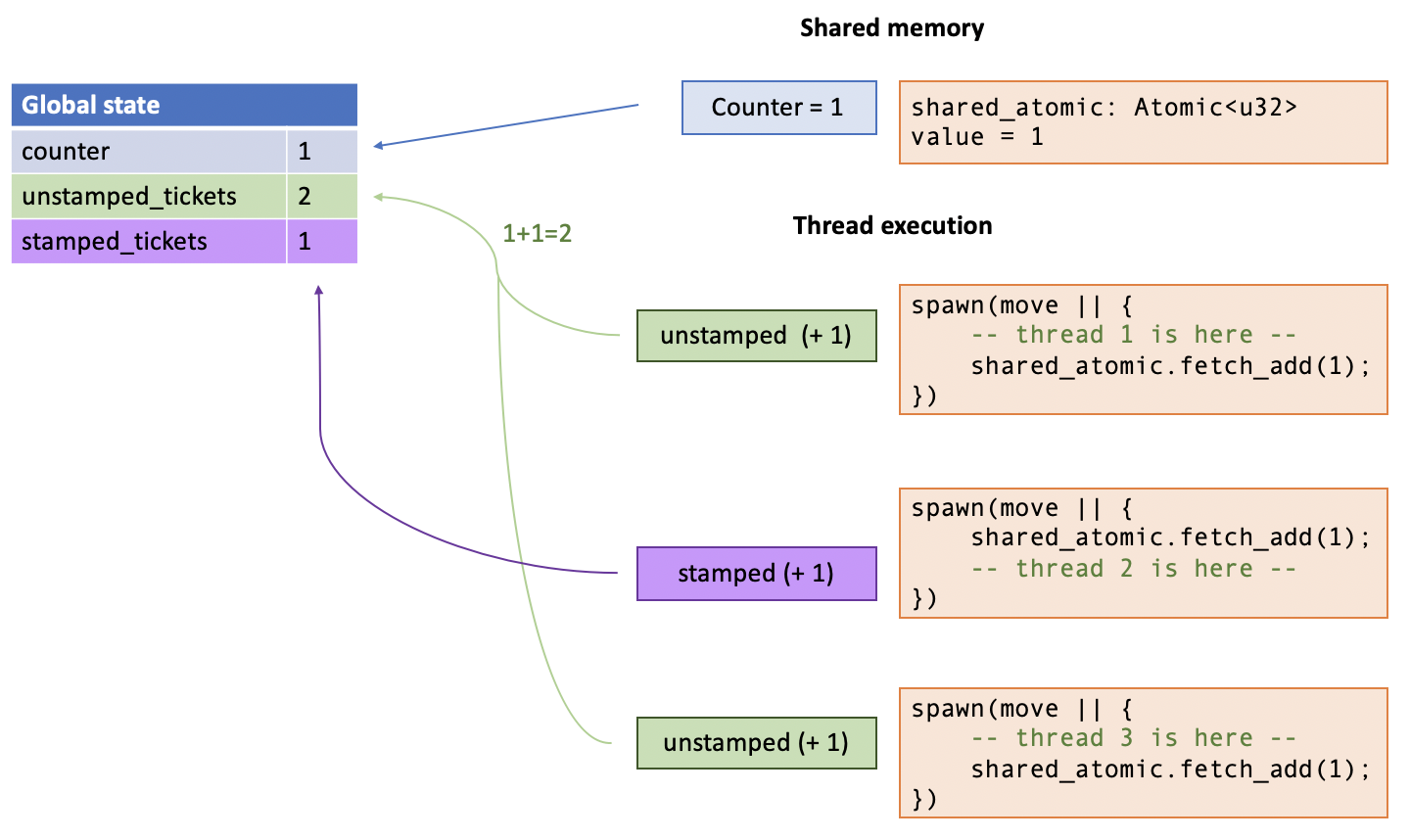
Now: suppose you create two tickets and give them to Alice and Bob. Then, you go take a nap, and when you come back, Alice and Bob both give you two stamped tickets. Now, you go look at the chalkboard. Is it possible to see anything than 2?
No, of course not. It must say 2, since both tickets got stamped, so the chalkboard counter must have incremented 2 times.
There are some implicit assumptions here, naturally. For example, we have to assume that nobody could have forged their own ticket, or their own stamp, or remove stamps…
On the other hand—subject to the players playing by the rules of the game as we laid out—our conclusion that the chalkboard holds the number 2 holds without even making any assumptions about what Alice and Bob did while we were away. For all we know, Alice handed the ticket off to Carol who gave it to Dave, who incremented the counter, who then gave it back to Alice. Maybe Alice and Bob switched tickets. Who knows? It’s all implementation details.
Formalizing the abstraction
It’s time to formalize the above intuition with a tokenized_state_machine!.
The machine is going to have two pieces of state: the counter: int (“the number on the chalkboard”) and the state representing the “tickets”. For the latter, since our example is fixed to the number 2, we’ll represent these as two separate fields, ticket_a: bool and ticket_b: bool, where false means an “unstamped ticket” (i.e., has not incremented the counter) and true represents a “stamped ticket” (i.e., has incremented the counter).
(In the next section we’ll see how to generalize to 2 to n, so we won’t need a separate field for each ticket, but we’ll keep things simple for now.)
Here’s our first (incomplete) attempt at a definition:
tokenized_state_machine!{
X {
fields {
#[sharding(variable)]
pub counter: int,
#[sharding(variable)]
pub ticket_a: bool,
#[sharding(variable)]
pub ticket_b: bool,
}
init!{
initialize() {
init counter = 0; // Initialize “chalkboard” to 0
init ticket_a = false; // Create one “unstamped ticket”
init ticket_b = false; // Create another “unstamped ticket”
}
}
transition!{
do_increment_a() {
require(!pre.ticket_a); // Require the client to provide an “unstamped ticket”
update counter = pre.counter + 1; // Increment the chalkboard counter by 1
update ticket_a = true; // Stamp the ticket
}
}
transition!{
do_increment_b() {
require(!pre.ticket_b); // Require the client to provide an “unstamped ticket”
update counter = pre.counter + 1; // Increment the chalkboard counter by 1
update ticket_b = true; // Stamp the ticket
}
}
readonly!{
finalize() {
require(pre.ticket_a); // Given that both tickets are stamped
require(pre.ticket_b); // ...
assert(pre.counter == 2); // one can conclude the chalkboard value is 2.
}
}
}
}Let’s take this definition one piece at a time. In the fields block, we declared our three states. Note that each one is tagged with a sharding strategy, which tells Verus how to break the state into pieces—we’ll talk about that below. We’ll talk more about the strategies in the next section; right now, all three of our fields use the variable strategy, so we don’t have anything to compare to.
Now we defined four operations on the state machine. The first one is an initialization procedure, named initialize: It lets instantiate the protocol with the counter at 0 and with two unstamped tickets.
The transition do_increment_a lets the client trade in an unstamped ticket for a stamped ticket, while incrementing the counter. The transition do_increment_b is similar, for the ticket_b ticket.
Lastly, we come to the finalize operation. This one is readonly!, as it doesn’t actually update any state. Instead, it lets the client conclude something about the state that we read: just by having the two stamped tickets, we can conclude that the counter value is 2.
Let’s run and see what happens.
error: unable to prove assertion safety condition
--> y.rs:50:17
|
50 | assert(pre.counter == 2);
| ^^^^^^^^^^^^^^^^^^^^^^^^^
error: aborting due to previous error; 1 warning emitted
Uh-oh. Verus wasn’t able to prove the safety condition. Of course not—we didn’t provide any invariant for our system! For all Verus knows, the state {counter: 1, ticket_a: true, ticket_b: true} is valid. Let’s fix this up:
#[invariant]
pub fn main_inv(&self) -> bool {
self.counter == (if self.inc_a { 1 as int } else { 0 }) + (if self.inc_b { 1 as int } else { 0 })
}Our invariant is pretty straightforward: The value of the counter should be equal to the number of stamps. Now, we need to supply stub lemmas to prove that the invariant is preserved by every transition. In this case, Verus completes the proofs easily, so we don’t need to supply any proofs in the lemma bodies to help out Verus.
#[inductive(tr_inc_a)]
fn tr_inc_a_preserves(pre: Self, post: Self) {
}
#[inductive(tr_inc_b)]
fn tr_inc_b_preserves(pre: Self, post: Self) {
}
#[inductive(initialize)]
fn initialize_inv(post: Self) {
}Now that we’ve completed our abstraction, let’s turn towards the implementation.
The Auto-generated Token API
Given a tokenized_state_machine! like the above, Verus will analyze it and produce a series of token types representing pieces of the state, and a series of exchange functions that perform the transitions on the tokens.
(TODO provide instructions for the user to get this information themselves)
Let’s take a look at the tokens that Verus generates here. First, Verus generates an Instance type for instances of the protocol. For the simple state machine here, this doesn’t do very much other than serve as a unique identifier for each instantiation.
#[proof]
#[verifier(unforgeable)]
pub struct Instance { ... }Next, we have token types that represent the actual fields of the state machine. We get one token for each field:
#[proof]
#[verifier(unforgeable)]
pub struct counter {
#[spec] pub instance: X::Instance,
#[spec] pub value: int,
}
#[proof]
#[verifier(unforgeable)]
pub struct ticket_a {
#[spec] pub instance: X::Instance,
#[spec] pub value: bool,
}
#[proof]
#[verifier(unforgeable)]
pub struct ticket_b {
#[spec] pub instance: X::Instance,
#[spec] pub value: bool,
}For example, ownership of a token X::counter { instance: inst, value: 5 } represents proof that the instance inst of the protocol currently has its counter state set to 5. With all three tokens for a given instance taken altogether, we recover the full state.
Now, let’s take a look at the exchange functions. We start with X::Instance::initialize, generated from our declared initialize operation. This function returns a fresh instance of the protocol (X::Instance) and tokens for each field (X::counter, X::ticket_a, and X::ticket_b) all initialized to the values as we declared them (0, false, and false).
impl Instance {
// init!{
// initialize() {
// init counter = 0;
// init ticket_a = false;
// init ticket_b = false;
// }
// }
#[proof]
#[verifier(returns(proof))]
pub fn initialize() -> (X::Instance, X::counter, X::ticket_a, X::ticket_b) {
ensures(|tmp_tuple: (X::Instance, X::counter, X::ticket_a, X::ticket_b)| {
[{
let (instance, token_counter, token_ticket_a, token_ticket_b) = tmp_tuple;
(equal(token_counter.instance, instance))
&& (equal(token_ticket_a.instance, instance))
&& (equal(token_ticket_b.instance, instance))
&& (equal(token_counter.value, 0)) // init counter = 0;
&& (equal(token_ticket_a.value, false)) // init ticket_a = false;
&& (equal(token_ticket_b.value, false)) // init ticket_b = false;
}]
});
...
}Next, the function for the do_increment_a transition. Note that enabling condition in the user’s declared transition
becomes a precondition for calling of do_increment_a. The exchange function takes a X::counter and X::ticket_a token as input,
and since the transition modifies both fields, the exchange function takes the tokens as &mut.
Also note, crucially, that it does not take a X::ticket_b token at all because the transition doesn’t depend on the ticket_b field.
The transition can be performed entirely without reference to it.
// transition!{
// do_increment_a() {
// require(!pre.ticket_a);
// update counter = pre.counter + 1;
// update ticket_a = true;
// }
// }
#[proof]
pub fn do_increment_a(
#[proof] &self,
#[proof] token_counter: &mut X::counter,
#[proof] token_ticket_a: &mut X::ticket_a,
) {
requires([
equal(old(token_counter).instance, (*self)),
equal(old(token_ticket_a).instance, (*self)),
(!old(token_ticket_a).value), // require(!pre.ticket_a)
]);
ensures([
equal(token_counter.instance, (*self)),
equal(token_ticket_a.instance, (*self)),
equal(token_counter.value, old(token_counter).value + 1), // update counter = pre.counter + 1
equal(token_ticket_a.value, true), // update ticket_a = true
]);
...
}The function for the do_increment_b transition is similar:
// transition!{
// do_increment_b() {
// require(!pre.ticket_b);
// update counter = pre.counter + 1;
// update ticket_b = true;
// }
// }
#[proof]
pub fn do_increment_b(
#[proof] &self,
#[proof] token_counter: &mut X::counter,
#[proof] token_ticket_b: &mut X::ticket_b,
) {
requires([
equal(old(token_counter).instance, (*self)),
equal(old(token_ticket_b).instance, (*self)),
(!old(token_ticket_b).value), // require(!pre.ticket_b)
]);
ensures([
equal(token_counter.instance, (*self)),
equal(token_ticket_b.instance, (*self)),
equal(token_counter.value, old(token_counter).value + 1), // update counter = pre.counter + 1
equal(token_ticket_b.value, true), // update ticket_b = true
]);
...
}Finally, we come to the finalize operation. Again this is a “no-op” transition that doesn’t update any fields, so the generated exchange method takes the tokens as readonly parameters (non-mutable borrows). Here, we observe that the assert becomes a post-condition, that is, by performing this operation, though it does not update any state, causes us to learn something about that state.
// readonly!{
// finalize() {
// require(pre.ticket_a);
// require(pre.ticket_b);
// assert(pre.counter == 2);
// }
// }
#[proof]
pub fn finalize(
#[proof] &self,
#[proof] token_counter: &X::counter,
#[proof] token_ticket_a: &X::ticket_a,
#[proof] token_ticket_b: &X::,
) {
requires([
equal(token_counter.instance, (*self)),
equal(token_ticket_a.instance, (*self)),
equal(token_ticket_b.instance, (*self)),
(token_ticket_a.value), // require(pre.ticket_a)
(token_ticket_b.value), // require(pre.ticket_b)
]);
ensures([token_counter.value == 2]); // assert(pre.counter == 2)
...
}
}Writing the verified implementation
To verify the implementation, our plan is to instantiate this ghost protocol and associate
the counter field of the protocol to the atomic memory location we use in our code.
To do this, we’ll use the Verus library atomic_ghost.
Specifically, we’ll use the type atomic_ghost::AtomicU32<X::counter>.
This is a wrapper around an AtomicU32 location which associates it to a tracked
ghost token X::counter.
More specifically, all threads will share this global state:
struct_with_invariants!{
pub struct Global {
// An AtomicU32 that matches with the `counter` field of the ghost protocol.
pub atomic: AtomicU32<_, X::counter, _>,
// The instance of the protocol that the `counter` is part of.
pub instance: Tracked<X::Instance>,
}
spec fn wf(&self) -> bool {
// Specify the invariant that should hold on the AtomicU32<X::counter>.
// Specifically the ghost token (`g`) should have
// the same value as the atomic (`v`).
// Furthermore, the ghost token should have the appropriate `instance`.
invariant on atomic with (instance) is (v: u32, g: X::counter) {
g.instance_id() == instance@.id()
&& g.value() == v as int
}
}
}Note that we track instance as a separate field. This ensures that all threads agree
on which instance of the protocol they are running.
(Keep in mind that whenever we perform a transition on the ghost tokens, all the tokens have to have the same instance. Why does Verus enforce restriction? Because if it did not, then the programmer could instantiate two instances of the protocol, the mix-and-match to get into an invalid state. For example, they could increment the counter twice, using up both “tickets” of that instance, and then use the ticket of another instance to increment it a third time.)
TODO finish writing the explanation
Counting to 2, unverified Rust source
// Ordinary Rust code, not Verus
use std::sync::atomic::{AtomicU32, Ordering};
use std::sync::Arc;
use std::thread::spawn;
fn main() {
// Initialize an atomic variable
let atomic = AtomicU32::new(0);
// Put it in an Arc so it can be shared by multiple threads.
let shared_atomic = Arc::new(atomic);
// Spawn a thread to increment the atomic once.
let handle1 = {
let shared_atomic = shared_atomic.clone();
spawn(move || {
shared_atomic.fetch_add(1, Ordering::SeqCst);
})
};
// Spawn another thread to increment the atomic once.
let handle2 = {
let shared_atomic = shared_atomic.clone();
spawn(move || {
shared_atomic.fetch_add(1, Ordering::SeqCst);
})
};
// Wait on both threads. Exit if an unexpected condition occurs.
match handle1.join() {
Result::Ok(()) => {}
_ => {
return;
}
};
match handle2.join() {
Result::Ok(()) => {}
_ => {
return;
}
};
// Load the value, and assert that it should now be 2.
let val = shared_atomic.load(Ordering::SeqCst);
assert!(val == 2);
}Counting to 2, verified source
use verus_builtin::*;
use verus_builtin_macros::*;
use verus_state_machines_macros::tokenized_state_machine;
use std::sync::Arc;
use vstd::atomic_ghost::*;
use vstd::modes::*;
use vstd::prelude::*;
use vstd::thread::*;
use vstd::{pervasive::*, *};
verus! {
tokenized_state_machine!(
X {
fields {
#[sharding(variable)]
pub counter: int,
#[sharding(variable)]
pub inc_a: bool,
#[sharding(variable)]
pub inc_b: bool,
}
#[invariant]
pub fn main_inv(&self) -> bool {
self.counter == (if self.inc_a { 1 as int } else { 0 }) + (if self.inc_b { 1 as int } else { 0 })
}
init!{
initialize() {
init counter = 0;
init inc_a = false;
init inc_b = false;
}
}
transition!{
tr_inc_a() {
require(!pre.inc_a);
update counter = pre.counter + 1;
update inc_a = true;
}
}
transition!{
tr_inc_b() {
require(!pre.inc_b);
update counter = pre.counter + 1;
update inc_b = true;
}
}
property!{
increment_will_not_overflow_u32() {
assert 0 <= pre.counter < 0xffff_ffff;
}
}
property!{
finalize() {
require(pre.inc_a);
require(pre.inc_b);
assert pre.counter == 2;
}
}
#[inductive(tr_inc_a)]
fn tr_inc_a_preserves(pre: Self, post: Self) {
}
#[inductive(tr_inc_b)]
fn tr_inc_b_preserves(pre: Self, post: Self) {
}
#[inductive(initialize)]
fn initialize_inv(post: Self) {
}
}
);
struct_with_invariants!{
pub struct Global {
// An AtomicU32 that matches with the `counter` field of the ghost protocol.
pub atomic: AtomicU32<_, X::counter, _>,
// The instance of the protocol that the `counter` is part of.
pub instance: Tracked<X::Instance>,
}
spec fn wf(&self) -> bool {
// Specify the invariant that should hold on the AtomicU32<X::counter>.
// Specifically the ghost token (`g`) should have
// the same value as the atomic (`v`).
// Furthermore, the ghost token should have the appropriate `instance`.
invariant on atomic with (instance) is (v: u32, g: X::counter) {
g.instance_id() == instance@.id()
&& g.value() == v as int
}
}
}
fn main() {
// Initialize protocol
let tracked (
Tracked(instance),
Tracked(counter_token),
Tracked(inc_a_token),
Tracked(inc_b_token),
) = X::Instance::initialize();
// Initialize the counter
let tr_instance: Tracked<X::Instance> = Tracked(instance.clone());
let atomic = AtomicU32::new(Ghost(tr_instance), 0, Tracked(counter_token));
let global = Global { atomic, instance: Tracked(instance.clone()) };
let global_arc = Arc::new(global);
// Spawn threads
// Thread 1
let global_arc1 = global_arc.clone();
let join_handle1 = spawn(
(move || -> (new_token: Tracked<X::inc_a>)
ensures
new_token@.instance_id() == instance.id() && new_token@.value() == true,
{
// `inc_a_token` is moved into the closure
let tracked mut token = inc_a_token;
let globals = &*global_arc1;
let _ =
atomic_with_ghost!(&globals.atomic => fetch_add(1);
ghost c => {
globals.instance.borrow().increment_will_not_overflow_u32(&c);
globals.instance.borrow().tr_inc_a(&mut c, &mut token); // atomic increment
}
);
Tracked(token)
}),
);
// Thread 2
let global_arc2 = global_arc.clone();
let join_handle2 = spawn(
(move || -> (new_token: Tracked<X::inc_b>)
ensures
new_token@.instance_id() == instance.id() && new_token@.value() == true,
{
// `inc_b_token` is moved into the closure
let tracked mut token = inc_b_token;
let globals = &*global_arc2;
let _ =
atomic_with_ghost!(&globals.atomic => fetch_add(1);
ghost c => {
globals.instance.borrow().increment_will_not_overflow_u32(&mut c);
globals.instance.borrow().tr_inc_b(&mut c, &mut token); // atomic increment
}
);
Tracked(token)
}),
);
// Join threads
let tracked inc_a_token;
match join_handle1.join() {
Result::Ok(token) => {
proof {
inc_a_token = token.get();
}
},
_ => {
return ;
},
};
let tracked inc_b_token;
match join_handle2.join() {
Result::Ok(token) => {
proof {
inc_b_token = token.get();
}
},
_ => {
return ;
},
};
// Join threads, load the atomic again
let global = &*global_arc;
let x =
atomic_with_ghost!(&global.atomic => load();
ghost c => {
instance.finalize(&c, &inc_a_token, &inc_b_token);
}
);
assert(x == 2);
}
} // verus!Counting to n
Let’s now generalize the previous exercise from using a fixed number of threads (2) to using an an arbitrary number of threads. Specifically, we’ll verify the equivalent of the following Rust program:
- The main thread instantiates a counter to 0.
- The main thread forks
num_threadschild threads.- Each child thread (atomically) increments the counter.
- The main thread joins all the threads (i.e., waits for them to complete).
- The main thread reads the counter.
Our objective: Prove the counter read in the final step has value num_threads.
// Ordinary Rust code, not Verus
use std::sync::atomic::{AtomicU32, Ordering};
use std::sync::Arc;
use std::thread::spawn;
fn do_count(num_threads: u32) {
// Initialize an atomic variable
let atomic = AtomicU32::new(0);
// Put it in an Arc so it can be shared by multiple threads.
let shared_atomic = Arc::new(atomic);
// Spawn `num_threads` threads to increment the atomic once.
let mut handles = Vec::new();
for _i in 0..num_threads {
let handle = {
let shared_atomic = shared_atomic.clone();
spawn(move || {
shared_atomic.fetch_add(1, Ordering::SeqCst);
})
};
handles.push(handle);
}
// Wait on all threads. Exit if an unexpected condition occurs.
for handle in handles.into_iter() {
match handle.join() {
Result::Ok(()) => {}
_ => {
return;
}
};
}
// Load the value, and assert that it should now be `num_threads`.
let val = shared_atomic.load(Ordering::SeqCst);
assert!(val == num_threads);
}
fn main() {
do_count(20);
}Verified implementation
We’ll build off the previous exercise here, so make sure you’re familiar with that one first.
Our first step towards verifying the generalized program
is to update the tokenized_state_machine from the earlier example.
Recall that in that example, we had two boolean fields, inc_a and inc_b,
to represent the two tickets.
This time, we will merely maintain counts of the number of tickets:
we’ll have one field for the number of unstamped tickets and one for the number
of stamped tickets.
Let’s start with the updated state machine, but ignore the tokenization aspect for now. Here’s the updated state machine as an atomic state machine:
state_machine! {
X {
fields {
pub num_threads: nat,
pub counter: int,
pub unstamped_tickets: nat,
pub stamped_tickets: nat,
}
#[invariant]
pub fn main_inv(&self) -> bool {
self.counter == self.stamped_tickets
&& self.stamped_tickets + self.unstamped_tickets == self.num_threads
}
init!{
initialize(num_threads: nat) {
init num_threads = num_threads;
init counter = 0;
init unstamped_tickets = num_threads;
init stamped_tickets = 0;
}
}
transition!{
tr_inc() {
// Replace a single unstamped ticket with a stamped ticket
require(pre.unstamped_tickets >= 1);
update unstamped_tickets = (pre.unstamped_tickets - 1) as nat;
update stamped_tickets = pre.stamped_tickets + 1;
assert(pre.counter < pre.num_threads);
update counter = pre.counter + 1;
}
}
property!{
finalize() {
require(pre.stamped_tickets >= pre.num_threads);
assert(pre.counter == pre.num_threads);
}
}
// ... invariant proofs here
}
}Note that we added a new field, num_threads, and we replaced inc_a and inc_b with unstamped_tickets and stampted_tickets.
Now, let’s talk about the tokenization. In the previous example, all of our fields used the variable strategy, but we never got a chance to talk about what that meant. Let’s now see some of the other strategies.
For our new program, we will need to make two changes.
The constant strategy
First, the num_threads can be marked as a constant, since this value is really just
a parameter to the protocol, and will be fixed for any given instance of it.
By marking it constant, we won’t get a token for it, but instead the value will be available
from the shared Instance object.
The count strategy
This change is far more subtle. The key problem we need to solve is that the “tickets” need
to be spread across multiple threads. However, if unstamped_tickets and stamped_tickets
were marked as variable then we would only get one token for each field.
Recall our physical analogy with the tickets and the chalkboard (used for the counter field),
and compare: there’s actually something fundamentally different about the tickets
and the chalkboard, which is that the tickets are actually a count of something.
Think of it this way:
- If Alice has 3 tickets, and Bob has 2 tickets, then together they have 5 tickets.
- If Alice has a chalkboard with the number 3 written on it, and Bob has a chalkboard with the number 2 on it, then together do they have a chalkboard with the number 5 written on it?
- No! They just have two chalkboards with 2 and 3 written on them. In fact, in our scenario, we aren’t even supposed to have more than 1 chalkboard anyway. Alice and Bob are in an invalid state here.
We need a way to mark this distinction, that is, we need a way to be able to say,
“this field is a value on a chalkboard” versus “the field indicates the number of some thing”.
The variable strategy we have been using until now is the former;
the newly introduce count strategy is the latter.
Thus, we need to use the count strategy for the ticket fields.
We need to mark the ticket fields as being a “count” of something, and this is exactly
what the count strategy is for. Rather than having exactly one token for the
field value, the count strategy will make it so that the field value is
the sum total of all the tokens in the system
associated with that field. (However, this new flexibility will come
with some restrictions, as we will see.)
Here, we can visualize how the ghost tokens are spread throughout the running system, and how they relate to the global state:
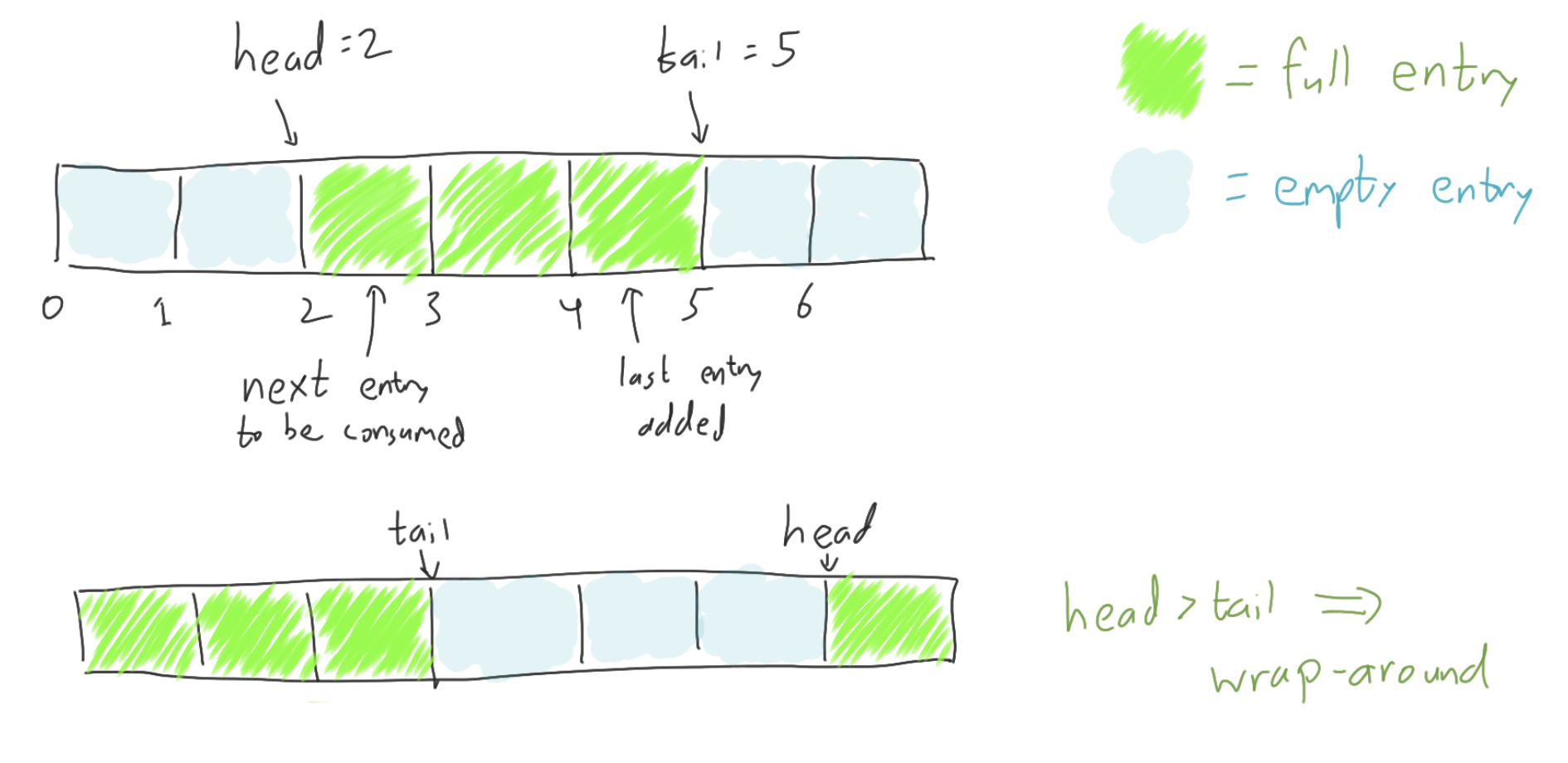
In this scenario, we have three threads, all of which are currenlty executing,
where thread 2 has incremented the counter, but threads 1 and 3 have not.
Thus, threads 1 and 3 each have an “unstamped ticket” token,
while thread 2 has a “stamped ticket” token.
The abstract global state, then, has
unstamped_tickets == 2 and stamped_tickets == 1.
Building the new tokenized_state_machine
First, we mark the fields with the appropriate strategies, as we discussed:
tokenized_state_machine!{
X {
fields {
#[sharding(constant)]
pub num_threads: nat,
#[sharding(variable)]
pub counter: int,
#[sharding(count)]
pub unstamped_tickets: nat,
#[sharding(count)]
pub stamped_tickets: nat,
}Just by marking the strategies, we can already see how it impacts the generated token code.
Let’s look at unstamped_tickets (the stamped_tickets is, of course, similar):
// Code auto-generated by tokenized_state_machine! macro
#[proof]
#[verifier(unforgeable)]
pub struct unstamped_tickets {
#[spec] pub instance: Instance,
#[spec] pub value: nat,
}
impl unstamped_tickets {
#[proof]
#[verifier(returns(proof))]
pub fn join(#[proof] self, #[proof] other: Self) -> Self {
requires(equal(self.instance, other.instance));
ensures(|s: Self| {
equal(s.instance, self.instance)
&& equal(s.value, self.value + other.value)
});
// ...
}
#[proof]
#[verifier(returns(proof))]
pub fn split(#[proof] self, #[spec] i: nat) -> (Self, Self) {
requires(i <= self.value);
ensures(|s: (Self, Self)| {
equal(s.0.instance, self.instance)
&& equal(s.1.instance, self.instance)
&& equal(s.0.value, i)
&& equal(s.1.value, self.value - i)
});
// ...
}
}The token type, unstamped_tickets comes free with 2 associated methods,
join and split. First, join lets us take two tokens with an associate count and
merge them together to get a single token with the combined count value;
meanwhile, split goes the other way.
So for example, when we start out with a single token of count num_threads, we can
split into num_threads tokens, each with count 1.
Now, let’s move on to the rest of the system.
Our invariant and the initialization routine will be identical to before.
(In general, init statements are used for all sharding strategies.
The sharding strategies might affect the token method that gets generated, but the
init! definition itself will remain the same.)
#[invariant]
pub fn main_inv(&self) -> bool {
self.counter == self.stamped_tickets
&& self.stamped_tickets + self.unstamped_tickets == self.num_threads
}
init!{
initialize(num_threads: nat) {
init num_threads = num_threads;
init counter = 0;
init unstamped_tickets = num_threads;
init stamped_tickets = 0;
}
}The tr_inc definition is where it gets interesting. Let’s take a closer look at the definition
we gave earlier:
transition!{
tr_inc() {
// Replace a single unstamped ticket with a stamped ticket
require(pre.unstamped_tickets >= 1);
update unstamped_tickets = pre.unstamped_tickets - 1;
update stamped_tickets = pre.stamped_tickets + 1;
assert(pre.counter < pre.num_threads);
update counter = pre.counter + 1;
}
} There’s a problem here, which is that the operation directly accesses pre.unstamped_tickets
and writes to the same field with an update statement, and likewise for the
stamped_tickets field. Because these fields are marked with the count strategy,
Verus will reject this definition.
So why does Verus have to reject it? Keep in mind that whatever definition we give here, Verus has to be able to create a transition definition that works in the tokenized view of the world. In any tokenized transition, the tokens that serve as input must by themselves be able to justify the validity of the transition being performed.
Unfortunately, this justification is impossible when we are using the count strategy.
When the field is tokenized according to the count strategy,
there is no way for a client to produce a set of
tokens that definitively determines the value of the unstamped_tickets field in the global state machine.
For instance, suppose the client provides three such tokens; this does not necessarily means
that pre.unstamped_tickets is equal to 3! Rather, there might be other tokens
elsewhere in the system held on by other threads, so all we can justify from the existence
of those tokens is that pre.unstamped_tickets is greater than or equal to 3.
Thus, Verus demands that we do not read or write to the field arbitrarily.
Effectively, we can only perform operations that look like one of the following for a count-strategy field:
- Require the field’s value to be greater than some natural number
- Subtract a natural number
- Add a natural number
Luckily, we can see that the transition from earlier only does these allowed things. To get Verus to accept it, we only need to write the transition using a special syntax so that it can identify the patterns involved.
transition!{
tr_inc() {
// Equivalent to:
// require(pre.unstamped_tickets >= 1);
// update unstampted_tickets = pre.unstamped_tickets - 1
// (In any `remove` statement, the `>=` condition is always implicit.)
remove unstamped_tickets -= (1);
// Equivalent to:
// update stamped_tickets = pre.stamped_tickets + 1
add stamped_tickets += (1);
// These still use ordinary 'update' syntax, because `pre.counter`
// uses the `variable` sharding strategy.
assert(pre.counter < pre.num_threads);
update counter = pre.counter + 1;
}
}Generally, a remove corresponds to destroying a token, while add corresponds to creating a token. Thus the generated exchange function takes an unstamped_tickets token as input
and gives a stamped_tickets token as output.
Ultimately, thus, it exchanges an unstamped ticket for a stamped ticket.
// Code auto-generated by tokenized_state_machine! macro
#[proof]
#[verifier(returns(proof))]
pub fn tr_inc(
#[proof] &self,
#[proof] token_counter: &mut counter,
#[proof] token_0_unstamped_tickets: unstamped_tickets, // input (destroyed)
) -> stamped_tickets // output (created)
{
requires([
equal(old(token_counter).instance, (*self)),
equal(token_0_unstamped_tickets.instance, (*self)),
equal(token_0_unstamped_tickets.value, 1), // remove unstamped_tickets -= (1);
]);
ensures(|token_1_stamped_tickets: stamped_tickets| {
[
equal(token_counter.instance, (*self)),
equal(token_1_stamped_tickets.instance, (*self)),
equal(token_1_stamped_tickets.value, 1), // add stamped_tickets += (1);
(old(token_counter).value < (*self).num_threads()), // assert(pre.counter < pre.num_threads);
equal(token_counter.value, old(token_counter).value + 1), // update counter = pre.counter + 1;
]
});
// ...
}The finalize transition needs to be updated in a similar way:
property!{
finalize() {
// Equivalent to:
// require(pre.unstamped_tickets >= pre.num_threads);
have stamped_tickets >= (pre.num_threads);
assert(pre.counter == pre.num_threads);
}
}The have statement is similar to remove, except that it doesn’t do the remove.
It just requires the client to provide tokens counting in total at least pre.num_threads here,
but it doesn’t consume them.
Again, notice that the condition we have to write is equivalent to a >= condition.
We can’t just require that stamped_tickets == pre.num_threads.
(Incidentally, it does happen to be the case that pre.stamped_tickets >= pre.num_threads
implies that pre.stamped_tickets == pre.num_threads. This implication follows
from the the invariant, but it isn’t something we know a priori.
Therefore, it is still the case that we have to write the transition with the weaker requirement
that pre.stamped_tickets >= pre.num_threads. The safety proof will then deduce that
pre.stamped_tickets == pre.num_threads from the invariant, and then deduce that
pre.counter == pre.num_threads, which is what we really want in the end.)
// Code auto-generated by tokenized_state_machine! macro
#[proof]
pub fn finalize(
#[proof] &self,
#[proof] token_counter: &counter,
#[proof] token_0_stamped_tickets: &stamped_tickets,
) {
requires([
equal(token_counter.instance, (*self)),
equal(token_0_stamped_tickets.instance, (*self)),
equal(token_0_stamped_tickets.value, (*self).num_threads()), // have stamped_tickets >= (pre.num_threads);
]);
ensures([(token_counter.value == (*self).num_threads())]); // assert(pre.counter == pre.num_threads);
// ...
}Verified Implementation
The implementation of a thread’s action hasn’t change much from before. The only difference
is that we are now
exchanging an unstamped_ticket for a stamped_ticket, rather than updating a
boolean field.
Perhaps more interesting now is the main function which does the spawning and joining.
It has to spawn threads in a loop. Note that we start with a stamped_tokens count of
num_threads. Each iteration of the loop, we “peel off” a single ticket (1 unit’s worth)
and pass it into the newly spawned thread.
// Spawn threads
let mut join_handles: Vec<JoinHandle<Tracked<X::stamped_tickets>>> = Vec::new();
let mut i = 0;
while i < num_threads
invariant
0 <= i,
i <= num_threads,
unstamped_tokens.count() + i == num_threads,
unstamped_tokens.instance_id() == instance.id(),
join_handles@.len() == i as int,
forall|j: int, ret|
0 <= j && j < i ==> join_handles@.index(j).predicate(ret) ==>
ret@.instance_id() == instance.id()
&& ret@.count() == 1,
(*global_arc).wf(),
(*global_arc).instance@ === instance,
{
let tracked unstamped_token;
proof {
unstamped_token = unstamped_tokens.split(1 as nat);
}
let global_arc = global_arc.clone();
let join_handle = spawn(
(move || -> (new_token: Tracked<X::stamped_tickets>)
ensures
new_token@.instance_id() == instance.id(),
new_token@.count() == 1,
{
let tracked unstamped_token = unstamped_token;
let globals = &*global_arc;
let tracked stamped_token;
let _ =
atomic_with_ghost!(
&global_arc.atomic => fetch_add(1);
update prev -> next;
returning ret;
ghost c => {
stamped_token =
global_arc.instance.borrow().tr_inc(&mut c, unstamped_token);
}
);
Tracked(stamped_token)
}),
);
join_handles.push(join_handle);
i = i + 1;
}Then, when we join the threads, we do the opposite: we collect the “stamped ticket” tokens
until we have collected all num_threads of them.
// Join threads
let mut i = 0;
while i < num_threads
invariant
0 <= i,
i <= num_threads,
stamped_tokens.count() == i,
stamped_tokens.instance_id() == instance.id(),
join_handles@.len() as int + i as int == num_threads,
forall|j: int, ret|
0 <= j && j < join_handles@.len() ==>
#[trigger] join_handles@.index(j).predicate(ret) ==>
ret@.instance_id() == instance.id()
&& ret@.count() == 1,
(*global_arc).wf(),
(*global_arc).instance@ === instance,
{
let join_handle = join_handles.pop().unwrap();
match join_handle.join() {
Result::Ok(token) => {
proof {
stamped_tokens.join(token.get());
}
},
_ => {
return ;
},
};
i = i + 1;
}See the full verified source for more detail.
Counting to n, unverified Rust source
// Ordinary Rust code, not Verus
use std::sync::atomic::{AtomicU32, Ordering};
use std::sync::Arc;
use std::thread::spawn;
fn do_count(num_threads: u32) {
// Initialize an atomic variable
let atomic = AtomicU32::new(0);
// Put it in an Arc so it can be shared by multiple threads.
let shared_atomic = Arc::new(atomic);
// Spawn `num_threads` threads to increment the atomic once.
let mut handles = Vec::new();
for _i in 0..num_threads {
let handle = {
let shared_atomic = shared_atomic.clone();
spawn(move || {
shared_atomic.fetch_add(1, Ordering::SeqCst);
})
};
handles.push(handle);
}
// Wait on all threads. Exit if an unexpected condition occurs.
for handle in handles.into_iter() {
match handle.join() {
Result::Ok(()) => {}
_ => {
return;
}
};
}
// Load the value, and assert that it should now be `num_threads`.
let val = shared_atomic.load(Ordering::SeqCst);
assert!(val == num_threads);
}
fn main() {
do_count(20);
}Counting to n, verified source
use verus_state_machines_macros::tokenized_state_machine;
use std::sync::Arc;
use vstd::atomic_ghost::*;
use vstd::modes::*;
use vstd::prelude::*;
use vstd::thread::*;
use vstd::{pervasive::*, prelude::*, *};
verus! {
tokenized_state_machine!{
X {
fields {
#[sharding(constant)]
pub num_threads: nat,
#[sharding(variable)]
pub counter: int,
#[sharding(count)]
pub unstamped_tickets: nat,
#[sharding(count)]
pub stamped_tickets: nat,
}
#[invariant]
pub fn main_inv(&self) -> bool {
self.counter == self.stamped_tickets
&& self.stamped_tickets + self.unstamped_tickets == self.num_threads
}
init!{
initialize(num_threads: nat) {
init num_threads = num_threads;
init counter = 0;
init unstamped_tickets = num_threads;
init stamped_tickets = 0;
}
}
transition!{
tr_inc() {
// Equivalent to:
// require(pre.unstamped_tickets >= 1);
// update unstampted_tickets = pre.unstamped_tickets - 1
// (In any `remove` statement, the `>=` condition is always implicit.)
remove unstamped_tickets -= (1);
// Equivalent to:
// update stamped_tickets = pre.stamped_tickets + 1
add stamped_tickets += (1);
// These still use ordinary 'update' syntax, because `pre.counter`
// uses the `variable` sharding strategy.
assert(pre.counter < pre.num_threads);
update counter = pre.counter + 1;
}
}
property!{
finalize() {
// Equivalent to:
// require(pre.unstamped_tickets >= pre.num_threads);
have stamped_tickets >= (pre.num_threads);
assert(pre.counter == pre.num_threads);
}
}
#[inductive(initialize)]
fn initialize_inductive(post: Self, num_threads: nat) { }
#[inductive(tr_inc)]
fn tr_inc_preserves(pre: Self, post: Self) {
}
}
}
struct_with_invariants!{
pub struct Global {
pub atomic: AtomicU32<_, X::counter, _>,
pub instance: Tracked<X::Instance>,
}
spec fn wf(&self) -> bool {
invariant on atomic with (instance) is (v: u32, g: X::counter) {
g.instance_id() == instance@.id()
&& g.value() == v as int
}
predicate {
self.instance@.num_threads() < 0x100000000
}
}
}
fn do_count(num_threads: u32) {
// Initialize protocol
let tracked (
Tracked(instance),
Tracked(counter_token),
Tracked(unstamped_tokens),
Tracked(stamped_tokens),
) = X::Instance::initialize(num_threads as nat);
// Initialize the counter
let tracked_instance = Tracked(instance.clone());
let atomic = AtomicU32::new(Ghost(tracked_instance), 0, Tracked(counter_token));
let global = Global { atomic, instance: tracked_instance };
let global_arc = Arc::new(global);
// Spawn threads
let mut join_handles: Vec<JoinHandle<Tracked<X::stamped_tickets>>> = Vec::new();
let mut i = 0;
while i < num_threads
invariant
0 <= i,
i <= num_threads,
unstamped_tokens.count() + i == num_threads,
unstamped_tokens.instance_id() == instance.id(),
join_handles@.len() == i as int,
forall|j: int, ret|
0 <= j && j < i ==> join_handles@.index(j).predicate(ret) ==>
ret@.instance_id() == instance.id()
&& ret@.count() == 1,
(*global_arc).wf(),
(*global_arc).instance@ === instance,
{
let tracked unstamped_token;
proof {
unstamped_token = unstamped_tokens.split(1 as nat);
}
let global_arc = global_arc.clone();
let join_handle = spawn(
(move || -> (new_token: Tracked<X::stamped_tickets>)
ensures
new_token@.instance_id() == instance.id(),
new_token@.count() == 1,
{
let tracked unstamped_token = unstamped_token;
let globals = &*global_arc;
let tracked stamped_token;
let _ =
atomic_with_ghost!(
&global_arc.atomic => fetch_add(1);
update prev -> next;
returning ret;
ghost c => {
stamped_token =
global_arc.instance.borrow().tr_inc(&mut c, unstamped_token);
}
);
Tracked(stamped_token)
}),
);
join_handles.push(join_handle);
i = i + 1;
}
// Join threads
let mut i = 0;
while i < num_threads
invariant
0 <= i,
i <= num_threads,
stamped_tokens.count() == i,
stamped_tokens.instance_id() == instance.id(),
join_handles@.len() as int + i as int == num_threads,
forall|j: int, ret|
0 <= j && j < join_handles@.len() ==>
#[trigger] join_handles@.index(j).predicate(ret) ==>
ret@.instance_id() == instance.id()
&& ret@.count() == 1,
(*global_arc).wf(),
(*global_arc).instance@ === instance,
{
let join_handle = join_handles.pop().unwrap();
match join_handle.join() {
Result::Ok(token) => {
proof {
stamped_tokens.join(token.get());
}
},
_ => {
return ;
},
};
i = i + 1;
}
let global = &*global_arc;
let x =
atomic_with_ghost!(&global.atomic => load();
ghost c => {
instance.finalize(&c, &stamped_tokens);
}
);
assert(x == num_threads);
}
fn main() {
do_count(20);
}
} // verus!Single-Producer, Single-Consumer queue, tutorial
Here, we’ll walk through an example of verifying a single-producer, single-consumer queue. Specifically, we’re interested in the following interface:
type Producer<T>
type Consumer<T>
impl<T> Producer<T> {
pub fn enqueue(&mut self, t: T)
}
impl<T> Consumer<T> {
pub fn dequeue(&mut self) -> T
}
pub fn new_queue<T>(len: usize) -> (Producer<T>, Consumer<T>)Unverified implementation
First, let’s discuss the reference implementation, written in ordinary Rust, that we’re going to be verifying (an equivalent of).
The implementation is going to use a ring buffer of fixed length len,
with a head and a tail pointer,
with the producer adding new entries to the tail and
the consumer popping old entries from the head.
Thus the entries in the range [head, tail) will always be full.
If head == tail then the ring buffer will be considered empty,
and if head > tail, then the interval wraps around.
The crucial design choice is what data structure to use for the buffer itself. The key requirements of the buffer are:
- A reference to the buffer memory must be shared between threads (the producer and the consumer)
- Each entry might or might not store a valid
Telement at any given point in time.
In our unverified Rust implementation, we’ll let each entry be an UnsafeCell.
The UnsafeCell gives us interior mutability, so that we can
read and write the contents from multiple threads without
any extra metadata associated to each entry. UnsafeCell is of course, as the name suggests, unsafe, meaning that it’s up to the programmer to ensure the all these reads and writes are performed safely. For our purposes, safely mostly means data-race-free.
More specifically, we’ll use an UnsafeCell<MaybeUninit<T>> for each entry.
The MaybeUninit
allows for the possibility that an entry is uninitialized. Like with UnsafeCell, there are no
runtime safety checks, so it is entirely upon the programmer to make sure it doesn’t try to read
from the entry when it’s uninitialized.
Hang on, why not just use
Option<T>?To be safer, we could use an
Option<T>instead ofMaybeUninit<T>, but we are already doing low-level data management anyway, and anOption<T>would be less efficient. In particular, if we used anOption<T>, then popping an entry out of the queue would mean we having to writeNoneback into the queue to signify its emptiness. WithMaybeUninit<T>, we can just move theTout and leave the memory “uninitialized” without actually having to overwrite its bytes.)
So the buffer will be represented by UnsafeCell<MaybeUninit<T>>.
We’ll also use atomics to represent the head and tail.
struct Queue<T> {
buffer: Vec<UnsafeCell<MaybeUninit<T>>>,
head: AtomicU64,
tail: AtomicU64,
}The producer and consumer types will each have a reference to the queue.
Also, the producer will have a redundant copy of the tail (which slightly reduces contended
access to the shared atomic tail), and likewise,
the consumer will have a redundant copy of the head.
(This is possible because we only have a single producer and consumer each
the producer is the only entity that ever updates the tail and
the consumer is the only entity that ever updates the head.)
pub struct Producer<T> {
queue: Arc<Queue<T>>,
tail: usize,
}
pub struct Consumer<T> {
queue: Arc<Queue<T>>,
head: usize,
}Finally, we come to the actual implementation:
pub fn new_queue<T>(len: usize) -> (Producer<T>, Consumer<T>) {
// Create a vector of UnsafeCells to serve as the ring buffer
let mut backing_cells_vec = Vec::<UnsafeCell<MaybeUninit<T>>>::new();
while backing_cells_vec.len() < len {
let cell = UnsafeCell::new(MaybeUninit::uninit());
backing_cells_vec.push(cell);
}
// Initialize head and tail to 0 (empty)
let head_atomic = AtomicU64::new(0);
let tail_atomic = AtomicU64::new(0);
// Package it all into a queue object, and make a reference-counted pointer to it
// so it can be shared by the Producer and the Consumer.
let queue = Queue::<T> { head: head_atomic, tail: tail_atomic, buffer: backing_cells_vec };
let queue_arc = Arc::new(queue);
let prod = Producer::<T> { queue: queue_arc.clone(), tail: 0 };
let cons = Consumer::<T> { queue: queue_arc, head: 0 };
(prod, cons)
}
impl<T> Producer<T> {
pub fn enqueue(&mut self, t: T) {
// Loop: if the queue is full, then block until it is not.
loop {
let len = self.queue.buffer.len();
// Calculate the index of the slot right after `tail`, wrapping around
// if necessary. If the enqueue is successful, then we will be updating
// the `tail` to this value.
let next_tail = if self.tail + 1 == len { 0 } else { self.tail + 1 };
// Get the current `head` value from the shared atomic.
let head = self.queue.head.load(Ordering::SeqCst);
// Check to make sure there is room. (We can't advance the `tail` pointer
// if it would become equal to the head, since `tail == head` denotes
// an empty state.)
// If there's no room, we'll just loop and try again.
if head != next_tail as u64 {
// Here's the unsafe part: writing the given `t` value into the `UnsafeCell`.
unsafe {
(*self.queue.buffer[self.tail].get()).write(t);
}
// Update the `tail` (both the shared atomic and our local copy).
self.queue.tail.store(next_tail as u64, Ordering::SeqCst);
self.tail = next_tail;
// Done.
return;
}
}
}
}
impl<T> Consumer<T> {
pub fn dequeue(&mut self) -> T {
// Loop: if the queue is empty, then block until it is not.
loop {
let len = self.queue.buffer.len();
// Calculate the index of the slot right after `head`, wrapping around
// if necessary. If the enqueue is successful, then we will be updating
// the `head` to this value.
let next_head = if self.head + 1 == len { 0 } else { self.head + 1 };
// Get the current `tail` value from the shared atomic.
let tail = self.queue.tail.load(Ordering::SeqCst);
// Check to see if the queue is nonempty.
// If it's empty, we'll just loop and try again.
if self.head as u64 != tail {
// Load the stored message from the UnsafeCell
// (replacing it with "uninitialized" memory).
let t = unsafe {
let mut tmp = MaybeUninit::uninit();
std::mem::swap(&mut *self.queue.buffer[self.head].get(), &mut tmp);
tmp.assume_init()
};
// Update the `head` (both the shared atomic and our local copy).
self.queue.head.store(next_head as u64, Ordering::SeqCst);
self.head = next_head;
// Done. Return the value we loaded out of the buffer.
return t;
}
}
}
}Verified implementation
With verification, we always need to start with the question of what, exactly, we are
verifying. In this case, we aren’t actually going to add any new specifications to
the enqueue or dequeue functions; our only aim is to implement the queue and
show that it is memory-type-safe, e.g., that dequeue returns a well-formed T value without
exhibiting any undefined behavior.
Showing this is not actually trivial! The unverified Rust code above used unsafe code,
which means memory-type-safety is not a given.
In our verified queue implementation, we will need a safe, verified alternative to the
unsafe code. We’ll start with introducing our verified alternative to UnsafeCell<MaybeUninit<T>>.
Verified interior mutability with PCell
In Verus, PCell (standing for “permissioned cell”) is the verified equivalent.
(By equivalent, we mean that, subject to inlining and the optimizations doing what we expect,
it ought to generate the same machine code.)
Unlike UnsafeCell, the optional-initializedness is built-in, so PCell<T> can stand in
for UnsafeCell<MaybeUninit<T>>.
In order to verify our use of PCell, Verus requires the user to present a special permission token
on each access (read or write) to the PCell. Each PCell has a unique identifier (given by pcell.id())
and each permission token connects an identifier to the (possibly uninitialized value) stored at the cell.
In the permission token, this value is represented as an Option type, though the option tag has no runtime representation.
fn main() {
// Construct a new pcell and obtain the permission for it.
let (pcell, Tracked(mut perm)) = PCell::<u64>::empty();
// Initially, cell is unitialized, and the `perm` token
// represents that as the value `MemContents::Uninit`.
// The meaning of the permission token is given by its _view_, here `perm@`.
//
// The expression `pcell_opt![ pcell.id() => MemContents::Uninit ]` can be read as roughly,
// "the cell with value pcell.id() is uninitialized".
assert(perm@ === pcell_points![ pcell.id() => MemContents::Uninit ]);
// The above could also be written by accessing the fields of the
// `PointsToData` struct:
assert(perm.id() === pcell.id());
assert(perm.mem_contents() === MemContents::Uninit);
// We can write a value to the pcell (thus initializing it).
// This only requires an `&` reference to the PCell, but it does
// mutate the `perm` token.
pcell.put(Tracked(&mut perm), 5);
// Having written the value, this is reflected in the token:
assert(perm@ === pcell_points![ pcell.id() => MemContents::Init(5) ]);
// We can take the value back out:
let x = pcell.take(Tracked(&mut perm));
// Which leaves it uninitialized again:
assert(x == 5);
assert(perm@ === pcell_points![ pcell.id() => MemContents::Uninit ]);
}After erasure, the above code reduces to something like this:
fn main() {
let pcell = PCell::<u64>::empty();
pcell.put(5);
let x = pcell.take();
}Using PCell in a verified queue.
Let’s look back at the Rust code from above (the code that used UnsafeCell) and mark six points of interest:
four places where we manipulate an atomic and two where we manipulate a cell:
impl<T> Producer<T> {
pub fn enqueue(&mut self, t: T) {
loop {
let len = self.queue.buffer.len();
let next_tail = if self.tail + 1 == len
{ 0 } else { self.tail + 1 };
let head = self.queue.head.load(Ordering::SeqCst); + produce_start (atomic load)
+
if head != next_tail as u64 { +
unsafe { +
(*self.queue.buffer[self.tail].get()).write(t); + write to cell
} +
+
self.queue.tail.store(next_tail as u64, Ordering::SeqCst); + produce_end (atomic store)
self.tail = next_tail;
return;
}
}
}
}
impl<T> Consumer<T> {
pub fn dequeue(&mut self) -> T {
loop {
let len = self.queue.buffer.len();
let next_head = if self.head + 1 == len
{ 0 } else { self.head + 1 };
let tail = self.queue.tail.load(Ordering::SeqCst); + consume_start (atomic load)
+
if self.head as u64 != tail { +
let t = unsafe { +
let mut tmp = MaybeUninit::uninit(); +
std::mem::swap( + read from cell
&mut *self.queue.buffer[self.head].get(), +
&mut tmp); +
tmp.assume_init() +
}; +
+
self.queue.head.store(next_head as u64, Ordering::SeqCst); + consume_end (atomic store)
self.head = next_head;
return t;
}
}
}
}Now, if we’re going to be using a PCell instead of an UnsafeCell, then at the two points where we manipulate the cell,
we are somehow going to need to have the permission token at those points.
Furthermore, we have four points that manipulate atomics. Informally, these atomic operations let us synchronize access to the cell in a data-race-free way. Formally, in the verified setting, these atomics will let us transfer control of the permission tokens that we need to access the cells.
Specifically:
enqueueneeds to obtain the permission atproduce_start, use it to perform a write, and relinquish it atproduce_end.dequeueneeds to obtain the permission atconsume_start, use it to perform a read, and relinquish it atconsume_end.
Woah, woah, woah. Why is this so complicated? We marked the 6 places of interest, so now let’s go build a
tokenized_state_machine!with those 6 transitions already!Good question. That approach might have worked if we were using an atomic to store the value
Tinstead of aPCell(although this would, of course, require theTto be word-sized).However, the
PCellrequires its own considerations. The crucial point is that reading or writing toPCellis non-atomic. That sounds tautological, but I’m not just talking about the name of the type here. By atomic or non-atomic, I’m actually referring to the atomicity of the operation in the execution model. We can’t freely abstractPCelloperations as atomic operations that allow arbitrary interleaving.Okay, so what would go wrong in Verus if we tried?
Recall how it works for atomic memory locations. With an atomic memory location, we can access it any time if we just have an atomic invariant for it. We open the invariant (acquiring permission to access the value along with any ghost data), perform the operation, which is atomic, and then close the invariant. In this scenario, the invariant is restored after a single atomic operation, as is necessary.
But we can’t do the same for
PCell.PCelloperations are non-atomic, so we can’t perform aPCellread or write while an atomic invariant is open. Thus, thePCell’s permission token needs to be transferred at the points in the program where we are performing atomic operations, that is, at the four marked atomic operations.
Abstracting the program while handling permissions
Verus’s tokenized_state_machine! supports a notion called storage.
An instance of a protocol is allowed to store tokens, which client threads can operate on
by temporarily “checking them out”. This provides a convenient means for transferring ownership of
tokens through the system.
Think of the instance as like a library. (Actually, think of it like a network of libraries with an inter-library loan system, where the librarians tirelessly follow a protocol to make sure any given library has a book whenever a patron is ready to check a book out.)
Anyway, the tokenized_state_machine! we’ll use here should look something like this:
- It should be able to store all the permission tokens for each
PCellin the buffer. - It should have 4 transitions:
produce_startshould allow the producer to “check out” the permission for the cell that it is ready to write to.produce_endshould allow the producer to “check back in” the permission that it checked out.consume_startshould allow the consumer to “check out” the permission for the cell that it is ready to read from.consume_endshould allow the consumer to “check back in” the permission that it checked out.
Hang on, I read ahead and learned that Verus’s storage mechanism has a different mechanism for handling reads. Why aren’t we using that for the consumer?
A few reasons.
- That mechanism is useful specifically for read-sharing, which we aren’t using here.
- We actually can’t use it, since the “read” isn’t really a read. Well, at the byte-level, it should just be a read. But we actually do change the value that is stored there in the high-level program semantics: we move the value out and replaced it with an “uninitialized” value. And we have to do it this way, unless
TimplementedCopy.
The producer and consumer each have a small “view into the world”: each one might have access to one of the permission tokens if they have it “checked out”, but that’s it.
To understand the state machine protocol we’re going to build, we have to look at the protocol dually to the producer and the consumer. If the producer and consumer might have 0 or 1 permissions checked out at a given time, then complementarily, the protocol state should be “almost all of the permissions, except possibly up to 2 permissions that are currently checked out”.
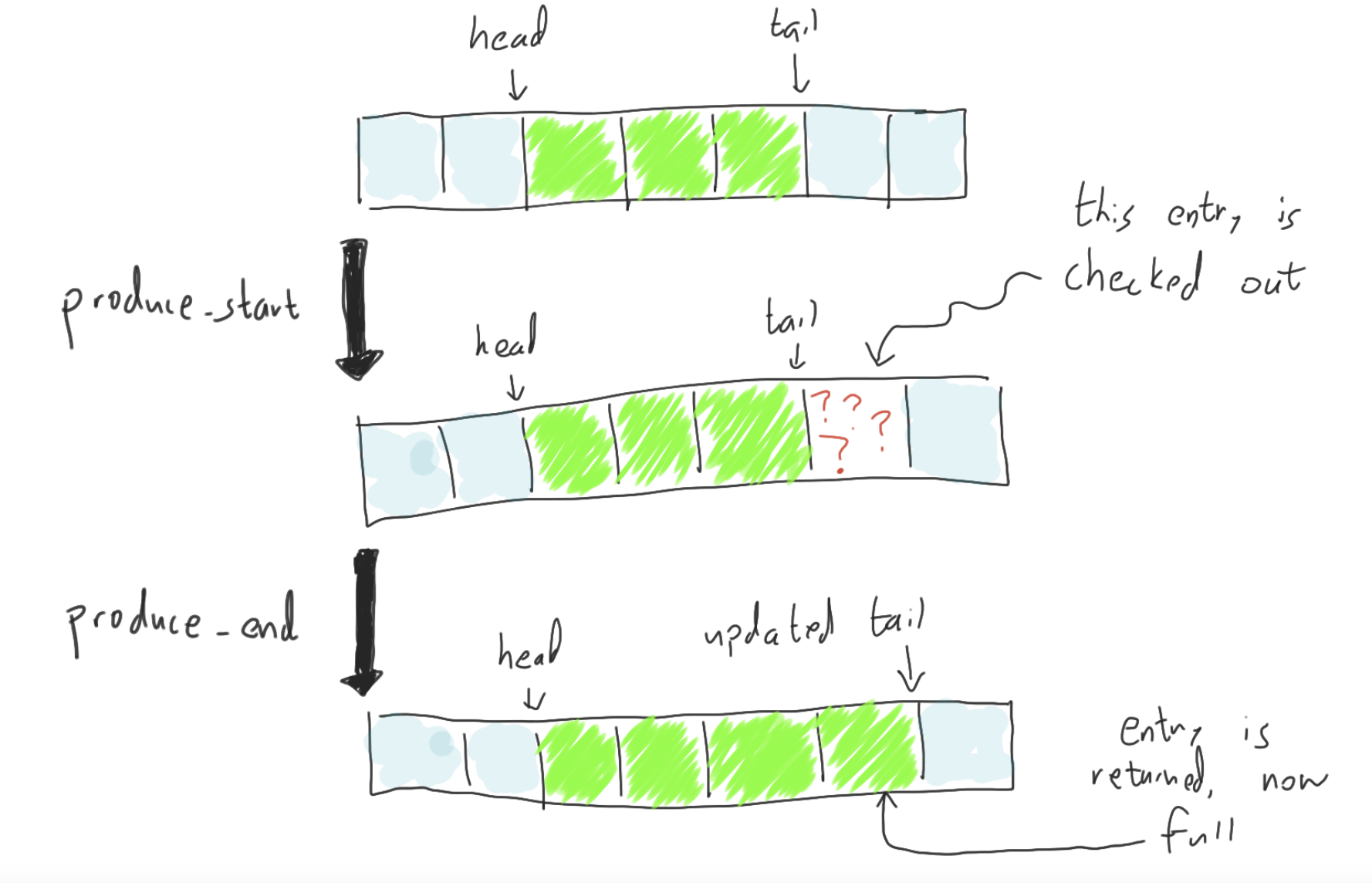
For example, here is the full sequence of operations for an enqueue step, both from the perspective of the producer
and of the storage protocol:
| operation | Producer’s perspective | Storage protocol’s perspective |
|---|---|---|
produce_start | receives a permission for an uninitialized cell | lends out a permission for an uninitialized cell |
| write to the cell | writes to the cell with PCell::put | |
produce_end | returns a permission for the now-initialized cell | receives back the permission, now initialized |
And here is the storage protocol’s perspective, graphically:
Building the tokenized_state_machine!
Now that we finally have a handle on the protocol, let’s implement it. It should have all the following state:
- The value of the shared
headatomic - The value of the shared
tailatomic - The producer’s state
- Is the producer step in progress?
- Local
tailfield saved by the producer
- The consumer’s state
- Is the consumer step in progress?
- Local
headfield saved by the producer
- The IDs of cells in the buffer (so we know what permissions we’re meant to be storing)
- The permissions that are actually stored.
And now, in code:
#[is_variant]
pub enum ProducerState {
Idle(nat), // local copy of tail
Producing(nat),
}
#[is_variant]
pub enum ConsumerState {
Idle(nat), // local copy of head
Consuming(nat),
}
tokenized_state_machine!{FifoQueue<T> {
fields {
// IDs of the cells used in the ring buffer.
// These are fixed throughout the protocol.
#[sharding(constant)]
pub backing_cells: Seq<CellId>,
// All the stored permissions
#[sharding(storage_map)]
pub storage: Map<nat, cell::PointsTo<T>>,
// Represents the shared `head` field
#[sharding(variable)]
pub head: nat,
// Represents the shared `tail` field
#[sharding(variable)]
pub tail: nat,
// Represents the local state of the single-producer
#[sharding(variable)]
pub producer: ProducerState,
// Represents the local state of the single-consumer
#[sharding(variable)]
pub consumer: ConsumerState,
}
// ...
}}As you can see, Verus allows us to utilize storage by declaring it in the sharding strategy.
Here, the strategy we use is storage_map. In the storage_map strategy,
the stored token items are given by the values in the map.
The keys in the map can be an arbitrary type that we choose to use as an index to refer to
stored items. Here, the index we’ll use will just the index into the queue.
Thus keys of the storage map will take on values in the range [0, len).
Hmm. For a second, I thought you were going to use the cell IDs as keys in the map. Could it work that way as well?
Yes, although it would be slightly more complicated. For one, we’d need to track an invariant that all the IDs are distinct, just to show that there aren’t overlapping keys. But that’s an extra invariant to prove that we don’t need if we do it this way. Much easier to declare a correspondance between
backing_cells[i]andstorage[i]for eachi.Wait, does that mean we aren’t going to prove an invariant that all the IDs are distinct? That can’t possibly be right, right?
It does mean that!
Certainly, it is true that in any execution of the program, the IDs of the cells are going to be distinct, but this isn’t something we need to track ourselves as users of the
PCelllibrary.You might be familiar with an approach where we have some kind of “heap model,” which maps addresses to values. When we update one entry, we have to show how nothing else of interest is changing. But like I just said, we aren’t using that sort of heap model in the
Fifoprotocol, we’re just indexing based on queue index. And we don’t rely on any sort of heap model like that in the implementations ofenqueueordequeueeither; there, we use the separated permission model.
Now, let’s dive into the transitions. Let’s start with produce_start transition.
transition!{
produce_start() {
// In order to begin, we have to be in ProducerState::Idle.
require(pre.producer.is_Idle());
// We'll be comparing the producer's _local_ copy of the tail
// with the _shared_ version of the head.
let tail = pre.producer.get_Idle_0();
let head = pre.head;
assert(0 <= tail && tail < pre.backing_cells.len());
// Compute the incremented tail, wrapping around if necessary.
let next_tail = Self::inc_wrap(tail, pre.backing_cells.len());
// We have to check that the buffer isn't full to proceed.
require(next_tail != head);
// Update the producer's local state to be in the `Producing` state.
update producer = ProducerState::Producing(tail);
// Withdraw ("check out") the permission stored at index `tail`.
// This creates a proof obligation for the transition system to prove that
// there is actually a permission stored at this index.
withdraw storage -= [tail => let perm] by {
assert(pre.valid_storage_at_idx(tail));
};
// The transition needs to guarantee to the client that the
// permission they are checking out:
// (i) is for the cell at index `tail` (the IDs match)
// (ii) the permission indicates that the cell is empty
assert(
perm.id() === pre.backing_cells.index(tail as int)
&& perm.is_uninit()
) by {
assert(!pre.in_active_range(tail));
assert(pre.valid_storage_at_idx(tail));
};
}
}It’s a doozy, but we just need to break it down into three parts:
- The enabling conditions (
require).- The client needs to exhibit that these conditions hold
(e.g., by doing the approparite comparison between the
headandtailvalues) in order to perform the transition.
- The client needs to exhibit that these conditions hold
(e.g., by doing the approparite comparison between the
- The stuff that gets updated:
- We
updatethe producer’s local state - We
withdraw(“check out”) the permission, which is represented simply by removing the key from the map.
- We
- Guarantees about the result of the transition.
- These guarantees will follow from internal invariants about the
FifoQueuesystem - In this case, we care about guarantees on the permission token that is checked out.
- These guarantees will follow from internal invariants about the
Now, let’s see produce_end. The main difference, here, is that the client is checking the permission token
back into the system, which means we have to provide the guarantees about the permission token
in the enabing condition rather than in a post-guarantee.
transition!{
// This transition is parameterized by the value of the permission
// being inserted. Since the permission is being deposited
// (coming from "outside" the system) we can't compute it as a
// function of the current state, unlike how we did it for the
// `produce_start` transition).
produce_end(perm: cell::PointsTo<T>) {
// In order to complete the produce step,
// we have to be in ProducerState::Producing.
require(pre.producer.is_Producing());
let tail = pre.producer.get_Producing_0();
assert(0 <= tail && tail < pre.backing_cells.len());
// Compute the incremented tail, wrapping around if necessary.
let next_tail = Self::inc_wrap(tail, pre.backing_cells.len());
// This time, we don't need to compare the `head` and `tail` - we already
// check that, and anyway, we don't have access to the `head` field
// for this transition. (This transition is supposed to occur while
// modifying the `tail` field, so we can't do both.)
// However, we _do_ need to check that the permission token being
// checked in satisfies its requirements. It has to be associated
// with the correct cell, and it has to be full.
require(perm.id() === pre.backing_cells.index(tail as int)
&& perm.is_init());
// Perform our updates. Update the tail to the computed value,
// both the shared version and the producer's local copy.
// Also, move back to the Idle state.
update producer = ProducerState::Idle(next_tail);
update tail = next_tail;
// Check the permission back into the storage map.
deposit storage += [tail => perm] by { assert(pre.valid_storage_at_idx(tail)); };
}
}Check the full source for the consume_start and consume_end transitions, which are pretty similar,
and for the invariants we use to prove that the transitions are all well-formed.
Verified Implementation
For the implementation, let’s start with the definitions for the Producer, Consumer, and Queue structs,
which are based on the ones from the unverified implementation, augmented with proof variables.
The Producer, for example, gets a proof token for the producer: ProducerState field.
The well-formedness condition here demands us to be in the ProducerState::Idle state
(in every call to enqueue, we must start and end in the Idle state).
pub struct Producer<T> {
queue: Arc<Queue<T>>,
tail: usize,
producer: Tracked<FifoQueue::producer<T>>,
}
impl<T> Producer<T> {
pub closed spec fn wf(&self) -> bool {
(*self.queue).wf()
&& self.producer@.instance_id() == (*self.queue).instance@.id()
&& self.producer@.value() == ProducerState::Idle(self.tail as nat)
&& (self.tail as int) < (*self.queue).buffer@.len()
}
}For the Queue type itself, we add an atomic invariant for the head and tail fields:
struct_with_invariants!{
struct Queue<T> {
buffer: Vec<PCell<T>>,
head: AtomicU64<_, FifoQueue::head<T>, _>,
tail: AtomicU64<_, FifoQueue::tail<T>, _>,
instance: Tracked<FifoQueue::Instance<T>>,
}
pub closed spec fn wf(&self) -> bool {
predicate {
// The Cell IDs in the instance protocol match the cell IDs in the actual vector:
&&& self.instance@.backing_cells().len() == self.buffer@.len()
&&& forall|i: int| 0 <= i && i < self.buffer@.len() as int ==>
self.instance@.backing_cells().index(i) ===
self.buffer@.index(i).id()
}
invariant on head with (instance) is (v: u64, g: FifoQueue::head<T>) {
&&& g.instance_id() === instance@.id()
&&& g.value() == v as int
}
invariant on tail with (instance) is (v: u64, g: FifoQueue::tail<T>) {
&&& g.instance_id() === instance@.id()
&&& g.value() == v as int
}
}
}Now we can implement and verify enqueue:
impl<T> Producer<T> {
fn enqueue(&mut self, t: T)
requires
old(self).wf(),
ensures
self.wf(),
{
// Loop: if the queue is full, then block until it is not.
loop
invariant
self.wf(),
{
let queue = &*self.queue;
let len = queue.buffer.len();
assert(0 <= self.tail && self.tail < len);
// Calculate the index of the slot right after `tail`, wrapping around
// if necessary. If the enqueue is successful, then we will be updating
// the `tail` to this value.
let next_tail = if self.tail + 1 == len {
0
} else {
self.tail + 1
};
let tracked cell_perm: Option<cell::PointsTo<T>>;
// Get the current `head` value from the shared atomic.
let head =
atomic_with_ghost!(&queue.head => load();
returning head;
ghost head_token => {
// If `head != next_tail`, then we proceed with the operation.
// We check here, ghostily, in the `open_atomic_invariant` block if that's the case.
// If so, we proceed with the `produce_start` transition
// and obtain the cell permission.
cell_perm = if head != next_tail as u64 {
let tracked cp = queue.instance.borrow().produce_start(&head_token, self.producer.borrow_mut());
Option::Some(cp)
} else {
Option::None
};
}
);
// Here's where we "actually" do the `head != next_tail` check:
if head != next_tail as u64 {
// Unwrap the cell_perm from the option.
let tracked mut cell_perm = match cell_perm {
Option::Some(cp) => cp,
Option::None => {
assert(false);
proof_from_false()
},
};
// Write the element t into the buffer, updating the cell
// from uninitialized to initialized (to the value t).
queue.buffer[self.tail].put(Tracked(&mut cell_perm), t);
// Store the updated tail to the shared `tail` atomic,
// while performing the `produce_end` transition.
atomic_with_ghost!(&queue.tail => store(next_tail as u64); ghost tail_token => {
queue.instance.borrow().produce_end(cell_perm,
cell_perm, &mut tail_token, self.producer.borrow_mut());
});
self.tail = next_tail;
return ;
}
}
}
}Single-Producer, Single-Consumer queue, unverified Rust source
// Ordinary Rust code, not Verus
use std::cell::UnsafeCell;
use std::mem::MaybeUninit;
use std::sync::atomic::{AtomicU64, Ordering};
use std::sync::Arc;
struct Queue<T> {
buffer: Vec<UnsafeCell<MaybeUninit<T>>>,
head: AtomicU64,
tail: AtomicU64,
}
pub struct Producer<T> {
queue: Arc<Queue<T>>,
tail: usize,
}
pub struct Consumer<T> {
queue: Arc<Queue<T>>,
head: usize,
}
pub fn new_queue<T>(len: usize) -> (Producer<T>, Consumer<T>) {
// Create a vector of UnsafeCells to serve as the ring buffer
let mut backing_cells_vec = Vec::<UnsafeCell<MaybeUninit<T>>>::new();
while backing_cells_vec.len() < len {
let cell = UnsafeCell::new(MaybeUninit::uninit());
backing_cells_vec.push(cell);
}
// Initialize head and tail to 0 (empty)
let head_atomic = AtomicU64::new(0);
let tail_atomic = AtomicU64::new(0);
// Package it all into a queue object, and make a reference-counted pointer to it
// so it can be shared by the Producer and the Consumer.
let queue = Queue::<T> { head: head_atomic, tail: tail_atomic, buffer: backing_cells_vec };
let queue_arc = Arc::new(queue);
let prod = Producer::<T> { queue: queue_arc.clone(), tail: 0 };
let cons = Consumer::<T> { queue: queue_arc, head: 0 };
(prod, cons)
}
impl<T> Producer<T> {
pub fn enqueue(&mut self, t: T) {
// Loop: if the queue is full, then block until it is not.
loop {
let len = self.queue.buffer.len();
// Calculate the index of the slot right after `tail`, wrapping around
// if necessary. If the enqueue is successful, then we will be updating
// the `tail` to this value.
let next_tail = if self.tail + 1 == len { 0 } else { self.tail + 1 };
// Get the current `head` value from the shared atomic.
let head = self.queue.head.load(Ordering::SeqCst);
// Check to make sure there is room. (We can't advance the `tail` pointer
// if it would become equal to the head, since `tail == head` denotes
// an empty state.)
// If there's no room, we'll just loop and try again.
if head != next_tail as u64 {
// Here's the unsafe part: writing the given `t` value into the `UnsafeCell`.
unsafe {
(*self.queue.buffer[self.tail].get()).write(t);
}
// Update the `tail` (both the shared atomic and our local copy).
self.queue.tail.store(next_tail as u64, Ordering::SeqCst);
self.tail = next_tail;
// Done.
return;
}
}
}
}
impl<T> Consumer<T> {
pub fn dequeue(&mut self) -> T {
// Loop: if the queue is empty, then block until it is not.
loop {
let len = self.queue.buffer.len();
// Calculate the index of the slot right after `head`, wrapping around
// if necessary. If the enqueue is successful, then we will be updating
// the `head` to this value.
let next_head = if self.head + 1 == len { 0 } else { self.head + 1 };
// Get the current `tail` value from the shared atomic.
let tail = self.queue.tail.load(Ordering::SeqCst);
// Check to see if the queue is nonempty.
// If it's empty, we'll just loop and try again.
if self.head as u64 != tail {
// Load the stored message from the UnsafeCell
// (replacing it with "uninitialized" memory).
let t = unsafe {
let mut tmp = MaybeUninit::uninit();
std::mem::swap(&mut *self.queue.buffer[self.head].get(), &mut tmp);
tmp.assume_init()
};
// Update the `head` (both the shared atomic and our local copy).
self.queue.head.store(next_head as u64, Ordering::SeqCst);
self.head = next_head;
// Done. Return the value we loaded out of the buffer.
return t;
}
}
}
}
fn main() {
let (mut producer, mut consumer) = new_queue(20);
producer.enqueue(5);
let _x = consumer.dequeue();
}Single-Producer, Single-Consumer queue, example source
use std::sync::Arc;
use vstd::atomic_ghost::*;
use vstd::cell::*;
use vstd::map::*;
use vstd::modes::*;
use vstd::multiset::*;
use vstd::prelude::*;
use vstd::seq::*;
use vstd::{pervasive::*, prelude::*, *};
verus! {
use verus_state_machines_macros::tokenized_state_machine;
#[is_variant]
pub enum ProducerState {
Idle(nat), // local copy of tail
Producing(nat),
}
#[is_variant]
pub enum ConsumerState {
Idle(nat), // local copy of head
Consuming(nat),
}
tokenized_state_machine!{FifoQueue<T> {
fields {
// IDs of the cells used in the ring buffer.
// These are fixed throughout the protocol.
#[sharding(constant)]
pub backing_cells: Seq<CellId>,
// All the stored permissions
#[sharding(storage_map)]
pub storage: Map<nat, cell::PointsTo<T>>,
// Represents the shared `head` field
#[sharding(variable)]
pub head: nat,
// Represents the shared `tail` field
#[sharding(variable)]
pub tail: nat,
// Represents the local state of the single-producer
#[sharding(variable)]
pub producer: ProducerState,
// Represents the local state of the single-consumer
#[sharding(variable)]
pub consumer: ConsumerState,
}
pub open spec fn len(&self) -> nat {
self.backing_cells.len()
}
pub open spec fn inc_wrap(i: nat, len: nat) -> nat {
if i + 1 == len { 0 } else { i + 1 }
}
// Make sure the producer state and the consumer state aren't inconsistent.
#[invariant]
pub fn not_overlapping(&self) -> bool {
match (self.producer, self.consumer) {
(ProducerState::Producing(tail), ConsumerState::Idle(head)) => {
Self::inc_wrap(tail, self.len()) != head
}
(ProducerState::Producing(tail), ConsumerState::Consuming(head)) => {
head != tail
&& Self::inc_wrap(tail, self.len()) != head
}
(ProducerState::Idle(tail), ConsumerState::Idle(head)) => {
true
}
(ProducerState::Idle(tail), ConsumerState::Consuming(head)) => {
head != tail
}
}
}
// `head` and `tail` are in-bounds
// shared `head` and `tail` fields agree with the ProducerState and ConsumerState
#[invariant]
pub fn in_bounds(&self) -> bool {
0 <= self.head && self.head < self.len() &&
0 <= self.tail && self.tail < self.len()
&& match self.producer {
ProducerState::Producing(tail) => {
self.tail == tail
}
ProducerState::Idle(tail) => {
self.tail == tail
}
}
&& match self.consumer {
ConsumerState::Consuming(head) => {
self.head == head
}
ConsumerState::Idle(head) => {
self.head == head
}
}
}
// Indicates whether we expect the cell at index `i` to be full based on
// the values of the `head` and `tail`.
pub open spec fn in_active_range(&self, i: nat) -> bool {
// Note that self.head = self.tail means empty range
0 <= i && i < self.len() && (
if self.head <= self.tail {
self.head <= i && i < self.tail
} else {
i >= self.head || i < self.tail
}
)
}
// Indicates whether we expect a cell to be checked out or not,
// based on the producer/consumer state.
pub open spec fn is_checked_out(&self, i: nat) -> bool {
self.producer === ProducerState::Producing(i)
|| self.consumer === ConsumerState::Consuming(i)
}
// Predicate to determine that the state at cell index `i`
// is correct. For each index, there are three possibilities:
//
// 1. No cell permission is stored
// 2. Permission is stored; permission indicates a full cell
// 3. Permission is stored; permission indicates an empty cell
//
// Which of these 3 possibilities we should be in depends on the
// producer/consumer/head/tail state.
pub open spec fn valid_storage_at_idx(&self, i: nat) -> bool {
if self.is_checked_out(i) {
// No cell permission is stored
!self.storage.dom().contains(i)
} else {
// Permission is stored
self.storage.dom().contains(i)
// Permission must be for the correct cell:
&& self.storage.index(i).id() === self.backing_cells.index(i as int)
&& if self.in_active_range(i) {
// The cell is full
self.storage.index(i).is_init()
} else {
// The cell is empty
self.storage.index(i).is_uninit()
}
}
}
#[invariant]
pub fn valid_storage_all(&self) -> bool {
forall|i: nat| 0 <= i && i < self.len() ==>
self.valid_storage_at_idx(i)
}
init!{
initialize(backing_cells: Seq<CellId>, storage: Map<nat, cell::PointsTo<T>>) {
// Upon initialization, the user needs to deposit _all_ the relevant
// cell permissions to start with. Each permission should indicate
// an empty cell.
require(
(forall|i: nat| 0 <= i && i < backing_cells.len() ==>
#[trigger] storage.dom().contains(i)
&& storage.index(i).id() === backing_cells.index(i as int)
&& storage.index(i).is_uninit())
);
require(backing_cells.len() > 0);
init backing_cells = backing_cells;
init storage = storage;
init head = 0;
init tail = 0;
init producer = ProducerState::Idle(0);
init consumer = ConsumerState::Idle(0);
}
}
transition!{
produce_start() {
// In order to begin, we have to be in ProducerState::Idle.
require(pre.producer.is_Idle());
// We'll be comparing the producer's _local_ copy of the tail
// with the _shared_ version of the head.
let tail = pre.producer.get_Idle_0();
let head = pre.head;
assert(0 <= tail && tail < pre.backing_cells.len());
// Compute the incremented tail, wrapping around if necessary.
let next_tail = Self::inc_wrap(tail, pre.backing_cells.len());
// We have to check that the buffer isn't full to proceed.
require(next_tail != head);
// Update the producer's local state to be in the `Producing` state.
update producer = ProducerState::Producing(tail);
// Withdraw ("check out") the permission stored at index `tail`.
// This creates a proof obligation for the transition system to prove that
// there is actually a permission stored at this index.
withdraw storage -= [tail => let perm] by {
assert(pre.valid_storage_at_idx(tail));
};
// The transition needs to guarantee to the client that the
// permission they are checking out:
// (i) is for the cell at index `tail` (the IDs match)
// (ii) the permission indicates that the cell is empty
assert(
perm.id() === pre.backing_cells.index(tail as int)
&& perm.is_uninit()
) by {
assert(!pre.in_active_range(tail));
assert(pre.valid_storage_at_idx(tail));
};
}
}
transition!{
// This transition is parameterized by the value of the permission
// being inserted. Since the permission is being deposited
// (coming from "outside" the system) we can't compute it as a
// function of the current state, unlike how we did it for the
// `produce_start` transition).
produce_end(perm: cell::PointsTo<T>) {
// In order to complete the produce step,
// we have to be in ProducerState::Producing.
require(pre.producer.is_Producing());
let tail = pre.producer.get_Producing_0();
assert(0 <= tail && tail < pre.backing_cells.len());
// Compute the incremented tail, wrapping around if necessary.
let next_tail = Self::inc_wrap(tail, pre.backing_cells.len());
// This time, we don't need to compare the `head` and `tail` - we already
// check that, and anyway, we don't have access to the `head` field
// for this transition. (This transition is supposed to occur while
// modifying the `tail` field, so we can't do both.)
// However, we _do_ need to check that the permission token being
// checked in satisfies its requirements. It has to be associated
// with the correct cell, and it has to be full.
require(perm.id() === pre.backing_cells.index(tail as int)
&& perm.is_init());
// Perform our updates. Update the tail to the computed value,
// both the shared version and the producer's local copy.
// Also, move back to the Idle state.
update producer = ProducerState::Idle(next_tail);
update tail = next_tail;
// Check the permission back into the storage map.
deposit storage += [tail => perm] by { assert(pre.valid_storage_at_idx(tail)); };
}
}
transition!{
consume_start() {
// In order to begin, we have to be in ConsumerState::Idle.
require(pre.consumer.is_Idle());
// We'll be comparing the consumer's _local_ copy of the head
// with the _shared_ version of the tail.
let head = pre.consumer.get_Idle_0();
let tail = pre.tail;
assert(0 <= head && head < pre.backing_cells.len());
// We have to check that the buffer isn't empty to proceed.
require(head != tail);
// Update the consumer's local state to be in the `Consuming` state.
update consumer = ConsumerState::Consuming(head);
// Withdraw ("check out") the permission stored at index `tail`.
birds_eye let perm = pre.storage.index(head);
withdraw storage -= [head => perm] by {
assert(pre.valid_storage_at_idx(head));
};
assert(perm.id() === pre.backing_cells.index(head as int)) by {
assert(pre.valid_storage_at_idx(head));
};
assert(perm.is_init()) by {
assert(pre.in_active_range(head));
assert(pre.valid_storage_at_idx(head));
};
}
}
transition!{
consume_end(perm: cell::PointsTo<T>) {
require(pre.consumer.is_Consuming());
let head = pre.consumer.get_Consuming_0();
assert(0 <= head && head < pre.backing_cells.len());
let next_head = Self::inc_wrap(head, pre.backing_cells.len());
update consumer = ConsumerState::Idle(next_head);
update head = next_head;
require(perm.id() === pre.backing_cells.index(head as int)
&& perm.is_uninit());
deposit storage += [head => perm] by { assert(pre.valid_storage_at_idx(head)); };
}
}
#[inductive(initialize)]
fn initialize_inductive(post: Self, backing_cells: Seq<CellId>, storage: Map<nat, cell::PointsTo<T>>) {
assert forall|i: nat|
0 <= i && i < post.len() implies post.valid_storage_at_idx(i)
by {
assert(post.storage.dom().contains(i));
/*
assert(
post.storage.index(i).id() ===
post.backing_cells.index(i)
);
assert(if post.in_active_range(i) {
post.storage.index(i).value.is_Some()
} else {
post.storage.index(i).value.is_None()
});*/
}
}
//// Invariant proofs
#[inductive(produce_start)]
fn produce_start_inductive(pre: Self, post: Self) {
let tail = pre.producer.get_Idle_0();
assert(!pre.in_active_range(tail));
match (post.producer, post.consumer) {
(ProducerState::Producing(tail), ConsumerState::Idle(head)) => {
assert(Self::inc_wrap(tail, post.len()) != head);
}
(ProducerState::Producing(tail), ConsumerState::Consuming(head)) => {
assert(head != tail);
assert(Self::inc_wrap(tail, post.len()) != head);
}
(ProducerState::Idle(tail), ConsumerState::Idle(head)) => {
}
(ProducerState::Idle(tail), ConsumerState::Consuming(head)) => {
assert(head != tail);
}
}
assert(forall|i| pre.valid_storage_at_idx(i) ==> post.valid_storage_at_idx(i));
}
#[inductive(produce_end)]
fn produce_end_inductive(pre: Self, post: Self, perm: cell::PointsTo<T>) {
assert forall |i|
pre.valid_storage_at_idx(i) implies
post.valid_storage_at_idx(i)
by {
/*if post.is_checked_out(i) {
assert(!post.storage.dom().contains(i));
} else {
assert(post.storage.dom().contains(i));
assert(
post.storage.index(i).id() ===
post.backing_cells.index(i)
);
assert(if post.in_active_range(i) {
post.storage.index(i).value.is_Some()
} else {
post.storage.index(i).value.is_None()
});
}*/
}
}
#[inductive(consume_start)]
fn consume_start_inductive(pre: Self, post: Self) {
assert forall |i|
pre.valid_storage_at_idx(i) implies post.valid_storage_at_idx(i)
by { }
}
#[inductive(consume_end)]
fn consume_end_inductive(pre: Self, post: Self, perm: cell::PointsTo<T>) {
let head = pre.consumer.get_Consuming_0();
assert(post.storage.dom().contains(head));
assert(
post.storage.index(head).id() ===
post.backing_cells.index(head as int)
);
assert(if post.in_active_range(head) {
post.storage.index(head).is_init()
} else {
post.storage.index(head).is_uninit()
});
match (pre.producer, pre.consumer) {
(ProducerState::Producing(tail), ConsumerState::Idle(head)) => {
assert(pre.head != pre.tail);
}
(ProducerState::Producing(tail), ConsumerState::Consuming(head)) => {
assert(pre.head != pre.tail);
}
(ProducerState::Idle(tail), ConsumerState::Idle(head)) => {
assert(pre.head != pre.tail);
}
(ProducerState::Idle(tail), ConsumerState::Consuming(head)) => {
assert(pre.head != pre.tail);
}
};
assert(pre.head != pre.tail);
assert(!post.is_checked_out(head));
assert(post.valid_storage_at_idx(head));
assert forall |i|
pre.valid_storage_at_idx(i) implies post.valid_storage_at_idx(i)
by { }
}
}}
struct_with_invariants!{
struct Queue<T> {
buffer: Vec<PCell<T>>,
head: AtomicU64<_, FifoQueue::head<T>, _>,
tail: AtomicU64<_, FifoQueue::tail<T>, _>,
instance: Tracked<FifoQueue::Instance<T>>,
}
pub closed spec fn wf(&self) -> bool {
predicate {
// The Cell IDs in the instance protocol match the cell IDs in the actual vector:
&&& self.instance@.backing_cells().len() == self.buffer@.len()
&&& forall|i: int| 0 <= i && i < self.buffer@.len() as int ==>
self.instance@.backing_cells().index(i) ===
self.buffer@.index(i).id()
}
invariant on head with (instance) is (v: u64, g: FifoQueue::head<T>) {
&&& g.instance_id() === instance@.id()
&&& g.value() == v as int
}
invariant on tail with (instance) is (v: u64, g: FifoQueue::tail<T>) {
&&& g.instance_id() === instance@.id()
&&& g.value() == v as int
}
}
}
pub struct Producer<T> {
queue: Arc<Queue<T>>,
tail: usize,
producer: Tracked<FifoQueue::producer<T>>,
}
impl<T> Producer<T> {
pub closed spec fn wf(&self) -> bool {
(*self.queue).wf()
&& self.producer@.instance_id() == (*self.queue).instance@.id()
&& self.producer@.value() == ProducerState::Idle(self.tail as nat)
&& (self.tail as int) < (*self.queue).buffer@.len()
}
}
pub struct Consumer<T> {
queue: Arc<Queue<T>>,
head: usize,
consumer: Tracked<FifoQueue::consumer<T>>,
}
impl<T> Consumer<T> {
pub closed spec fn wf(&self) -> bool {
(*self.queue).wf()
&& self.consumer@.instance_id() === (*self.queue).instance@.id()
&& self.consumer@.value() === ConsumerState::Idle(self.head as nat)
&& (self.head as int) < (*self.queue).buffer@.len()
}
}
pub fn new_queue<T>(len: usize) -> (pc: (Producer<T>, Consumer<T>))
requires
len > 0,
ensures
pc.0.wf(),
pc.1.wf(),
{
// Initialize the vector to store the cells
let mut backing_cells_vec = Vec::<PCell<T>>::new();
// Initialize map for the permissions to the cells
// (keyed by the indices into the vector)
let tracked mut perms = Map::<nat, cell::PointsTo<T>>::tracked_empty();
while backing_cells_vec.len() < len
invariant
forall|j: nat|
#![trigger( perms.dom().contains(j) )]
#![trigger( backing_cells_vec@.index(j as int) )]
#![trigger( perms.index(j) )]
0 <= j && j < backing_cells_vec.len() as int ==> perms.dom().contains(j)
&& backing_cells_vec@.index(j as int).id() === perms.index(j).id()
&& perms.index(j).is_uninit(),
{
let ghost i = backing_cells_vec.len();
let (cell, cell_perm) = PCell::empty();
backing_cells_vec.push(cell);
proof {
perms.tracked_insert(i as nat, cell_perm.get());
}
assert(perms.dom().contains(i as nat));
assert(backing_cells_vec@.index(i as int).id() === perms.index(i as nat).id());
assert(perms.index(i as nat).is_uninit());
}
// Vector for ids
let ghost mut backing_cells_ids = Seq::<CellId>::new(
backing_cells_vec@.len(),
|i: int| backing_cells_vec@.index(i).id(),
);
// Initialize an instance of the FIFO queue
let tracked (
Tracked(instance),
Tracked(head_token),
Tracked(tail_token),
Tracked(producer_token),
Tracked(consumer_token),
) = FifoQueue::Instance::initialize(backing_cells_ids, perms, perms);
// Initialize atomics
let tracked_inst: Tracked<FifoQueue::Instance<T>> = Tracked(instance.clone());
let head_atomic = AtomicU64::new(Ghost(tracked_inst), 0, Tracked(head_token));
let tail_atomic = AtomicU64::new(Ghost(tracked_inst), 0, Tracked(tail_token));
// Initialize the queue
let queue = Queue::<T> {
instance: Tracked(instance),
head: head_atomic,
tail: tail_atomic,
buffer: backing_cells_vec,
};
// Share the queue between the producer and consumer
let queue_arc = Arc::new(queue);
let prod = Producer::<T> {
queue: queue_arc.clone(),
tail: 0,
producer: Tracked(producer_token),
};
let cons = Consumer::<T> { queue: queue_arc, head: 0, consumer: Tracked(consumer_token) };
(prod, cons)
}
impl<T> Producer<T> {
fn enqueue(&mut self, t: T)
requires
old(self).wf(),
ensures
self.wf(),
{
// Loop: if the queue is full, then block until it is not.
loop
invariant
self.wf(),
{
let queue = &*self.queue;
let len = queue.buffer.len();
assert(0 <= self.tail && self.tail < len);
// Calculate the index of the slot right after `tail`, wrapping around
// if necessary. If the enqueue is successful, then we will be updating
// the `tail` to this value.
let next_tail = if self.tail + 1 == len {
0
} else {
self.tail + 1
};
let tracked cell_perm: Option<cell::PointsTo<T>>;
// Get the current `head` value from the shared atomic.
let head =
atomic_with_ghost!(&queue.head => load();
returning head;
ghost head_token => {
// If `head != next_tail`, then we proceed with the operation.
// We check here, ghostily, in the `open_atomic_invariant` block if that's the case.
// If so, we proceed with the `produce_start` transition
// and obtain the cell permission.
cell_perm = if head != next_tail as u64 {
let tracked cp = queue.instance.borrow().produce_start(&head_token, self.producer.borrow_mut());
Option::Some(cp)
} else {
Option::None
};
}
);
// Here's where we "actually" do the `head != next_tail` check:
if head != next_tail as u64 {
// Unwrap the cell_perm from the option.
let tracked mut cell_perm = match cell_perm {
Option::Some(cp) => cp,
Option::None => {
assert(false);
proof_from_false()
},
};
// Write the element t into the buffer, updating the cell
// from uninitialized to initialized (to the value t).
queue.buffer[self.tail].put(Tracked(&mut cell_perm), t);
// Store the updated tail to the shared `tail` atomic,
// while performing the `produce_end` transition.
atomic_with_ghost!(&queue.tail => store(next_tail as u64); ghost tail_token => {
queue.instance.borrow().produce_end(cell_perm,
cell_perm, &mut tail_token, self.producer.borrow_mut());
});
self.tail = next_tail;
return ;
}
}
}
}
impl<T> Consumer<T> {
fn dequeue(&mut self) -> (t: T)
requires
old(self).wf(),
ensures
self.wf(),
{
loop
invariant
self.wf(),
{
let queue = &*self.queue;
let len = queue.buffer.len();
assert(0 <= self.head && self.head < len);
let next_head = if self.head + 1 == len {
0
} else {
self.head + 1
};
let tracked cell_perm: Option<cell::PointsTo<T>>;
let tail =
atomic_with_ghost!(&queue.tail => load();
returning tail;
ghost tail_token => {
cell_perm = if self.head as u64 != tail {
let tracked (_, Tracked(cp)) = queue.instance.borrow().consume_start(&tail_token, self.consumer.borrow_mut());
Option::Some(cp)
} else {
Option::None
};
}
);
if self.head as u64 != tail {
let tracked mut cell_perm = match cell_perm {
Option::Some(cp) => cp,
Option::None => {
assert(false);
proof_from_false()
},
};
let t = queue.buffer[self.head].take(Tracked(&mut cell_perm));
atomic_with_ghost!(&queue.head => store(next_head as u64); ghost head_token => {
queue.instance.borrow().consume_end(cell_perm,
cell_perm, &mut head_token, self.consumer.borrow_mut());
});
self.head = next_head;
return t;
}
}
}
}
fn main() {
let (mut producer, mut consumer) = new_queue(20);
// Simple test:
producer.enqueue(5);
producer.enqueue(6);
producer.enqueue(7);
let x = consumer.dequeue();
print_u64(x);
let x = consumer.dequeue();
print_u64(x);
let x = consumer.dequeue();
print_u64(x);
// Multi-threaded test:
let producer = producer;
let _join_handle = vstd::thread::spawn(
move ||
{
let mut producer = producer;
let mut i = 0;
while i < 100
invariant
producer.wf(),
{
producer.enqueue(i);
i = i + 1;
}
},
);
let mut i = 0;
while i < 100
invariant
consumer.wf(),
{
let x = consumer.dequeue();
print_u64(x);
i = i + 1;
}
}
} // verus!Reference-counted smart pointer, tutorial
Our next example is a reference-counted smart pointer like
Rc.
We’re going to focus on 4 functions: new, clone, and drop, and borrow.
The clone and drop functions will be incrementing and decrementing
the reference count, and drop will be responsible for freeing memory when
the count hits zero.
Meanwhile, the borrow function provides access to the underlying data.
Recall that since Rc is a shareable pointer, the underlying data must be
accessed via shared pointer.
type Rc<T>
impl<T> Rc<T> {
pub spec fn view(&self) -> T;
pub fn new(t: T) -> (rc: Self)
ensures rc@ === t
pub fn clone(&self) -> (rc: Self)
ensures rc@ === self@
pub fn drop(self)
pub fn borrow(&self) -> (t: &T)
ensures *t === self@
}In terms of specification, the view() interpretation of an Rc<T> object
will simply be the underlying T, as is reflected in the post-conditions above.
NOTE: A current limitation, at the time of writing, is that
Verus doesn’t yet have proper support for Drop,
so the drop function of our Rc here needs to be called manually to avoid
memory leaks.
Unverified implementation
As usual, we’ll start with an unverified implementation.
// Ordinary Rust code, not Verus
struct InnerRc<T> {
rc_cell: std::cell::UnsafeCell<u64>,
t: T,
}
struct Rc<T> {
ptr: *mut InnerRc<T>,
}
impl<T> Rc<T> {
fn new(t: T) -> Self {
// Allocate a new InnerRc object, initialize the counter to 1,
// and return a pointer to it.
let rc_cell = std::cell::UnsafeCell::new(1);
let inner_rc = InnerRc { rc_cell, t };
let ptr = Box::leak(Box::new(inner_rc));
Rc { ptr }
}
fn clone(&self) -> Self {
unsafe {
// Increment the counter.
// If incrementing the counter would lead to overflow, then abort.
let inner_rc = &*self.ptr;
let count = *inner_rc.rc_cell.get();
if count == 0xffffffffffffffff {
std::process::abort();
}
*inner_rc.rc_cell.get() = count + 1;
}
// Return a new Rc object with the same pointer.
Rc { ptr: self.ptr }
}
fn drop(self) {
unsafe {
// Decrement the counter.
let inner_rc = &*self.ptr;
let count = *inner_rc.rc_cell.get() - 1;
*inner_rc.rc_cell.get() = count;
// If the counter hits 0, drop the `T` and deallocate the memory.
if count == 0 {
std::ptr::drop_in_place(&mut (*self.ptr).t);
std::alloc::dealloc(self.ptr as *mut u8, std::alloc::Layout::for_value(&*self.ptr));
}
}
}
fn borrow(&self) -> &T {
unsafe { &(*self.ptr).t }
}
}
// Example usage
enum Sequence<V> {
Nil,
Cons(V, Rc<Sequence<V>>),
}
fn main() {
let nil = Rc::new(Sequence::Nil);
let nil_clone = nil.clone();
let a5 = Rc::new(Sequence::Cons(5, nil.clone()));
let a7 = Rc::new(Sequence::Cons(7, nil.clone()));
let a67 = Rc::new(Sequence::Cons(6, a7.clone()));
let x1 = nil.borrow();
let x2 = nil_clone.borrow();
match x1 {
Sequence::Nil => {}
Sequence::Cons(_, _) => {
assert!(false);
}
}
match x2 {
Sequence::Nil => {}
Sequence::Cons(_, _) => {
assert!(false);
}
}
nil.drop();
nil_clone.drop();
a5.drop();
a7.drop();
a67.drop();
}Verified implementation
The main challenge here is to figure out what structure the ghost code will take.
- We need a “something” that will let us get the
&PointsToobject that we need to dereference the pointer. This has to be a shared reference by necessity. - The “something” needs to be duplicateable somehow; we need to obtain a new one whenever
we call
Rc::clone.- The counter, somehow, needs to correspond to the number of “somethings” in existence. In other words, we should be able to get a new “something” when we increment the counter, and we should destroy a “something” when we decrement it.
- We need a way to obtain ownership of the the
PointsToobject for thePCellstoring the counter, so that we can write to it.
Let’s stop being coy and name the ghost components. The “something” is the driver of action
here, so let’s go ahead and call it a ref.
Let’s have another ghost object called a counter—the counter counts the refs.
The ghost counter needs to be tied to the actual u64 counter,
which we will do with a LocalInvariant.
Therefore, an Rc ought to have:
- A
refobject, which will somehow let us obtain access a&ptr::PointsTo<InnerRc>. - A
LocalInvariantstoring both acounterand acell::PointsTo<u64>.
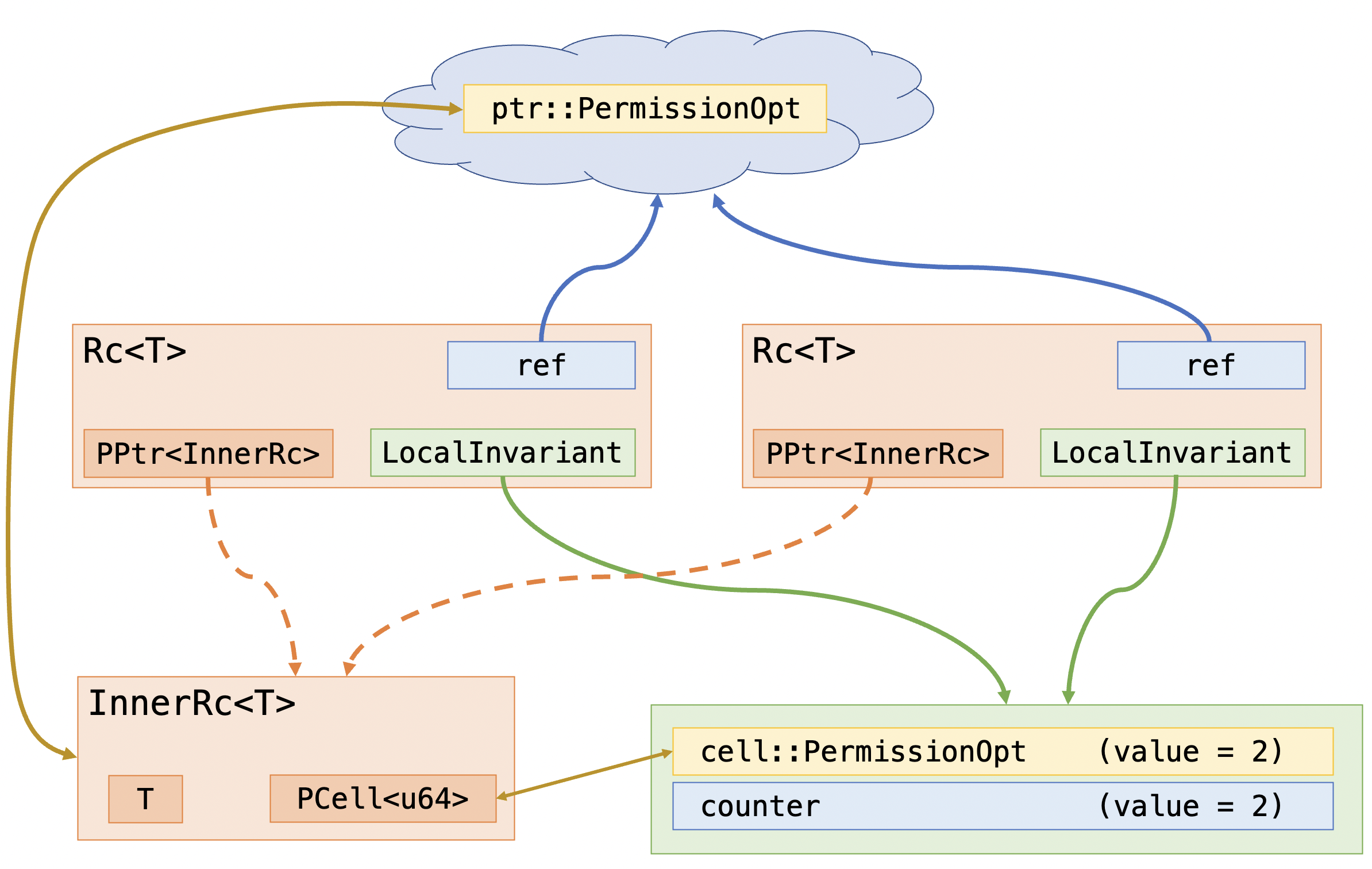
Now, with this rough plan in place, we can finally begin devising our tokenized_state_machine
to define the ref and counter tokens along with the relationship between the
ref token and the ptr::PointsTo.
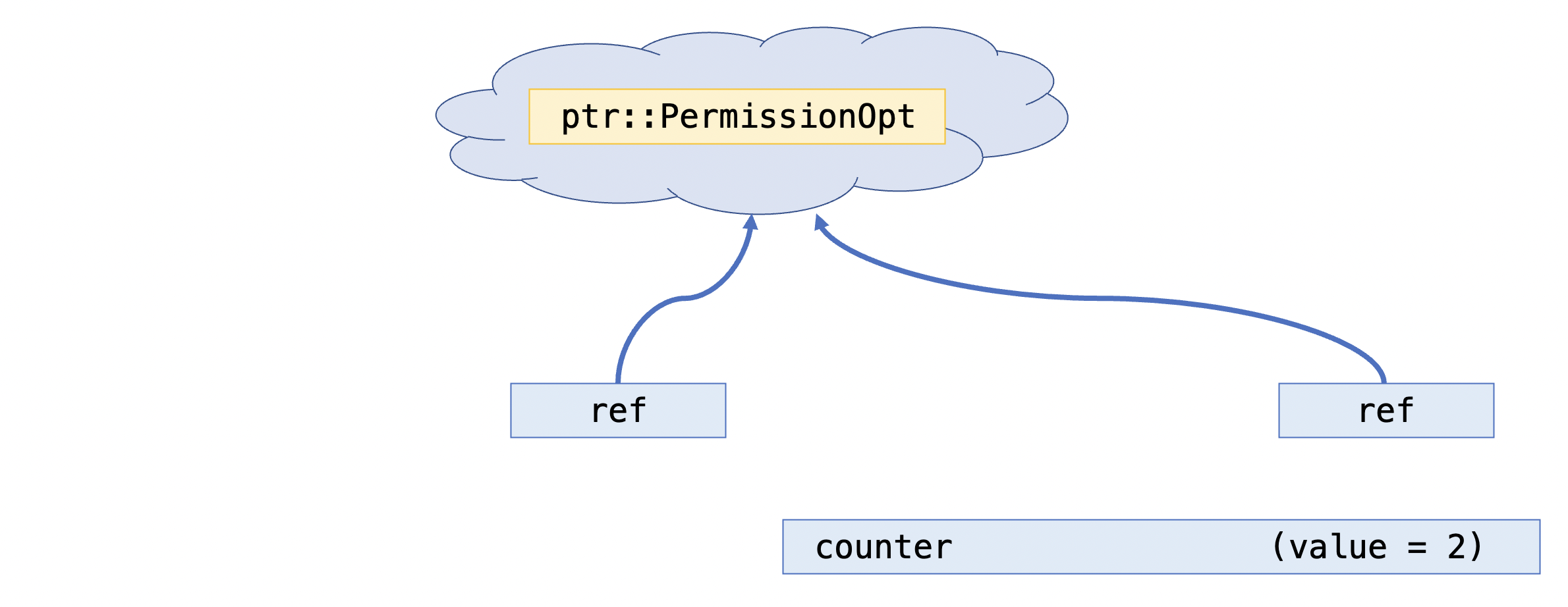
tokenized_state_machine!(RefCounter<Perm> {
fields {
#[sharding(variable)]
pub counter: nat,
#[sharding(storage_option)]
pub storage: Option<Perm>,
#[sharding(multiset)]
pub reader: Multiset<Perm>,
}TODO - finish the rest of this tutorial
Reference-counted smart pointer, unverified Rust source
// Ordinary Rust code, not Verus
struct InnerRc<T> {
rc_cell: std::cell::UnsafeCell<u64>,
t: T,
}
struct Rc<T> {
ptr: *mut InnerRc<T>,
}
impl<T> Rc<T> {
fn new(t: T) -> Self {
// Allocate a new InnerRc object, initialize the counter to 1,
// and return a pointer to it.
let rc_cell = std::cell::UnsafeCell::new(1);
let inner_rc = InnerRc { rc_cell, t };
let ptr = Box::leak(Box::new(inner_rc));
Rc { ptr }
}
fn clone(&self) -> Self {
unsafe {
// Increment the counter.
// If incrementing the counter would lead to overflow, then abort.
let inner_rc = &*self.ptr;
let count = *inner_rc.rc_cell.get();
if count == 0xffffffffffffffff {
std::process::abort();
}
*inner_rc.rc_cell.get() = count + 1;
}
// Return a new Rc object with the same pointer.
Rc { ptr: self.ptr }
}
fn drop(self) {
unsafe {
// Decrement the counter.
let inner_rc = &*self.ptr;
let count = *inner_rc.rc_cell.get() - 1;
*inner_rc.rc_cell.get() = count;
// If the counter hits 0, drop the `T` and deallocate the memory.
if count == 0 {
std::ptr::drop_in_place(&mut (*self.ptr).t);
std::alloc::dealloc(self.ptr as *mut u8, std::alloc::Layout::for_value(&*self.ptr));
}
}
}
fn borrow(&self) -> &T {
unsafe { &(*self.ptr).t }
}
}
// Example usage
enum Sequence<V> {
Nil,
Cons(V, Rc<Sequence<V>>),
}
fn main() {
let nil = Rc::new(Sequence::Nil);
let nil_clone = nil.clone();
let a5 = Rc::new(Sequence::Cons(5, nil.clone()));
let a7 = Rc::new(Sequence::Cons(7, nil.clone()));
let a67 = Rc::new(Sequence::Cons(6, a7.clone()));
let x1 = nil.borrow();
let x2 = nil_clone.borrow();
match x1 {
Sequence::Nil => {}
Sequence::Cons(_, _) => {
assert!(false);
}
}
match x2 {
Sequence::Nil => {}
Sequence::Cons(_, _) => {
assert!(false);
}
}
nil.drop();
nil_clone.drop();
a5.drop();
a7.drop();
a67.drop();
}Reference-counted smart pointer, verified source
use verus_builtin::*;
use verus_builtin_macros::*;
use verus_state_machines_macros::tokenized_state_machine;
use vstd::cell::*;
use vstd::invariant::*;
use vstd::modes::*;
use vstd::multiset::*;
use vstd::prelude::*;
use vstd::simple_pptr::*;
use vstd::{pervasive::*, *};
use vstd::shared::*;
verus! {
tokenized_state_machine!(RefCounter<Perm> {
fields {
#[sharding(variable)]
pub counter: nat,
#[sharding(storage_option)]
pub storage: Option<Perm>,
#[sharding(multiset)]
pub reader: Multiset<Perm>,
}
#[invariant]
pub fn reader_agrees_storage(&self) -> bool {
forall |t: Perm| self.reader.count(t) > 0 ==>
self.storage == Option::Some(t)
}
#[invariant]
pub fn counter_agrees_storage(&self) -> bool {
self.counter == 0 ==> self.storage is None
}
#[invariant]
pub fn counter_agrees_storage_rev(&self) -> bool {
self.storage is None ==> self.counter == 0
}
#[invariant]
pub fn counter_agrees_reader_count(&self) -> bool {
self.storage is Some ==>
self.reader.count(self.storage->0) == self.counter
}
init!{
initialize_empty() {
init counter = 0;
init storage = Option::None;
init reader = Multiset::empty();
}
}
#[inductive(initialize_empty)]
fn initialize_empty_inductive(post: Self) { }
transition!{
do_deposit(x: Perm) {
require(pre.counter == 0);
update counter = 1;
deposit storage += Some(x);
add reader += {x};
}
}
#[inductive(do_deposit)]
fn do_deposit_inductive(pre: Self, post: Self, x: Perm) { }
property!{
reader_guard(x: Perm) {
have reader >= {x};
guard storage >= Some(x);
}
}
transition!{
do_clone(x: Perm) {
have reader >= {x};
add reader += {x};
update counter = pre.counter + 1;
}
}
#[inductive(do_clone)]
fn do_clone_inductive(pre: Self, post: Self, x: Perm) {
assert(pre.reader.count(x) > 0);
assert(pre.storage == Option::Some(x));
assert(pre.storage is Some);
assert(pre.counter > 0);
}
transition!{
dec_basic(x: Perm) {
require(pre.counter >= 2);
remove reader -= {x};
update counter = (pre.counter - 1) as nat;
}
}
transition!{
dec_to_zero(x: Perm) {
remove reader -= {x};
require(pre.counter < 2);
assert(pre.counter == 1);
update counter = 0;
withdraw storage -= Some(x);
}
}
#[inductive(dec_basic)]
fn dec_basic_inductive(pre: Self, post: Self, x: Perm) {
assert(pre.reader.count(x) > 0);
assert(pre.storage == Option::Some(x));
}
#[inductive(dec_to_zero)]
fn dec_to_zero_inductive(pre: Self, post: Self, x: Perm) { }
});
pub struct InnerRc<S> {
pub rc_cell: PCell<u64>,
pub s: S,
}
pub type MemPerms<S> = simple_pptr::PointsTo<InnerRc<S>>;
pub tracked struct GhostStuff<S> {
pub tracked rc_perm: cell::PointsTo<u64>,
pub tracked rc_token: RefCounter::counter<MemPerms<S>>,
}
impl<S> GhostStuff<S> {
pub open spec fn wf(self, inst: RefCounter::Instance<MemPerms<S>>, cell: PCell<u64>) -> bool {
&&& self.rc_perm@.pcell == cell.id()
&&& self.rc_token.instance_id() == inst.id()
&&& self.rc_perm.is_init()
&&& self.rc_perm.value() as nat == self.rc_token.value()
}
}
impl<S> InnerRc<S> {
spec fn wf(self, cell: PCell<u64>) -> bool {
self.rc_cell == cell
}
}
struct_with_invariants!{
struct MyRc<S> {
pub inst: Tracked< RefCounter::Instance<MemPerms<S>> >,
pub inv: Tracked< Shared<LocalInvariant<_, GhostStuff<S>, _>> >,
pub reader: Tracked< RefCounter::reader<MemPerms<S>> >,
pub ptr: PPtr<InnerRc<S>>,
pub rc_cell: Ghost< PCell<u64> >,
}
spec fn wf(self) -> bool {
predicate {
&&& self.reader@.element().pptr() == self.ptr
&&& self.reader@.instance_id() == self.inst@.id()
&&& self.reader@.element().is_init()
&&& self.reader@.element().value().rc_cell == self.rc_cell
}
invariant on inv with (inst, rc_cell)
specifically (self.inv@@)
is (v: GhostStuff<S>)
{
v.wf(inst@, rc_cell@)
}
}
}
impl<S> MyRc<S> {
spec fn view(self) -> S {
self.reader@.element().value().s
}
fn new(s: S) -> (rc: Self)
ensures
rc.wf(),
rc@ == s,
{
let (rc_cell, Tracked(rc_perm)) = PCell::new(1);
let inner_rc = InnerRc::<S> { rc_cell, s };
let (ptr, Tracked(ptr_perm)) = PPtr::new(inner_rc);
let tracked (Tracked(inst), Tracked(mut rc_token), _) =
RefCounter::Instance::initialize_empty(Option::None);
let tracked reader = inst.do_deposit(
ptr_perm,
&mut rc_token,
ptr_perm,
);
let tracked g = GhostStuff::<S> { rc_perm, rc_token };
let tr_inst = Tracked(inst);
let gh_cell = Ghost(rc_cell);
let tracked inv = LocalInvariant::new((tr_inst, gh_cell), g, 0);
let tracked inv = Shared::new(inv);
MyRc { inst: tr_inst, inv: Tracked(inv), reader: Tracked(reader), ptr, rc_cell: gh_cell }
}
fn borrow<'b>(&'b self) -> (s: &'b S)
requires
self.wf(),
ensures
*s == self@,
{
let tracked inst = self.inst.borrow();
let tracked reader = self.reader.borrow();
let tracked perm = inst.reader_guard(reader.element(), &reader);
&self.ptr.borrow(Tracked(perm)).s
}
fn clone(&self) -> (s: Self)
requires
self.wf(),
ensures
s.wf() && s@ == self@,
{
let tracked inst = self.inst.borrow();
let tracked reader = self.reader.borrow();
let tracked perm = inst.reader_guard(reader.element(), &reader);
let inner_rc_ref = self.ptr.borrow(Tracked(perm));
let tracked new_reader;
open_local_invariant!(self.inv.borrow().borrow() => g => {
let tracked GhostStuff { rc_perm: mut rc_perm, rc_token: mut rc_token } = g;
let count = inner_rc_ref.rc_cell.take(Tracked(&mut rc_perm));
assume(count < 100000000);
let count = count + 1;
inner_rc_ref.rc_cell.put(Tracked(&mut rc_perm), count);
proof {
new_reader = self.inst.borrow().do_clone(
reader.element(),
&mut rc_token,
&reader);
}
proof { g = GhostStuff { rc_perm, rc_token }; }
});
MyRc {
inst: Tracked(self.inst.borrow().clone()),
inv: Tracked(self.inv.borrow().clone()),
reader: Tracked(new_reader),
ptr: self.ptr,
rc_cell: Ghost(self.rc_cell@),
}
}
fn dispose(self)
requires
self.wf(),
{
let MyRc {
inst: Tracked(inst),
inv: Tracked(inv),
reader: Tracked(reader),
ptr,
rc_cell: _,
} = self;
let tracked perm = inst.reader_guard(reader.element(), &reader);
let inner_rc_ref = &ptr.borrow(Tracked(perm));
let count;
let tracked mut inner_rc_perm_opt = None;
open_local_invariant!(inv.borrow() => g => {
let tracked GhostStuff { rc_perm: mut rc_perm, rc_token: mut rc_token } = g;
count = inner_rc_ref.rc_cell.take(Tracked(&mut rc_perm));
if count >= 2 {
let count = count - 1;
inner_rc_ref.rc_cell.put(Tracked(&mut rc_perm), count);
proof {
inst.dec_basic(
reader.element(),
&mut rc_token,
reader);
}
} else {
let tracked mut inner_rc_perm = inst.dec_to_zero(
reader.element(),
&mut rc_token,
reader);
let inner_rc = ptr.take(Tracked(&mut inner_rc_perm));
// we still have to write back to the `inner_rc` to restore the invariant
// even though inner_rc has been moved onto the stack here.
// so this will probably get optimized out
let count = count - 1;
inner_rc.rc_cell.put(Tracked(&mut rc_perm), count);
proof {
inner_rc_perm_opt = Some(inner_rc_perm);
}
}
proof { g = GhostStuff { rc_perm, rc_token }; }
});
if count < 2 {
ptr.free(Tracked(inner_rc_perm_opt.tracked_unwrap()));
}
}
}
enum Sequence<V> {
Nil,
Cons(V, MyRc<Sequence<V>>),
}
fn main() {
let nil = MyRc::new(Sequence::Nil);
let a5 = MyRc::new(Sequence::Cons(5, nil.clone()));
let a7 = MyRc::new(Sequence::Cons(7, nil.clone()));
let a67 = MyRc::new(Sequence::Cons(6, a7.clone()));
}
} // verus!Exercises
-
Implement a thread-safe reference-counted pointer,
Arc. TheArc<T>typed should satisfy theSendandSyncmarker traits.Answer the following:
(a) In terms of executable code, which part of
Rcis not thread-safe? How does it need to change?(b) In terms of ghost code, which component prevents
Rcfrom satisfyingSendorSync? What should it be changed to to supportSendandSync?(c) In order to make change (b), it is necessary to also make change (a). Why?
-
Augment the verified
Rcto allow weak pointers. The allocation should include 2 counts: a strong reference count (as before) and a weak reference count. The innerTis dropped when the strong reference count hits 0, but the memory is not freed until both counts hit 0. Upgrading a weak pointer should fail in the case that the strong count has already hit 0.Implement the above and verify a spec like the following:
type Rc<T>
type Weak<T>
impl<T> Rc<T> {
pub spec fn view(&self) -> T;
pub fn new(t: T) -> (rc: Self)
ensures rc@ === t
pub fn clone(&self) -> (rc: Self)
ensures rc@ === self@
pub fn drop(self)
pub fn borrow(&self) -> (t: &T)
ensures *t === self@
pub fn downgrade(&self) -> (weak: Weak<T>)
ensures weak@ === self@
}
impl<T> Weak<T> {
pub spec fn view(&self) -> T;
pub fn clone(&self) -> (weak: Self)
ensures weak@ === self@
pub fn drop(self)
pub fn upgrade(&self) -> (rc_opt: Option<Rc<T>>)
ensures match rc_opt {
None => true,
Some(rc) => rc@ === self@,
}
}Guide (TODO)
Counting to n (again) (TODO)
Hash table (TODO)
Reader-writer lock (TODO)
State Machine Basics
Components of a State Machine
The state_machines_macros library provides two macros, state_machine! and tokenized_state_machine!. This overview will discuss the first.
The state_machine! framework provides a way to establish a basic state machine, consisting of four components:
- The state definition
- The transitions (including initialization procedures)
- Invariants on the state
- Proofs that the invariants hold
Here’s a very simple example:
state_machine!{
AdderMachine {
//// The state definition
fields {
pub number: int,
}
//// The transitions
init!{
initialize() {
init number = 0;
}
}
transition!{
add(n: int) {
update number = pre.number + 2*n;
}
}
//// Invariants on the state
#[invariant]
pub fn is_even(&self) -> bool {
self.number % 2 == 0
}
//// Proofs that the invariants hold
#[inductive(initialize)]
fn initialize_inductive(post: Self) {
// Verus proves that 0 % 2 == 0
}
#[inductive(add)]
fn add_inductive(pre: Self, post: Self, n: int) {
// Verus proves that if `pre.number % 2 == 0` then
// `post.number` is `pre.number + 2*n` is divisble by 2 as well.
}
}
}State
The state definition is given inside a block labelled fields (a special keyword recognized by the state_machine! macro):
fields {
pub number: int,
}The fields are like you’d find in a struct: they must be named fields (i.e., there’s no “tuple” option for the state). The fields are also implicitly #[spec].
Transitions
There are four different types of “operations”: init!, transition!, readonly!, and property!. The body of the operation is a “transition DSL” which is interpretted by the macro:
- An
init!becomes a 1-state relation representing valid initial states of the system - A
transition!becomes a 2-state relation representing a transition from one state (pre) to the next (post) - A
readonly!becomes a 2-state relation where the state cannot be modified. - A
property!allows the user to add safety conditions on a single state (pre).
When exported as relations:
- 1-state
init!operations take 1 argument,pre. - 2-state operations (
transition!andreadonly!) take 2 arguments,preandpost. property!operations are not exported as relations.
Each operation (transition or otherwise) is deterministic in its input arguments, so any intended non-determinism should be done via the arguments.
The DSL allows the user to update fields; any field not updated is implied to remain the same.
An init! transition is required to initialize each field, so that the intialization is fully determined.
The DSL provides four fundamental operations (init, update, require, assert)
as detailed in the transition language reference.
They are allowed according to the following table:
init! | transition! | readonly! | property! | |
|---|---|---|---|---|
init | yes | |||
update | yes | |||
require | yes | yes | yes | yes |
assert | yes | yes | yes |
The distinction between readonly! and property! is somewhat pedantic: after all,
both are expressed as predicates on states which are not modified, and both
allow require and assert statements.
The difference is that
a readonly! operation is exported as an actual transition between pre and post
(with pre === post) whereas a property! is not exported as a transition.
Invariants
See the documentation for invariants.
State Machine Macro Syntax (TODO)
Transition Language
All four operations (init!, transition!, readonly! and property!) use
the transition language (although property! operations are not technically transitions).
The operations can be declared like so:
transition!{
name(params...) {
TransitionStmt
}
}The TransitionStmt language allows very simple control-flow with if-else and match
statements, and allows let-bindings.
TransitionStmt :=
| TransitionStmt; TransitionStmt;
| if $expr { TransitionStmt }
| if $expr { TransitionStmt } else { TransitionStmt }
| match $expr { ( $pat => { TransitionStmt } )* }
| let $pat = $expr;
| SingleStmtThere are four fundamental statements: init, update, require, and assert.
For convenience, there are also higher-level statements that can be expressed
in those terms.
SingleStmt :=
| init $field_name = $expr;
| update $field_name = $expr;
| require $bool_expr;
| assert $bool_expr (by { ... })? ;
// Higher-level statements:
| require let $pat = $expr;
| assert let $pat = $expr;
| update $field_name ([sub_idx] | .subfield)* = $expr;
| remove ... | have ... | add ... | deposit ... | guard ... | withdraw ...Each $field_name should be a valid field name as declared in the fields block of the state machine definition.
Each $expr/$bool_expr is an ordinary Verus (spec-mode) expression.
These expressions can reference the params or bound variables.
They can also reference the pre-state of the transition, pre (except in init! operations).
(Note that it is not possible to access post directly,
though this may be added in the future.)
Core statements
The init statement
The init statement is used only in init! operations.
Each field of the state must be initialized exactly once in each init! operation.
If there is any control-flow-branching, then each field must be initialized
exactly once in each branch.
Example:
state_machine!{ InitExample {
fields {
pub x: int,
pub y: int,
}
// Okay.
init!{
initialize_1(x_init_value: int) {
init x = x_init_value;
init y = 0;
}
}
// Not okay (y is not initialized)
init!{
initialize_2(x_init_value: int) {
init x = x_init_value;
}
}
// Not okay (y is not initialized in the second branch)
init!{
initialize_3(b: bool) {
if b {
init x = 0;
init y = 1;
} else {
init x = 5;
}
}
}
}}The update statement
The update statement is the counterpart of init for the transition! operations:
it sets the value of a field for a post state.
However, (unlike init), not every field needs to be updated.
Any field for which no update statement appears will implicitly maintain its value
from the pre state.
Example:
state_machine!{ TransitionExample {
fields {
pub x: int,
pub y: int,
}
// Okay.
transition!{
transition_1(x_new_value: int) {
update x = x_new_value;
}
}
// Okay.
transition!{
transition_2(b: bool) {
if b {
update x = 0;
update y = 1;
} else {
update x = 5;
}
}
}
// Not okay.
// (The first 'update' is meaningless because it is immediately overwritten.)
transition!{
transition_3(b: bool) {
update x = 0;
update x = 1;
}
}
}}The require statement
The require statement adds an enabling condition to the operation.
This is a condition that must hold in order for the operation to be performed.
A require can be used in any of the operation types.
The assert statement
The assert statement declares a safety condition on the transition. Verus creates a proof obilgation for the validity of the state machine: the assert must follow from the state invariants, and from any enabling conditions (require statements) given prior to the assert.
If the user needs to provide manual proofs, they can do so using an assert-by:
assert $bool_expr by {
/* proof here */
};(TODO need a better example here)
Because we demand that the assert statement is proved,
clients of the state machine may assume that the condition holds whenever the transition is enabled (i.e., all its require conditions hold).
other proofs can assume that the predicate holds whenever this transition is enabled.
Therefore, the assert statement is not itself an enabling condition; that is, clients do not need to show the condition holds in order to show that the operation is enabled.
High-level statements
require let and assert let
You can write,
require let $pat = $expr;where $pat is a refutable pattern.
This is roughly equivalent to writing the following (which would ordinarily be disallowed
because of the refutable pattern).
require ($expr matches $pat);
let $pat = $expr;The assert let statement is similar, but for assert instead of require.
Example:
state_machine!{ RequireLetExample {
fields {
x_opt: Option<int>,
}
transition!{
add_1() {
require let Some(x) = pre.x_opt;
update x_opt = Some(x + 1);
}
}
// Equivalent to:
transition!{
add_1_alternative() {
require pre.x_opt is Some;
let x = pre.x_opt->0;
update x_opt = Some(x + 1);
}
}
}}Update with subscript and fields
Note: This feature is currently in-development.
To update nested data structures, you can use fields (for structs)
or subscripts (for maps or sequences) in update statements.
For example,
update field.x.y[idx].z[key] = expr;remove / have / add / deposit / guard / withdraw
These are complex operations used specially for specific sharding strategies
in a tokenized_state_machine.
See the strategy reference for details.
Invariants
An invariant on a transition system is a boolean predicate that must hold on any
reachable state of the system—i.e., a state reachable by starting at any init
and then executing a sequence of transitions.
Verus allows the user to specify an inductive invariant, that is, a predicate that must satisfy the inductive criteria:
init(state) ==> inv(state)transition(pre, post) && inv(pre) ==> inv(post)
By induction, any predicate satisfying the above criteria is necessarily a valid invariant that holds for any reachable state.
There are many reasons the user might need to specify (and prove correct) such an invariant:
-
The invariant is needed to prove the safety conditions of the state machine, that is, the
assertstatements that appear in any transitions or properties. -
The invariant is needed to prove a state machine refinement.
Specifying the invariants
To make it easier to name individual clauses of the inductive invariant,
they are given as boolean predicates with #[invariant] attributes.
The boolean predicates should take a single argument, &self.
#[invariant]
pub fn inv_1(&self) -> bool { ... }
#[invariant]
pub fn inv_2(&self) -> bool { ... }The state machine macro produces a single predicate invariant which is the conjunct of all the given invariants.
Proving the inductive criteria
To prove that the invariants are correct,
the user needs to prove that every init! operation results in a state satisfying
the invariant, and that every transition! operation preserves the invariant
from one state to the next.
This is done by creating a lemma to contain the proof and annotating
it with the inductive attribute:
// For an `init!` routine:
#[inductive(init_name)]
fn initialize_inductive(post: Self) {
// Proof here
}
// For a `transition!` routine:
#[inductive(transition_name)]
fn transition_inductive(pre: Self, post: Self, n: int) {
// Proof here
} Verus requires one lemma for each init! and transition! routine, provided at least
one invariant predicate is specified.
(The lemma would be trivial for a readonly! transition, so for these, it is not required.)
- For an
init!operation, the lemma parameters should always bepost: Self, ...where the...are the custom arguments to the transition. - For a
transition!operation, the lemma parameters should always bepre: Self, post: Self, ....
If the lemmas are omitted, then the Verus error will provide the expected type signatures in the console output.
Pre- and post-conditions for each lemma are automatically generated, so these should be left off. Specifically, the macro generates the following conditions:
// For an `init!` routine:
#[inductive(init_name)]
fn initialize_inductive(post: StateName, ...) {
requires(init(post, ...));
ensures(post.invariant());
// ... The user's proof is placed here
}
// For a `transition!` routine:
#[inductive(transition_name)]
fn transition_inductive(pre: StateName, post: StateName, ...) {
requires(strong_transition(pre, post, ...) && pre.invariant());
ensures(post.invariant());
// ... The user's proof is placed here
}Here, init and strong_transition refer to the relations generated from the DSL.
These contain all the predicates from the require statements defined in the transition or initialization routine.
The strong indicates that we can assume the conditions given by any assert statements in addition to the require statements.
(Proof obligations for the assert statements are generated separately.)
Example
(TODO should have an example)
Macro-generated code
State Machine Refinements
Tokenization
Strategy Reference
In a tokenized state machine, Verus produces a set of token types such that any state of the system represents some collection of objects of those types. This tokenization process is determined by a strategy declared on each field of the state definition. Specifically, for each field, Verus (potentially) generates a token type for the field depending on the declared strategy, with the strategy determining some relationship between the state’s field value and a collection of such tokens. The entire state, consisting of all fields, then corresponds to a collection of objects out of all the defined token types.
-
For example, consider a field
fof typeTwith strategyvariable. In this case, the token type (namedf) has a valueTon it, and we require the collection to always have exactly one such token, giving, of course, the value off. -
On the other hand, consider a field
gof typeMap<K, V>with strategymap. In this case, the token types have pairs(k, v). The collection can have any number of tokens, although they have to all have distinct keys, and the pairs all together form a map which gives the value of fieldg. -
Or consider a field
hof typeOption<V>with strategyoption. In this case, the token type has a valuev: V, and the collection must contain either no tokens for this type (yieldingOption::None), or exactly one (yieldingOption::Some(v)).
Each transition of the system can be viewed both as a transition relation in the same sense as in an orindary transition, but also as an “exchange” of tokens, where a sub-collection of tokens is taken in (consumed) and exchanged for a new sub-collection. All of the rules we discuss below are meant to ensure that each exchange performed on a valid collection will result in another valid collection and that the corresponding global system states transition according to the relation.
The Instance token and the constant strategy
Every tokenized state machine generates a special Instance token type.
Besides serving as a convenient object with which to serve the exchange function API,
the Instance also serves as “unique identifier” for a given instantiation of the protocol.
All other token types have an instance: Instance field, and in any exchange, all
of these instance markers are required to match.
The Instance type implements Clone, so it can be freely shared by all the clients
that need to manipulate some aspect of the protocol.
The Instance type also contains all fields declared with the constant strategy,
accessed as instance.field_name(). Fields with the constant strategy cannot be updated
after the protocol has been initialized, so this information will never be inconsistent.
Furthermore, constant fields do not not generate their own constant types.
The variable strategy
If a field f has strategy variable, then Verus generates a token type f, with values
given by token![$instance => f => $value].
Verus enforces that there is always exactly one token of the type f.
(Technical note: the reader might wonder what happens if the user attempts to drop the token.
This is allowed because dropped tokens are still considered to “exist” in the perspective of the abstract ghost program. Dropping a token only means that it is made inaccessible.)
The value of a variable field is manipulated using the ordinary update command, as in
ordinary transition definitions. The old value can be accessed as usual with pre.f.
If f is updated by a transition, then the corresponding exchange function takes an f
taken as an &mut argument. If f is read (via pre.f) but never updated, then it is
read as an & argument.
If the field is neither read nor written by the transition, then it is not taken as
an argument.
The “collection-style” strategies with remove/have/add
(TODO not all of these exist yet)
A large number of tokenization strategies are specified in what we call collection-style
or monoid-style. Specifically, this includes
option, map, multiset, set, count, and bool,
as well as their “persistent” verions
persistent_option, persistent_map, persistent_set, persistent_count, and persistent_bool.
Basic Collection Strategies
| Strategy | Type | Token value | Requirements / relationship to field value |
|---|---|---|---|
| option | Option<V> | token![$instance => f => $v] | No token for None, one token for Some(v). |
| map | Map<K, V> | token![$instance => f => $k => $v] | At most one token for any given value of k. |
| multiset | Multiset<V> | token![$instance => f => $v] | No restrictions. |
| set | Set<V> | token![$instance => f => $v] | At most one token for any given value of v. |
| count | nat | token![$instance => f => $n] | Any number of tokens; the sum of all tokens gives the field value. |
| bool | bool | token![$instance => f => true] | Token either exists (for true) or doesn’t exist (for false). |
(In the table, v has type V, k has type K, n has type nat, and b has type bool.)
Initially, some of these might seem odd—why, for example, does bool have a true token, and no false token?
However, if the user wants a false token, they can just use the variable strategy. Instead, bool, here, is meant to
represent the case where we want a token that either exists, or doesn’t, with no other information, and the natural
representation of such a thing is a bool. (Actually, bool is just isomorphic to Option<()>.)
Describing transitions for these collection types is somewhat more involved. Note that a user cannot in general
establish the exact value of one of these fields simply by providing some tokens for the field, since it’s always possible
that there are other tokens elsewhere. As such, the values of these fields are not manipulated through update but through
three commands called remove, have, and add.
To describe these, we will first establish a notion of composition on the field types.
Specifically, we define the composition a · b by the idea that if a and b each represent some collection
of tokens, then a · b should represent the union of those two collections.
Of course, this may not always be well defined: as we have discussed, not all possible collections of tokens
are valid collections for the given strategy. Thus, we let a ## b indicate that the composition is well-defined.
(Note: these operators are for documentation purposes only; currently, they are not operators that can be used in Verus code.)
| Strategy | a ## b | a · b |
|---|---|---|
| option | a === None || b === None | if a == None { b } else { a } |
| map | a.dom().disjoint(b.dom()) | a.union_prefer_right(b) |
| multiset | true | a.add(b) |
| set | a.disjoint(b) | a.union(b) |
| count | true | a + b |
| bool | !(a && b) | a || b |
Note that despite any apparent asymmetries, a · b is always commutative whenever a ## b, and these definitions
are all consistent with the union of token collections, given by the relationships in the above table.
Now, write a >= b if there exists some value c such that a · c = b.
Note that c is always unique when it exists. (This property is called cancellativity,
and it is not in general true for a monoid; however, it is true for all the ones we consider here.)
When a >= b, let a - b denote that unique value.
Now, with these operators defined, we can give a general meaning for the three transition commands,
remove, have, and add, in terms of require, update, and assert.
| Command | Meaning as transition on state | Meaning for exchange function |
|---|---|---|
remove f -= (x); | require f >= x;update f = f - x; | Input argument, consumed |
have f >= (x); | require f >= x; | Input argument of type &_ |
add f += (x); | assert f ## x;update f = f · x; | Output argument |
Furthermore, for a given field, the commands always go in the order remove before have before add.
There could be multiple, or none, of each one.
The reason is that ordering would not impact the definition of the exchange function; furthermore,
this particular ordering gives the strongest possible relation definition, so it the easiest to work with.
For example, a remove followed by a have will capture the fact the two values used as arguments
must be disjoint by ##.
Unfortunately, the type of the input or output argument is, in general, somewhat complicated,
since it needs to correspond to the value x in the above table, which takes on the same type as the
field.
For example, suppose f and x take on values of type Map<K, V> with the map strategy.
In that case, the token type (named f) represents only a single (key, value) pair of the map,
and the tracked objects passed into or out of the exchange function would need to be
maps of tokens. (TODO link to documentation about using tracked maps)
The same is true of option, set, and multiset.
In the common case, transitions are defined so that arguments in or out are just single tokens
of the token type f, in the form given in the above table.
(The primary exceptions are output arguments of the init routines
or large, bulk transitions that operate on a lot of state.)
The remove, have, and add commands all allows a syntactic shorthand for “singleton” elements:
add f += Some(x)is foroptionadd f += [k => v]is formapsingletonsadd f += {x}is formultisetandsetsingletons
Of course, this applies to remove and have as well.
The general form is add f += (x) as above, with x taking the same type as field f.
(The parentheses are necessary.)
The general form works for all the collection strategies.
Note that there is no “special” form for either count, since the general form
is perfectly suitable for those situations.
Also note that the special forms generate simpler proof obligations, and thus are easier for the SMT solver to handle.
We supply, here, a reference table for all the different possible commands for each strategy:
| Type | Command | Meaning in transition | Exchange Fn Parameter |
|---|---|---|---|
Option<V> | remove f -= Some(v); | require f === Some(v);update f = None; | Input f |
Option<V> | have f >= Some(v); | require f === Some(v); | Input &f |
Option<V> | add f += Some(v); | assert f === None;update f = Some(v); | Output f |
Option<V> | remove f -= (x); | require x === None || f === x;update f = if x === None { f } else { None }; | Input Option<f> |
Option<V> | have f >= (x); | require x === None || f === x; | Input &Option<f> |
Option<V> | add f += (x); | assert f === None || x === None;update f = if x === None { f } else { x }; | Output Option<f> |
Map<K, V> | remove f -= [k => v]; | require f.contains(k) && f.index(k) === v;update f = f.remove(k); | Input f |
Map<K, V> | have f >= [k => v]; | require f.contains(k) && f.index(k) === v; | Input &f |
Map<K, V> | add f += [k => v]; | assert !f.contains(k);update f = f.insert(k, v); | Output f |
Map<K, V> | remove f -= (x); | require x.le(f);update f = f.remove_keys(x.dom()); | Input Map<K, f> |
Map<K, V> | have f >= (x); | require x.le(f); | Input &Map<K, f> |
Map<K, V> | add f += (x); | assert x.dom().disjoint(f.dom();)update f = f.union_prefer_right(x); | Output Map<K, f> |
Multiset<V> | remove f -= {v}; | require f.count(v) >= 1;update f = f.remove(v); | Input f |
Multiset<V> | have f >= {v}; | require f.count(v) >= 1; | Input &f |
Multiset<V> | add f += {v}; | update f = f.insert(v); | Output f |
Multiset<V> | remove f -= (x); | require x.le(f);update f = f.sub(x); | Input Multiset<f> |
Multiset<V> | have f >= (x); | require x.le(f); | Input &Multiset<f> |
Multiset<V> | add f += (x); | update f = f.add(x); | Output Multiset<f> |
Set<V> | remove f -= {v}; | require f.contains(v);update f = f.remove(v); | Input f |
Set<V> | have f >= {v}; | require f.contains(v); | Input &f |
Set<V> | add f += {v}; | assert !f.contains(v);update f = f.insert(v); | Output f |
Set<V> | remove f -= (x); | require x.subset_of(f);update f = f.difference(x); | Input Set<f> |
Set<V> | have f >= (x); | require x.subset_of(f); | Input &Set<f> |
Set<V> | add f += (x); | assert f.disjoin(t);update f = f.union(x); | Output Set<f> |
nat | remove f -= (x); | require f >= x;update f = f - x; | Input f |
nat | have f >= (x); | require f >= x; | Input &f |
nat | add f += (x); | update f = f + x; | Output f |
bool | remove f -= true; | require f == true;update f = false; | Input f |
bool | have f >= true; | require f == true; | Input &f |
bool | add f += true; | assert f == false;update f = true; | Output f |
bool | remove f -= (x); | require x ==> f;update f = f && !x; | Input Option<f> |
bool | have f >= (x); | require x ==> f; | Input &Option<f> |
bool | add f += (x); | assert !(f && x);update f = f || x; | Output Option<f> |
Persistent Collection Strategies
Verus supports “persistent” versions for several of the collection types:
persistent_option, persistent_map, persistent_set, persistent_count, and persistent_bool.
By “persistent”, we mean that any state introduced is permanent.
persistent_option: once a value becomesSome(x), it will always remainSome(x).persistent_map: once a (key, value) pair is inserted, that key will always remain, and its value will never change.persistent_set: once a value is inserted, that value will remainpersistent_count: the number can never decreasepersistent_bool: once it becomes true, it can never become false.
As a result, we can remove the uniqueness constraints on the tokens,
and we can implement Clone on the token type.
In other words, for a given token (say, token![instance => f => k => v])
we can freely make clones of that token without tracking the number of clones.
| Strategy | a ## b | a · b |
|---|---|---|
persistent_option | a === None || b === None || a === b | if a == None { b } else { a } |
persistent_map | a.agrees(b) | a.union_prefer_right(b) |
persistent_set | true | a.union(b) |
persistent_count | true | max(a, b) |
persistent_bool | true | a || b |
Unlike before, a ## a always holds (with a · a = a).
At a technical level,
this property is what makes it safe to implement Clone on the tokens.
This property also lets us see why we cannot remove state.
These monoids are not cancellative like the above; in particular,
if we have state a and attempt
to “subtract” a, then we might still be left with a.
Thus, from the perspective of the transition system, there can never be any point
to doing a remove.
have and add are specified in the same methodology as above, which amounts to the following:
| Type | Command | Meaning in transition | Exchange Fn Parameter |
|---|---|---|---|
Option<V> | have f >= Some(v); | require f === Some(v); | Input &f |
Option<V> | add f += Some(v); | assert f === None || f === Some(v);update f = Some(v); | Output f |
Option<V> | have f >= (x); | require x === None || f === x; | Input &Option<f> |
Option<V> | add f += (x); | assert f === None || x === None || f === x;update f = if x === None { f } else { x }; | Output Option<f> |
Map<K, V> | have f >= [k => v]; | require f.contains(k) && f.index(k) === v; | Input &f |
Map<K, V> | add f += [k => v]; | assert f.contains(k) ==> f.index(k) === v;update f = f.insert(k, v); | Output f |
Map<K, V> | have f >= (x); | require x.le(f); | Input &Map<K, f> |
Map<K, V> | add f += (x); | assert x.agrees(f)update f = f.union_prefer_right(x); | Output Map<K, f> |
Set<V> | have f >= {v}; | require f.contains(v); | Input &f |
Set<V> | add f += {v}; | update f = f.insert(v); | Output f |
Set<V> | have f >= (x); | require x.subset_of(f); | Input &Set<f> |
Set<V> | add f += (x); | update f = f.union(x); | Output Set<f> |
nat | have f >= (x); | require f >= x; | Input &f |
nat | add f += (x); | update f = max(f, x); | Output f |
bool | have f >= true; | require f == true; | Input &f |
bool | add f += true; | update f = true; | Output f |
bool | have f >= (x); | require x ==> f; | Input &Option<f> |
bool | add f += (x); | update f = f || x | Output Option<f> |
Inherent Safety Conditions
Above, we discussed the general meanings of remove, have, and add, which we repeat here
for reference:
| Command | Meaning as transition on state | Meaning for exchange function |
|---|---|---|
remove f -= (x); | require f >= x;update f = f - x; | Input argument, consumed |
have f >= (x); | require f >= x; | Input argument of type &_ |
add f += (x); | assert f ## x;update f = f · x; | Output argument |
The reader may wonder, why do we use assert for add, but not for the other two?
In the case of remove and have, we allow f >= x to be an enabling condition, and it is then
possible for the client of an exchange function to justify that the enabling condition is met by
the existence of the tokens that it inputs.
In the case of add, however, there is no such justification because the tokens that correspond to x
are output tokens. These tokens do not exist before the transition occurs, so we cannot use their
existence to justify the transition is safe. Rather, it is up to the developer of the transition system
to show that introducing the state given by x is always safe. Hence, we use assert to create a safety condition.
We call this the inherent safety condition of the add command.
As with any ordinary assert, the developer is expected to show that it follows from the invariant
and from any preceeding enabling conditions.
If the proof, does not go through automatically, the developer can supply a proof body using by, e.g.,:
add f += Some(v) by {
// proof that pre.f === None
};Init
TODO
Pattern matching with remove and have
The variable strategy
The variable strategy can be applied to fields of any type V.
fields {
#[sharding(variable)]
pub field: V,
}Tokens.
VerusSync creates a fresh token type, tok,
named State::field where State is the name of the VerusSync system and field is the name of the field.
The token type tok implements the
UniqueValueToken<V> trait.
Relationship between global field value and the token. The value of the token is the same as the value of the field. Having multiple such tokens at the same time (for the same field) is an impossible state.
Manipulation of the field
Overview
Unlike with most strategies,
fields of strategy variable are manipulated in the same way as fields of “normal” non-tokenized
state machines, using init and update instructions, and by referring to the value using
pre.field. These fields do not have special associated “tokenized” instructions.
Initializing the field
Initializing the field is done with the usual init statement (as it for all strategies).
init field = v;The instance-init function will return a token of type tok.
Reading the field
Reading the field can be done by writing pre.field. If the variable is read but not modified,
it will be input as a
&tok.
If it’s read and modified, it will be input as a
&mut tok.
Updating the field
Updating the field is done with the update statement in any transition! operation:
update field = v;The token will be input and modified via an argument of type
&mut tok.
Example
TODO
The constant strategy
The constant strategy can be applied to fields of any type V.
fields {
#[sharding(constant)]
pub field: V,
}Tokens.
VerusSync doesn’t create a new token type this field; instead, the constant goes on
the Instance token.
It can be accessed by writing instance.field()
(where field is the field name). Thus, the value of the constant is always accessible
in any token operation.
(If for some reason you really need a separate token type that isn’t on the Instance field,
you can use the persisent_option strategy.
Manipulation of the field
Overview
Unlike with most strategies,
fields of strategy constant are manipulated in the same way as fields of “normal” non-tokenized,
except you can’t update them.
They are initialized using init, and you can read the value in transitions or other operations
by referring to the value using pre.field. These fields do not have special associated “tokenized” instructions.
Initializing the field
Initializing the field is done with the usual init statement (as it for all strategies).
init field = v;The instance-init function will return an instance whose value of the constant
(instance.field()) has value v.
Reading the field
Reading the field can be done by writing pre.field.
Example
TODO
The option strategy
The option strategy can be applied to fields of type Option<V> for any type V.
fields {
#[sharding(option)]
pub field: Option<V>,
}Tokens.
VerusSync creates a fresh token type, tok,
named State::field where State is the name of the VerusSync system and field is the name of the field.
The token type tok implements the
UniqueValueToken<V> trait.
Relationship between global field value and the token.
When field is None, this corresponds to no token existing, while
when field is Some(v), this corresponds to a token of value v existing.
Having multiple such tokens at the same time is an impossible state.
Manipulation of the field
Quick Reference
In the following table, v: V and v_opt: Option<V>.
| Command | Meaning in transition | Exchange Fn Parameter |
|---|---|---|
init field = v_opt; |
init field = v_opt; |
Output Option<tok> |
remove field -= Some(v); |
require field == Some(v);update field = None; |
Input tok |
have field >= Some(v); |
require field == Some(v); |
Input &tok |
add field += Some(v); |
assert field == None;update field = Some(v); |
Output tok |
remove field -= (v_opt); |
require v_opt == None || field == v_opt;
update field = if v_opt == None { field }
else { None }; |
Input Option<tok> |
have field >= (v_opt); |
require v_opt == None || field == v_opt; |
Input &Option<tok> |
add field += (v_opt); |
assert field == None || v_opt == None;
update field = if v_opt == None { field }
else { v_opt }; |
Output Option<tok> |
Initializing the field
Initializing the field is done with the usual init statement (as it for all strategies).
init field = opt_v;The instance-init function will return a token of type Option<tok>,
related as follows:
value of opt_v: Option<V> |
value of optional token Option<tok> |
|---|---|
None |
None |
Some(v) |
Some(tok) where tok.value() == v |
Adding a token
To write an operation that creates a token with value v,
equivalently,
updating the field’s value from None to Some(v), write, inside any transition!
operation:
add field += Some(v);This operation has an inherent safety condition that the prior value of field is None.
The resulting token exchange function will return a token of type tok
and with value v.
If you require manual proof to prove the inherent safety condition, you can add
an optional by clause:
add field += Some(v)
by {
// proof goes here
};Removing a token
To write an operation that removes a token with value v,
equivalently,
updating the field’s value from Some(v) to None, write, inside any transition!
operation:
remove field -= Some(v);The resulting exchange function will consume a tok token with value v
as a parameter.
Instead of specifying v as an exact expression, you can also pattern-match
by using the let keyword.
remove field -= Some(let $pat);This will require the prior value of field to match Some($pat),
and this statement binds all the variables in $pat for use later in the transition.
Checking the value of the token
To check the value of the token without removing it,
write, inside any transition!, readonly! or property! operation:
have field >= Some(v);The resulting exchange function will accept an immutable reference
&tok (that is, it takes the token as input but does not consume it).
Instead of specifying v as an exact expression, you can also pattern-match
by using the let keyword.
have field >= Some(let $pat);This will require the prior value of field to match Some($pat),
and this statement binds all the variables in $pat for use later in the transition.
Updating a token
To update the value of an option token, first remove it, then add it,
in sequence.
remove field -= Some(let _);
add field += Some(new_v);Operations that manipulate optional tokens
You can also write versions of the above operations that operate on optional tokens.
The operations below are equivalent to the above versions whenever opt_v == Some(v),
and they are all no-ops when opt_v == None.
To create an Option<tok>:
add field += (opt_v);To consume an Option<tok>:
remove field -= (opt_v);To check the value of an &Option<tok>:
have field >= (opt_v);The value of opt_v is related to the value of
Option<tok>
as they are for initialization.
Example
tokenized_state_machine!{ State {
fields {
#[sharding(variable)]
pub token_exists: bool,
#[sharding(option)]
pub field: Option<int>,
}
#[invariant]
pub fn token_exists_correct(&self) -> bool {
self.token_exists <==> self.field is Some
}
init!{
initialize(v: int) {
init field = Option::Some(v);
init token_exists = true;
}
}
transition!{
add_token(v: int) {
require !pre.token_exists;
update token_exists = true;
add field += Some(v);
}
}
transition!{
remove_token() {
remove field -= Some(let _);
assert pre.token_exists;
update token_exists = false;
}
}
transition!{
have_token() {
have field >= Some(let _);
assert pre.token_exists;
}
}
#[inductive(initialize)]
fn initialize_inductive(post: Self, v: int) { }
#[inductive(add_token)]
fn add_token_inductive(pre: Self, post: Self, v: int) { }
#[inductive(remove_token)]
fn remove_token_inductive(pre: Self, post: Self) { }
#[inductive(have_token)]
fn have_token_inductive(pre: Self, post: Self) { }
}}
proof fn option_example() {
let tracked (Tracked(instance), Tracked(mut token_exists), Tracked(token_opt)) =
State::Instance::initialize(5);
let tracked token = token_opt.tracked_unwrap();
assert(token.value() == 5);
instance.have_token(&token_exists, &token);
assert(token_exists.value() == true);
instance.remove_token(&mut token_exists, token); // consumes token
assert(token_exists.value() == false); // updates token_exists to `false`
let tracked token = instance.add_token(19, &mut token_exists);
assert(token_exists.value() == true); // updates token_exists to `true`
assert(token.value() == 19); // new token has value 19
}
The map strategy
The map strategy can be applied to fields of type Map<K, V> for any types K and V.
fields {
#[sharding(map)]
pub field: Map<K, V>,
}Tokens.
VerusSync creates a fresh token type, tok,
named State::field where State is the name of the VerusSync system and field is the name of the field.
The token type tok implements the
UniqueKeyValueToken<V> trait.
For dealing with collections of tokens, VerusSync uses
MapToken<K, V, tok>. It also creates a type alias for this type by appending _map to the field name, e.g., State::field_map.
Relationship between global field value and the token.
Every token represents a single key-value pair (given by the .key() and .value()
functions on the UniqueKeyValueToken<V> trait).
The value of the field on the global state is the map given by the collection of key-value pairs.
Manipulation of the field
Quick Reference
In the following table, k: K, v: v, and m: Map<K, V>.
| Command | Meaning in transition | Exchange Fn Parameter |
|---|---|---|
init field = m; |
init field = m; |
Output MapToken<K, V, tok> |
remove field -= [k => v]; |
require field.dom().contains(k) && field[k] == v;update field = field.remove(k); |
Input tok |
have field >= [k => v]; |
require field.dom().contains(k) && field[k] == v; |
Input &tok |
add field += [k => v]; |
assert !field.dom().contains(k);update field = field.insert(k, v); |
Output tok |
remove field -= (m); |
require m.submap_of(field);update field = field.remove_keys(m.dom()); |
Input MapToken<K, V, tok> |
have field >= (m); |
require m.submap_of(field); |
Input &MapToken<K, V, tok> |
add field += (m); |
assert field.dom().disjoint(m.dom());update field = field.union_prefer_right(m);
|
Output MapToken<K, V, tok> |
Initializing the field
Initializing the field is done with the usual init statement (as it for all strategies).
init field = m;The instance-init function will return a token token of type
MapToken<K, V, tok>, where token.map() == m.
Adding a token
To write an operation that creates a token with key-value pair k, v,
equivalently, inserting the pair k, v into the map, write, inside any transition! operation:
add field += [k => v];This operation has an inherent safety condition that k is not in the domain of the pre-state value of the map.
The resulting token exchange function will return a token of type tok
and with key() equal to k and value() equal to v.
If you require manual proof to prove the inherent safety condition, you can add
an optional by clause:
add field += [k => v]
by {
// proof goes here
};Removing a token
To write an operation that removes a token with key-value pair k, v,
equivalently, removing the pair k, v from the map, write, inside any transition! operation:
remove field -= [k => v];The resulting exchange function will consume a tok token with key() equal to k and value() equal to v.
Instead of specifying v as an exact expression, you can also pattern-match
by using the let keyword.
remove field -= [k => let $pat];This will require the prior value of field[k] to match $pat,
and this statement binds all the variables in $pat for use later in the transition.
Checking the value of the token
To check the key and value of the token without removing it,
write, inside any transition!, readonly! or property! operation:
have field >= [k => v];The resulting exchange function will accept an immutable reference
&tok (that is, it takes the token as input but does not consume it).
Instead of specifying v as an exact expression, you can also pattern-match
by using the let keyword.
have field >= [k => let $pat];This will require the prior value of field to match $pat,
and this statement binds all the variables in $pat for use later in the transition.
Updating a token
To update the value of a map token, first remove it, then add it,
in sequence.
remove field -= [k => let _];
add field += [k => v];Operations that manipulate collections of tokens
You can also write versions of the above operations that
use a map map_toks: Map<K, Tok>,
Such token collections are managed as MapToken<K, V, tok> objects.
The operations below are equivalent to the above versions whenever m == map![k => v],
and they are all no-ops when m == map![].
To create a MapToken<K, V, tok> where tok.map() == m:
add field += (m);To consume a MapToken<K, V, tok> where tok.map() == m:
remove field -= (m);To check the value of a &MapToken<K, V, tok> where tok.map() == m:
have field >= (m);Example
TODO
The set strategy
The set strategy can be applied to fields of type Set<E> for any types E.
fields {
#[sharding(set)]
pub field: Set<E>,
}Tokens.
VerusSync creates a fresh token type, tok,
named State::field where State is the name of the VerusSync system and field is the name of the field.
The token type tok implements the
UniqueElementToken<V> trait.
For dealing with collections of tokens, VerusSync uses
SetToken<K, V, tok>. It also creates a type alias for this type by appending _set to the field name, e.g., State::field_set.
Relationship between global field value and the token.
Every token represents a single element of the set (given by the .element()
function on the UniqueElementToken<V> trait).
The value of the field on the global state is the set given by the collection of all such elements.
Manipulation of the field
Quick Reference
In the following table, e: E and s: Set<E>.
| Command | Meaning in transition | Exchange Fn Parameter |
|---|---|---|
init field = s; |
init field = s; |
Output SetToken<K, V, tok> |
remove field -= set { e }; |
require field.contains(e);update field = field.remove(e); |
Input tok |
have field >= set { e }; |
require field.contains(e); |
Input &tok |
add field += set { e }; |
assert !field.contains(e);update field = field.insert(e); |
Output tok |
remove field -= (s); |
require s.subset_of(field);update field = field.difference(s); |
Input SetToken<K, V, tok> |
have field >= (s); |
require s.subset_of(field); |
Input &SetToken<K, V, tok> |
add field += (s); |
assert field.disjoint(s);update field = field.union(s);
|
Output SetToken<K, V, tok> |
Initializing the field
Initializing the field is done with the usual init statement (as it for all strategies).
init field = s;The instance-init function will return a token token of type
SetToken<K, V, tok>, where token.set() == s.
Adding a token
To write an operation that creates a token with element e,
equivalently, inserting the element e into the set, write, inside any transition! operation:
add field += set { e };This operation has an inherent safety condition that e is not in the pre-state value of the set.
The resulting token exchange function will return a token of type tok
and with element() equal to e.
If you require manual proof to prove the inherent safety condition, you can add
an optional by clause:
add field += set { e } by {
// proof goes here
};Removing a token
To write an operation that removes a token with element e,
equivalently, removing the element e from the set, write, inside any transition! operation:
remove field -= set { e };The resulting exchange function will consume a tok token with element() equal to e.
Checking the value of the token
To check the element of the token without removing it,
write, inside any transition!, readonly! or property! operation:
have field >= set { e };The resulting exchange function will accept an immutable reference
&tok (that is, it takes the token as input but does not consume it).
Operations that manipulate collections of tokens
You can also write versions of the above operations that operate on sets of tokens
rather than singleton elements.
Such token collections are managed as SetToken<K, V, tok> objects.
The operations below are equivalent to the above versions whenever s == set![e],
and they are all no-ops when s == set![].
To create a SetToken<K, V, tok> where tok.set() == s:
add field += (s);To consume a SetToken<K, V, tok> where tok.set() == s:
remove field -= (s);To check the value of a &SetToken<K, V, tok> where tok.set() == s:
have field >= (s);Example
TODO
The multiset strategy
The multiset strategy can be applied to fields of type Multiset<E> for any types E.
fields {
#[sharding(multiset)]
pub field: Multiset<E>,
}Tokens.
VerusSync creates a fresh token type, tok,
named State::field where State is the name of the VerusSync system and field is the name of the field.
The token type tok implements the
UniqueElementToken<V> trait.
For dealing with collections of tokens, VerusSync uses
MultisetToken<K, V, tok>. It also creates a type alias for this type by appending _set to the field name, e.g., State::field_set.
Relationship between global field value and the token.
Every token represents a single element of the multiset (given by the .element()
function on the UniqueElementToken<V> trait).
The value of the field on the global state is the multiset given by the collection of all such elements.
Manipulation of the field
Quick Reference
In the following table, e: E and m: Multiset<E>.
| Command | Meaning in transition | Exchange Fn Parameter |
|---|---|---|
init field = m; |
init field = m; |
Output MultisetToken<K, V, tok> |
remove field -= { e }; |
require field.contains(e);update field = field.remove(e); |
Input tok |
have field >= { e }; |
require field.contains(e); |
Input &tok |
add field += { e }; |
update field = field.insert(e); |
Output tok |
remove field -= (m); |
require m.subset_of(field);update field = field.difference_with(m); |
Input MultisetToken<K, V, tok> |
have field >= (m); |
require m.subset_of(field); |
Input &MultisetToken<K, V, tok> |
add field += (m); |
update field = field.add(m);
|
Output MultisetToken<K, V, tok> |
Initializing the field
Initializing the field is done with the usual init statement (as it for all strategies).
init field = m;The instance-init function will return a token token of type
MultisetToken<K, V, tok>, where token.multiset() == m.
Adding a token
To write an operation that creates a token with element e,
equivalently, inserting the element e into the multiset, write, inside any transition! operation:
add field += { e };This operation has an inherent safety condition that e is not in the pre-state value of the multiset.
The resulting token exchange function will return a token of type tok
and with element() equal to e.
If you require manual proof to prove the inherent safety condition, you can add
an optional by clause:
add field += { e } by {
// proof goes here
};Removing a token
To write an operation that removes a token with element e,
equivalently, removing the element e from the multiset, write, inside any transition! operation:
remove field -= { e };The resulting exchange function will consume a tok token with element() equal to e.
Checking the value of the token
To check the element of the token without removing it,
write, inside any transition!, readonly! or property! operation:
have field >= { e };The resulting exchange function will accept an immutable reference
&tok (that is, it takes the token as input but does not consume it).
Operations that manipulate collections of tokens
You can also write versions of the above operations that operate on variable-sized collections of tokens
rather than singleton elements.
Such token collections are managed as MultisetToken<K, V, tok> objects.
The operations below are equivalent to the above versions whenever m == multiset![e],
and they are all no-ops when m == multiset![].
To create a MultisetToken<K, V, tok> where tok.multiset() == m:
add field += (m);To consume a MultisetToken<K, V, tok> where tok.multiset() == m:
remove field -= (m);To check the value of a &MultisetToken<K, V, tok> where tok.multiset() == m:
have field >= (m);Example
TODO
The bool strategy
The bool strategy can be applied to fields of type bool.
fields {
#[sharding(bool)]
pub field: bool,
}Tokens.
VerusSync creates a fresh token type, tok,
named State::field where State is the name of the VerusSync system and field is the name of the field.
The token type tok implements the
UniqueSimpleToken trait.
Relationship between global field value and the token.
When field is false, this corresponds to no token existing, while
when field is true, this corresponds to a token existing.
The token doesn’t contain any additional data.
Having multiple such tokens at the same time is an impossible state.
Manipulation of the field
Quick Reference
In the following table, b: bool.
| Command | Meaning in transition | Exchange Fn Parameter |
|---|---|---|
init field = b; |
init field = b; |
Output Option<tok> |
remove field -= true; |
require field == true;update field = false; |
Input tok |
have field >= true; |
require field == true; |
Input &tok |
add field += true; |
assert field == false;update field = true; |
Output tok |
remove field -= (b); |
require (b ==> field);
update field = field && !b; |
Input Option<tok> |
have field >= (b); |
require (b ==> field); |
Input &Option<tok> |
add field += (b); |
assert !(field && b);
update field = field || b; |
Output Option<tok> |
Initializing the field
Initializing the field is done with the usual init statement (as it for all strategies).
init field = b;The instance-init function will return a token of type Option<tok>,
related as follows:
value of b: bool |
value of optional token Option<tok> |
|---|---|
false |
None |
true |
Some(tok) where tok.value() == v |
Adding a token
To write an operation that creates a token,
equivalently,
updating the field’s value from false to true, write, inside any transition!
operation:
add field += true;This operation has an inherent safety condition that the prior value of field is false.
The resulting token exchange function will return a token of type tok.
Removing a token
To write an operation that removes a token,
equivalently,
updating the field’s value from true to false, write, inside any transition!
operation:
remove field -= true;The resulting exchange function will consume a tok token
as a parameter.
Checking the value of the token
To check the value of the token without removing it,
write, inside any transition!, readonly! or property! operation:
have field >= true;The resulting exchange function will accept an immutable reference
&tok (that is, it takes the token as input but does not consume it).
Operations that manipulate optional tokens
You can also write versions of the above operations that operate on optional tokens.
The operations below are equivalent to the above versions whenever b == true,
and they are all no-ops when b == false.
To create an Option<tok>:
add field += (b);To consume an Option<tok>:
remove field -= (b);To check the value of an &Option<tok>:
have field >= (b);The value of b is related to the value of
Option<tok>
as they are for initialization.
Example
TODO
The count strategy
The count strategy can be applied to fields of type nat.
fields {
#[sharding(count)]
pub field: nat,
}Tokens.
VerusSync creates a fresh token type, tok,
named State::field where State is the name of the VerusSync system and field is the name of the field.
The token type tok implements the
CountToken trait.
Each token has a count() value, and these tokens
“fungible” in the sense that they can be combined and split, numbers
combining additively.
Relationship between global field value and the token.
The global value of the field is the sum of the counts of all the tokens.
Manipulation of the field
Quick Reference
In the following table, n: nat.
| Command | Meaning in transition | Exchange Fn Parameter |
|---|---|---|
init field = n; |
init field = n; |
Output tok |
remove field -= (n); |
require field >= n;update field = field - n; |
Input tok |
have field >= n; |
require field >= n; |
Input &tok |
add field += n; |
update field = field + n; |
Output tok |
Initializing the field
Initializing the field is done with the usual init statement (as it for all strategies).
init field = n;The instance-init function will return a token of type tok
with count() equal to n.
Adding a token (increasing the count)
To write an operation that creates a token, equivalently, adding to the total count, write,
add field += (n);The resulting token exchange function will return a token of type tok
with count() equal to n.
Removing a token
To write an operation that removes a token,
equivalently, decreasing the total count,
updating the field’s value from true to false, write, inside any transition!
operation:
remove field -= (n);The resulting exchange function will consume a tok token
with count() equal to n
as a parameter.
Checking the value of the token
To check the value of the token without removing it,
write, inside any transition!, readonly! or property! operation:
have field >= (n);The resulting exchange function will accept an immutable reference
&tok (that is, it takes the token as input but does not consume it).
Example
TODO
The persistent_option strategy
The persistent_option strategy can be applied to fields of type Option<V> for any type V.
fields {
#[sharding(persistent_option)]
pub field: Option<V>,
}Tokens.
VerusSync creates a fresh token type, tok,
named State::field where State is the name of the VerusSync system and field is the name of the field.
The token type tok implements the
ValueToken<V> trait. It also implements Copy.
Relationship between global field value and the token.
When field is None, this corresponds to no token existing, while
when field is Some(v), this corresponds to a token of value v existing.
Since the token is Copy, there can be any number of such tokens. Once set to a particular
Some(_) value, it can never be set to a different one; i.e., it can only be set
None -> Some.
Manipulation of the field
Quick Reference
In the following table, v: V and v_opt: Option<V>.
| Command | Meaning in transition | Exchange Fn Parameter |
|---|---|---|
init field = v_opt; |
init field = v_opt; |
Output Option<tok> |
have field >= Some(v); |
require field == Some(v); |
Input &tok |
add field (union)= Some(v); |
assert field == None || field == Some(v);update field = Some(v); |
Output tok |
have field >= (v_opt); |
require v_opt == None || field == v_opt; |
Input &Option<tok> |
add field (union)= (v_opt); |
assert field == None || v_opt == None || field == v_opt;
update field = if v_opt == None { field }
else { v_opt }; |
Output Option<tok> |
Initializing the field
Initializing the field is done with the usual init statement (as it for all strategies).
init field = opt_v;The instance-init function will return a token of type Option<tok>,
related as follows:
value of opt_v: Option<V> |
value of optional token Option<tok> |
|---|---|
None |
None |
Some(v) |
Some(tok) where tok.value() == v |
Adding a token
To write an operation that creates a token with value v,
write, inside any transition! operation:
add field (union)= Some(v);This operation has an inherent safety condition that the prior value of field is either None
or is already Some(v).
The resulting token exchange function will return a token of type tok
and with value v.
In other words, you can create a token only if the existing value is None (no tokens have been created yet)
or already equal to Some(v) (all existing tokens agree with the new token on the value).
If you require manual proof to prove the inherent safety condition, you can add
an optional by clause:
add field (union)= Some(v)
by {
// proof goes here
};Checking the value of the token
To check the value of a token,
write, inside any transition!, readonly! or property! operation:
have field >= Some(v);The resulting exchange function will accept an immutable reference
&tok (that is, it takes the token as input but does not consume it).
Instead of specifying v as an exact expression, you can also pattern-match
by using the let keyword.
have field >= Some(let $pat);This will require the prior value of field to match Some($pat),
and this statement binds all the variables in $pat for use later in the transition.
Operations that manipulate optional tokens
You can also write versions of the above operations that operate on an optional token
opt_tok: Option<Tok>.
The operations below are equivalent to the above versions whenever opt_tok == Some(v),
and they are all no-ops when opt_tok == None.
To create an opt_tok: Option<tok>:
add field (union)= (opt_tok);To check the value of an &Option<tok>:
have field >= (opt_tok);The value of opt_tok is related to the value of
Option<tok>
as they are for initialization.
Example
TODO
The persistent_map strategy
The persistent_map strategy can be applied to fields of type Map<K, V> for any types K and V.
fields {
#[sharding(persistent_map)]
pub field: Map<K, V>,
}Tokens.
VerusSync creates a fresh token type, tok,
named State::field where State is the name of the VerusSync system and field is the name of the field.
The token type tok implements the
KeyValueToken<V> trait.
For dealing with collections of tokens, VerusSync uses
MapToken<K, V, tok>. It also creates a type alias for this type by appending _map to the field name, e.g., State::field_map.
Relationship between global field value and the token.
Every token represents a single key-value pair (given by the .key() and .value()
functions on the KeyValueToken<V> trait).
The value of the field on the global state is the map given by the collection of key-value pairs.
Since the tokens are Copy, there can be any number of such tokens for any given key.
Of course, all such tokens for the same key will agree on the value as well. Once a key is set to a given value, this cannot be changed or removed.
Manipulation of the field
Quick Reference
In the following table, k: K, v: v, and m: Map<K, V>.
| Command | Meaning in transition | Exchange Fn Parameter |
|---|---|---|
init field = m; |
init field = m; |
Output MapToken<K, V, tok> |
have field >= [k => v]; |
require field.dom().contains(k) && field[k] == v; |
Input &tok |
add field (union)= [k => v]; |
assert field.dom().contains(k) ==> field[k] == v;update field = field.insert(k, v); |
Output tok |
have field >= (m); |
require m.submap_of(field); |
Input &MapToken<K, V, tok> |
add field (union)= (m); |
assert field.agrees(m);update field = field.union_prefer_right(m);
|
Output MapToken<K, V, tok> |
Initializing the field
Initializing the field is done with the usual init statement (as it for all strategies).
init field = m;The instance-init function will return a token token of type
MapToken<K, V, tok>, where token.map() == m.
Adding a token
To write an operation that creates a token with key-value pair k, v,
write, inside any transition! operation:
add field (union)= [k => v];This operation has an inherent safety condition that, if k is in the domain of the pre-state value of the map, then it has the same value v.
The resulting token exchange function will return a token of type tok
and with key() equal to k and value() equal to v.
If you require manual proof to prove the inherent safety condition, you can add
an optional by clause:
add field (union)= [k => v]
by {
// proof goes here
};Checking the value of the token
To check the key and value of the token,
write, inside any transition!, readonly! or property! operation:
have field >= [k => v];The resulting exchange function will accept an immutable reference
&tok (that is, it takes the token as input but does not consume it).
Instead of specifying v as an exact expression, you can also pattern-match
by using the let keyword.
have field >= [k => let $pat];This will require the prior value of field to match $pat,
and this statement binds all the variables in $pat for use later in the transition.
Operations that manipulate collections of tokens
You can also write versions of the above operations that operate on variable-sized collections of tokens
rather than singleton key-value pairs.
Such token collections are managed as MapToken<K, V, tok> objects.
The operations below are equivalent to the above versions whenever m == map![k => v],
and they are all no-ops when m == map![].
To create a MapToken<K, V, tok> where tok.map() == m:
add field (union)= (m);To check the value of a &MapToken<K, V, tok> where tok.map() == m:
have field >= (m);Example
TODO
The persistent_bool strategy
The persistent_bool strategy can be applied to fields of type bool.
fields {
#[sharding(bool)]
pub field: bool,
}Tokens.
VerusSync creates a fresh token type, tok,
named State::field where State is the name of the VerusSync system and field is the name of the field.
The token type tok implements the
SimpleToken<V> trait.
Relationship between global field value and the token.
When field is false, this corresponds to no token existing, while
when field is true, this corresponds to at least one token existing.
The token doesn’t contain any additional data.
Having multiple such tokens at the same time is an impossible state.
Since the tokens are Copy, there can be any number of such tokens for any given key.
Manipulation of the field
Quick Reference
In the following table, b: bool.
| Command | Meaning in transition | Exchange Fn Parameter |
|---|---|---|
init field = b; |
init field = b; |
Output Option<tok> |
have field >= true; |
require field == true; |
Input &tok |
add field (union)= true; |
update field = true; |
Output tok |
have field >= (b); |
require b ==> field; |
Input &Option<tok> |
add field (union)= (b); |
update field = field || b; |
Output Option<tok> |
Initializing the field
Initializing the field is done with the usual init statement (as it for all strategies).
init field = b;The instance-init function will return a token of type Option<tok>,
related as follows:
value of b: bool |
value of optional token Option<tok> |
|---|---|
false |
None |
true |
Some(tok) |
Adding a token
To write an operation that creates a token,
write, inside any transition! operation:
add field (union)= true;The resulting token exchange function will return a token of type tok
and with value v.
In other words, you can create a token at any time, regardless of the current value of the field. The only requirement is that (as always) the invariants of the system must be preserved.
Observing that the token exists
To observe that the token exists,
write, inside any transition!, readonly! or property! operation:
have field >= true;The resulting exchange function will accept an immutable reference
&tok (that is, it takes the token as input but does not consume it).
Operations that manipulate optional tokens
You can also write versions of the above operations that operate on optional tokens.
The operations below are equivalent to the above versions whenever opt_v == Some(v),
and they are all no-ops when opt_v == None.
To create an Option<tok>:
add field (union)= (b);To observe the token &Option<tok>:
have field >= (b);The value of b is related to the value of
Option<tok>
as they are for initialization.
Example
TODO
not_tokenized
The not_tokenized strategy can be applied to fields of any type V.
fields {
#[sharding(not_tokenized)]
pub field: V,
}This results in no token types associated to the field field.
It is often useful as a convenient alternative when you would otherwise need an existential variable in the VerusSync invariant.
Manipulation of the field
Initializing the field
Initializing the field is done with the usual init statement (as it for all strategies).
init field = v;Of course, the instance-init function does not emit any tokens for this instruction.
Reading the field
Reading the field can be done by writing pre.field. Notably, this causes the resulting
operation to be non-deterministic in its input arguments. Therefore, pre.field can
only be accessed in a birds_eye context.
Updating the field
The field can always be updated with an update statement in any transition! operation.
update field = v;This does not result in any token inputs or token outputs, and it has no effect on the
signature of the token operation. The update instruction may be required in order to
preserve the system invariant.
Example
TODO
The storage_option strategy
The storage_option strategy can be applied to fields of type Option<Tok>
for any type Tok.
fields {
#[sharding(storage_option)]
pub field: Option<Tok>,
}Tokens.
Usually Tok is itself some “token” type intended for tracked
contexts—e.g., the token created by a different VerusSync system
(or even the same VerusSync system, as recursive types are permitted),
a PointsTo,
or a datatype/tuple combining multiple of these.
VerusSync does not create any additional tokens for the field.
Relationship between global field value and the token.
When a field is declared storage_option, the VerusSync gains the ability to “store”
tokens of the given type Tok. A field value of None means nothing is stored;
a field value of Some(tok) means the token tok is stored.
Manipulation of the field
Quick Reference
In the following table, tok: Tok, and opt_token: Option<Tok>.
| Command | Meaning in transition | Exchange Fn Parameter |
|---|---|---|
init field = opt_tok; |
init field = opt_tok; |
Input Option<Tok> |
deposit field += Some(tok); |
assert field == None;update field = Some(tok); |
Input Tok |
guard field >= Some(tok); |
assert field == Some(tok); |
Output &Tok |
withdraw field -= Some(tok); |
assert field == Some(tok);update field = None; |
Output Tok |
deposit field += opt_tok; |
assert field == None || opt_tok == None;update field = opt_tok; |
Input Option<Tok> |
guard field >= opt_tok; |
assert opt_tok.is_some() ==> field == opt_tok; |
Output &Option<Tok> |
withdraw field -= opt_tok; |
assert opt_tok.is_some() ==> field == opt_tok;update field = if opt_tok == None { field } else { None }; |
Output Option<Tok> |
Initializing the field
Initializing the field is done with the usual init statement (as it for all strategies).
init field = opt_tok;The instance-init function will take as input a token of type Option<Tok>,
equal to the value of opt_tok.
That is, if opt_tok is None, then the initial state has nothing “stored” and passing None to the constructor is trivial;
if opt_tok is Some(tok), then the initial state has tok “stored” and it must be supplied via the input argument for the constructor.
Performing a deposit
To deposit a token tok: Tok, use the deposit statement in any transition! operation:
deposit field += Some(tok);
This sets the field value to Some(tok). The resulting token operation then takes a token equal to tok as input.
The deposit instruction has an inherent safety condition that field is None in the pre-state. (Note: this is not strictly necessary, and the restriction may be removed later.)
If you require manual proof to prove the inherent safety condition, you can add
an optional by clause:
deposit field += Some(v)
by {
// proof goes here
};Performing a withdraw
To withdraw a token tok: Tok, use the withdraw statement in any transition! operation:
withdraw field -= Some(tok);
This sets the field value to None. The resulting token operation then returns a token
equal to tok in its output.
The withdraw instruction has an inherent safety condition that field is Some(tok) in the pre-state.
Manual proofs. If you require manual proof to prove the inherent safety condition, you can add
an optional by clause:
withdraw field -= Some(tok)
by {
// proof goes here
};Using patterns. Instead of specifying tok as an exact expression, you can also pattern-match
by using the let keyword.
withdraw field -= Some(let $pat);
In this case, the inherent safety condition is that the field value is Some and that
the inner value matches $pat. In this case, note that the value matched on $pat is
not deterministic in the input arguments of the token operation. Therefore,
VerusSync considers any variables bound in $pat to implicitly be birds_eye
binders. Specifically, the pattern-matching variant is equivalent to:
birds_eye let stored_value = pre.field.unwrap();
withdraw field -= Some(stored_value);
birds_eye let $pat = stored_value;
Performing a guard (obtaining a shared reference to the stored object)
To guard a token tok: Tok, use the guard statement in any property! operation:
guard field >= Some(tok);
The resulting token operation then returns a shared reference to the token
equal to tok in its output. The shared reference has a lifetime bounded by the lifetimes
of the input references.
The guard instruction has an inherent safety condition that field is Some(tok) in the pre-state.
Manual proofs. If you require manual proof to prove the inherent safety condition, you can add
an optional by clause:
guard field >= Some(tok)
by {
// proof goes here
};Operations that manipulate optional tokens
You can also write versions of the above operations that operate on an optional token
opt_tok: Option<Tok>.
The operations below are equivalent to the above versions whenever opt_tok == Some(tok),
and they are all no-ops when opt_tok == None.
To deposit opt_tok: Option<Tok>:
deposit field += (opt_tok);To withdraw opt_tok: Option<Tok>:
remove field -= (opt_tok);To obtain opt_tok: &Option<Tok>:
guard field >= (opt_v);Example
TODO
The storage_map strategy
The storage_map strategy can be applied to fields of type Map<K, Tok>
for any types K and Tok.
fields {
#[sharding(storage_map)]
pub field: Map<K, Tok>,
}Tokens.
Usually Tok is itself some “token” type intended for tracked
contexts—e.g., the token created by a different VerusSync system
(or even the same VerusSync system, as recursive types are permitted),
a PointsTo,
or a datatype/tuple combining multiple of these.
VerusSync does not create any additional tokens for the field.
Relationship between global field value and the token.
When a field is declared storage_map, the VerusSync gains the ability to “store”
tokens of the given type Tok. Multiple such tokens can be stored,
and they are indexed by keys of type K.
For example, if the field has value [1 => tok1, 4 => tok2], then that means tok1 and tok2 are stored.
Manipulation of the field
Quick Reference
In the following table, k: K, tok: Tok, and map_toks: Map<K, Tok>.
| Command | Meaning in transition | Exchange Fn Parameter |
|---|---|---|
init field = map_toks; |
init field = map_toks; |
Input Map<K, Tok> |
deposit field += [ k => tok ]; |
assert !field.dom().contains(k);update field = field.insert(k, tok); |
Input Tok |
guard field >= [ k => tok ]; |
assert field.dom().contains(k) && field[k] == tok; |
Output &Tok |
withdraw field -= [ k => tok ]; |
assert field.dom().contains(k) && field[k] == tok;update field = field.remove(k); |
Output Tok |
deposit field += map_toks; |
assert field.dom().disjoint(map_toks.dom());update field = field.union_prefer_right(map_toks);
|
Input Map<K, Tok> |
guard field >= map_toks; |
assert map_toks.submap_of(field); |
Output &Map<K, Tok> |
withdraw field -= map_toks; |
assert map_toks.submap_of(field);update field = field.remove_keys(map_toks.dom()); |
Output Map<K, Tok> |
Initializing the field
Initializing the field is done with the usual init statement (as it for all strategies).
init field = map_toks;The instance-init function will take as input a token of type Map<K, Tok>,
equal to the value of map_toks.
Performing a deposit
To deposit a token tok: Tok, use the deposit statement in any transition! operation:
deposit field += [ k => tok ];
This sets the map value at key k to tok. The resulting token operation then takes a token equal to tok as input.
The deposit instruction has an inherent safety condition that key is not already present in the pre-state. (Note: this is not strictly necessary, and the restriction may be removed later.)
If you require manual proof to prove the inherent safety condition, you can add
an optional by clause:
deposit field += [ k => tok ] by {
// proof goes here
};Performing a withdraw
To withdraw a token tok: Tok, use the withdraw statement in any transition! operation:
withdraw field -= [ k => tok ];
This sets the field value to None. The resulting token operation then returns a token
equal to tok in its output.
The withdraw instruction has an inherent safety condition that field contains the key-value pair k, tok in the pre-state.
Manual proofs. If you require manual proof to prove the inherent safety condition, you can add
an optional by clause:
withdraw field -= [ k => tok ] by {
// proof goes here
};Using patterns. Instead of specifying tok as an exact expression, you can also pattern-match
by using the let keyword.
withdraw field -= [ k => let $pat ];
In this case, the inherent safety condition is that the field map contains the key k and that
the corresponding value matches $pat. In this case, note that the value matched on $pat is
not deterministic in the input arguments of the token operation. Therefore,
VerusSync considers any variables bound in $pat to implicitly be birds_eye
binders. Specifically, the pattern-matching variant is equivalent to:
birds_eye let stored_value = pre.field[k];
withdraw field -= [ k => stored_value ];
birds_eye let $pat = stored_value;
Performing a guard (obtaining a shared reference to the stored object)
To guard a token tok: Tok, use the guard statement in any property! operation:
guard field >= [ k => tok ];
The resulting token operation then returns a shared reference to the token
equal to tok in its output. The shared reference has a lifetime bounded by the lifetimes
of the input references.
The guard instruction has an inherent safety condition that field contains the key-value pair k, tok in the pre-state.
Manual proofs. If you require manual proof to prove the inherent safety condition, you can add
an optional by clause:
guard field >= [ k => tok ];
by {
// proof goes here
};Operations that manipulate collections of tokens
You can also write versions of the above operations that
use a map map_toks: Map<K, Tok>,
instead of an individual key-value pair (typically you’ll need to pass map_toks in as an argument to your transition).
The operations below are equivalent to the above versions whenever map_toks == [ k => tok ],
and they are all no-ops when map_toks == map![].
To deposit map_toks: Map<K, Tok>:
deposit field += (map_toks);To withdraw map_toks: Map<K, Tok>:
remove field -= (map_toks);To obtain map_toks: &Map<K, Tok>:
guard field >= (map_toks);Example
TODO
Properties
The property! operation is not actually a transition. Instead, it allows you to export
useful facts from the state-machine view of the world to thread-local reasoning in your
implementation.
For example, suppose your state machine has:
fields {
#[sharding(bool)]
pub waiting: bool,
#[sharding(variable)]
pub num_remaining: nat,
...
}where num_remaining corresponds to an atomic U32 counting the number of
threads that still need to perform an operation. You could represent this by
maintaining a state-machine level invariant that self.waiting ==> self.num_remaining > 0. However, that fact is not available in your code by
default. Hence, if your code needs to prove, say, that when it decreases the
atomic U32, the value does not wrap around, you can establish this via a
property:
property! {
waiting_means_positive() {
assert(self.waiting ==> self.num_remaining > 0);
}
}Verus will check that the invariant establishes this property, and then it will make
waiting_means_positive available to the code as a lemma that can be invoked on the
state-machine’s Instance.
You can also use a property! to establish a proof-by-contradiction. Continuing the example
above, suppose you also maintain an invariant that num_remaining < 10. In your implementation,
perhaps your code contains a function that receives a token tok representing
num_remaining but doesn’t know how large the contained value might be. To prove that the value
isn’t too large, you can use a property like this:
property! {
in_bounds() {
have num_remaining >= (10);
assert(false);
}
}Again, Verus will check that the invariant establishes this property, and then
it will make in_bounds available to the code as a lemma that can be invoked
on the state-machine’s Instance. Invoking that lemma with a shared reference
to tok will allow the code to conclude that the value in tok must be less
than 10.
Finally, when working with storage strategies (e.g.,
storage_option or
storage_map), to obtain a shared permission to the
stored value, you can use the guard operation inside a property. For
instance, if your state machine has:
fields {
#[sharding(bool)]
pub deposited: bool,
#[sharding(storage_option)]
pub perm: Option<Perm>,
...
}then you can write a property like this:
property! {
get_perm_ref(x: Perm) {
have deposited >= (true);
guard perm >= (Some(x));
}
}Verus will check that your invariant implies that perm is Some (e.g.,
perhaps your invariant says self.deposited ==> self.perm.is_some()).
VerusSync will make get_perm_ref available to the code as a lemma that can be
invoked on the state-machine’s Instance. Invoking that lemma with a shared
reference to a token for deposited and the ghost value of perm will
produce a shared reference to the value in perm.
Operations
The birds_eye command
The birds_eye keyword can be used to allow unrestricted reads of the pre variable
without impacting the tokens that are input or output in the operation.
Specifically, let statements in transitions may be prefixed with the birds_eye annotation.
birds_eye let $var_name = $expr
The expression on the right-hand side may access pre.field for any field.
A birds_eye let can be used in any transition!, readonly!, or property! operation.
Though birds_eye allows accessing all fields, it is particularly useful for fields using
the not_tokenized strategy or storage-based strategies.
Impact on determinism
Ordinarily, VerusSync operations are deterministic in the input arguments and input tokens,
a property enforced by various strategy-specific restrictions on how fields may be manipulated.
However, when birds_eye is used, operations may become nondeterminstic.
Restrictions
There are two main restrictions:
-
No preconditions can depend on a
birds_eyevariable. This means thatrequire,remove,have, anddepositstatements cannot depend on abirds_eyevalue. Since this nondeterministic information is not available at the beginning of the token operation, there would be no way to create a well-formed precondition. -
No
guardoperation can depend on abirds_eyevariable. This is crucial for soundness; the value being guarded must be deterministic as otherwise, the output token&Tokmight become invalid before its lifetime expires.
These restrictions are currently implemented by a coarse-grained dependency analysis determined primarily by the order of statements, rather than the actual uses of variables. Dependency analysis may be made more precise in the future.
Impact on resulting ghost token operation
The presencne of a birds_eye let-statement does not impact the tokens that are input
or output. It does, however, create extra (ghost) out-parameters for the fields that
are referenced inside birds_eye. This allows the operation’s postconditions to
refer to these nondeterministic values.
Example
TODO
Formalism of Tokenization by monoids (TODO)
Here, we provide justification for the concurrent state machine features in terms of a (pen-and-paper) monoid formalism.
Let the state machine have state S = { f1: T1, f2: T2, ... } with an invariant Inv : S -> bool.
We define a monoid M:
enum M {
Unit,
State(g1: S1, g2: S2, ...),
Fail,
}
Each Si is a partial monoid defined in terms of Ti and its respective sharding strategy.
We let Unit, of course, be the unit, and we define x · Fail = Fail for all x. The composition of two State elements is defined pairwise, and if any of the compositions fails due to partiality, we go to the Fail state.
The sharding strategies are as follows, given in terms of a type T:
- Strategy
variable: We letSbeOption<T>withNoneas the unit, and the compositionSome(...) · Some(...)to be undefined. - Strategy
constant: We letSbeOption<T>withNoneas the unit, and the compositionSome(x) · Some(y) = if x == y { Some(x) } else { undefined }.
For each strategy we have some map W : S -> T. (In all cases, the map is either the identity or Some(_).) Now, define a predicate P : M -> bool:
P(Unit) = false
P(Fail) = false
P(State(g1, g2, ...)) = ∃ f1, f2, ... Inv(S(f1, f2, ...)) && Wi(fi) = gi
Now let V : M -> bool be given by:
V(x) = ∃ z , P(x · z)
The predicate V makes M a partial commutative monoid. From this, we can construct propositions (γ, m) where γ is a location and m : M under the standard rules, e.g., (γ, m1) * (γ, m2) <==> (γ, m1 · m2) and so on.
Now, the concurrent state machine framework produces a variety of tokens.
- The
Instancetoken (γ, c1, …, ck) contains all the data for the fields ofconstantsharding strategy. It represents the proposition(γ, State(...))with fieldsgi = Some(ci)and all other fields unital. Note that this proposition is freely duplicable (becauseSome(ci) · Some(ci) = Some(ci)). - For (non-constant) field
f, we create separate tokens for that field. Each token represents the same proposition as theInstance(which, again, is freely duplicable) and some proposition specific to the field, described below:- For a field
fiofvariablestrategy, we have a token(instance, fi)which represents the proposition(γ, State(...))with fieldgi = Some(fi)(and all other fields unital).
- For a field