Strategy Reference
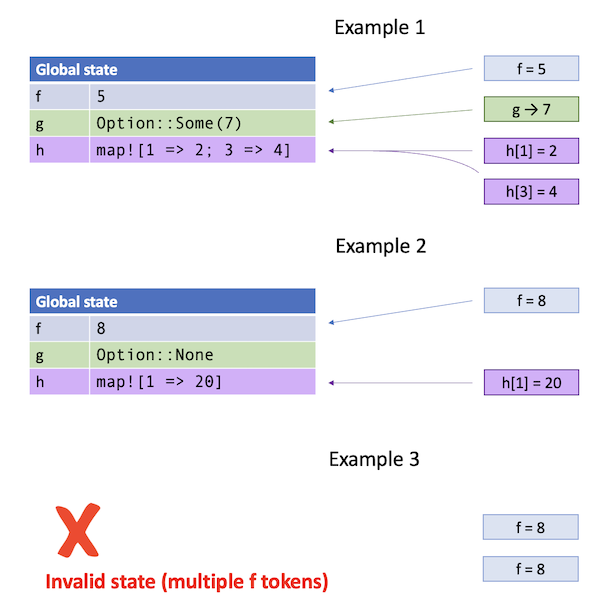
In a tokenized state machine, Verus produces a set of token types such that any state of the system represents some collection of objects of those types. This tokenization process is determined by a strategy declared on each field of the state definition. Specifically, for each field, Verus (potentially) generates a token type for the field depending on the declared strategy, with the strategy determining some relationship between the state’s field value and a collection of such tokens. The entire state, consisting of all fields, then corresponds to a collection of objects out of all the defined token types.
-
For example, consider a field
fof typeTwith strategyvariable. In this case, the token type (namedf) has a valueTon it, and we require the collection to always have exactly one such token, giving, of course, the value off. -
On the other hand, consider a field
gof typeMap<K, V>with strategymap. In this case, the token types have pairs(k, v). The collection can have any number of tokens, although they have to all have distinct keys, and the pairs all together form a map which gives the value of fieldg. -
Or consider a field
hof typeOption<V>with strategyoption. In this case, the token type has a valuev: V, and the collection must contain either no tokens for this type (yieldingOption::None), or exactly one (yieldingOption::Some(v)).
Each transition of the system can be viewed both as a transition relation in the same sense as in an orindary transition, but also as an “exchange” of tokens, where a sub-collection of tokens is taken in (consumed) and exchanged for a new sub-collection. All of the rules we discuss below are meant to ensure that each exchange performed on a valid collection will result in another valid collection and that the corresponding global system states transition according to the relation.
The Instance token and the constant strategy
Every tokenized state machine generates a special Instance token type.
Besides serving as a convenient object with which to serve the exchange function API,
the Instance also serves as “unique identifier” for a given instantiation of the protocol.
All other token types have an instance: Instance field, and in any exchange, all
of these instance markers are required to match.
The Instance type implements Clone, so it can be freely shared by all the clients
that need to manipulate some aspect of the protocol.
The Instance type also contains all fields declared with the constant strategy,
accessed as instance.field_name(). Fields with the constant strategy cannot be updated
after the protocol has been initialized, so this information will never be inconsistent.
Furthermore, constant fields do not not generate their own constant types.
The variable strategy
If a field f has strategy variable, then Verus generates a token type f, with values
given by token![$instance => f => $value].
Verus enforces that there is always exactly one token of the type f.
(Technical note: the reader might wonder what happens if the user attempts to drop the token.
This is allowed because dropped tokens are still considered to “exist” in the perspective of the abstract ghost program. Dropping a token only means that it is made inaccessible.)
The value of a variable field is manipulated using the ordinary update command, as in
ordinary transition definitions. The old value can be accessed as usual with pre.f.
If f is updated by a transition, then the corresponding exchange function takes an f
taken as an &mut argument. If f is read (via pre.f) but never updated, then it is
read as an & argument.
If the field is neither read nor written by the transition, then it is not taken as
an argument.
The “collection-style” strategies with remove/have/add
(TODO not all of these exist yet)
A large number of tokenization strategies are specified in what we call collection-style
or monoid-style. Specifically, this includes
option, map, multiset, set, count, and bool,
as well as their “persistent” verions
persistent_option, persistent_map, persistent_set, persistent_count, and persistent_bool.
Basic Collection Strategies
| Strategy | Type | Token value | Requirements / relationship to field value |
|---|---|---|---|
| option | Option<V> | token![$instance => f => $v] | No token for None, one token for Some(v). |
| map | Map<K, V> | token![$instance => f => $k => $v] | At most one token for any given value of k. |
| multiset | Multiset<V> | token![$instance => f => $v] | No restrictions. |
| set | Set<V> | token![$instance => f => $v] | At most one token for any given value of v. |
| count | nat | token![$instance => f => $n] | Any number of tokens; the sum of all tokens gives the field value. |
| bool | bool | token![$instance => f => true] | Token either exists (for true) or doesn’t exist (for false). |
(In the table, v has type V, k has type K, n has type nat, and b has type bool.)
Initially, some of these might seem odd—why, for example, does bool have a true token, and no false token?
However, if the user wants a false token, they can just use the variable strategy. Instead, bool, here, is meant to
represent the case where we want a token that either exists, or doesn’t, with no other information, and the natural
representation of such a thing is a bool. (Actually, bool is just isomorphic to Option<()>.)
Describing transitions for these collection types is somewhat more involved. Note that a user cannot in general
establish the exact value of one of these fields simply by providing some tokens for the field, since it’s always possible
that there are other tokens elsewhere. As such, the values of these fields are not manipulated through update but through
three commands called remove, have, and add.
To describe these, we will first establish a notion of composition on the field types.
Specifically, we define the composition a · b by the idea that if a and b each represent some collection
of tokens, then a · b should represent the union of those two collections.
Of course, this may not always be well defined: as we have discussed, not all possible collections of tokens
are valid collections for the given strategy. Thus, we let a ## b indicate that the composition is well-defined.
(Note: these operators are for documentation purposes only; currently, they are not operators that can be used in Verus code.)
| Strategy | a ## b | a · b |
|---|---|---|
| option | a === None || b === None | if a == None { b } else { a } |
| map | a.dom().disjoint(b.dom()) | a.union_prefer_right(b) |
| multiset | true | a.add(b) |
| set | a.disjoint(b) | a.union(b) |
| count | true | a + b |
| bool | !(a && b) | a || b |
Note that despite any apparent asymmetries, a · b is always commutative whenever a ## b, and these definitions
are all consistent with the union of token collections, given by the relationships in the above table.
Now, write a >= b if there exists some value c such that a · c = b.
Note that c is always unique when it exists. (This property is called cancellativity,
and it is not in general true for a monoid; however, it is true for all the ones we consider here.)
When a >= b, let a - b denote that unique value.
Now, with these operators defined, we can give a general meaning for the three transition commands,
remove, have, and add, in terms of require, update, and assert.
| Command | Meaning as transition on state | Meaning for exchange function |
|---|---|---|
remove f -= (x); | require f >= x;update f = f - x; | Input argument, consumed |
have f >= (x); | require f >= x; | Input argument of type &_ |
add f += (x); | assert f ## x;update f = f · x; | Output argument |
Furthermore, for a given field, the commands always go in the order remove before have before add.
There could be multiple, or none, of each one.
The reason is that ordering would not impact the definition of the exchange function; furthermore,
this particular ordering gives the strongest possible relation definition, so it the easiest to work with.
For example, a remove followed by a have will capture the fact the two values used as arguments
must be disjoint by ##.
Unfortunately, the type of the input or output argument is, in general, somewhat complicated,
since it needs to correspond to the value x in the above table, which takes on the same type as the
field.
For example, suppose f and x take on values of type Map<K, V> with the map strategy.
In that case, the token type (named f) represents only a single (key, value) pair of the map,
and the tracked objects passed into or out of the exchange function would need to be
maps of tokens. (TODO link to documentation about using tracked maps)
The same is true of option, set, and multiset.
In the common case, transitions are defined so that arguments in or out are just single tokens
of the token type f, in the form given in the above table.
(The primary exceptions are output arguments of the init routines
or large, bulk transitions that operate on a lot of state.)
The remove, have, and add commands all allows a syntactic shorthand for “singleton” elements:
add f += Some(x)is foroptionadd f += [k => v]is formapsingletonsadd f += {x}is formultisetandsetsingletons
Of course, this applies to remove and have as well.
The general form is add f += (x) as above, with x taking the same type as field f.
(The parentheses are necessary.)
The general form works for all the collection strategies.
Note that there is no “special” form for either count, since the general form
is perfectly suitable for those situations.
Also note that the special forms generate simpler proof obligations, and thus are easier for the SMT solver to handle.
We supply, here, a reference table for all the different possible commands for each strategy:
| Type | Command | Meaning in transition | Exchange Fn Parameter |
|---|---|---|---|
Option<V> | remove f -= Some(v); | require f === Some(v);update f = None; | Input f |
Option<V> | have f >= Some(v); | require f === Some(v); | Input &f |
Option<V> | add f += Some(v); | assert f === None;update f = Some(v); | Output f |
Option<V> | remove f -= (x); | require x === None || f === x;update f = if x === None { f } else { None }; | Input Option<f> |
Option<V> | have f >= (x); | require x === None || f === x; | Input &Option<f> |
Option<V> | add f += (x); | assert f === None || x === None;update f = if x === None { f } else { x }; | Output Option<f> |
Map<K, V> | remove f -= [k => v]; | require f.contains(k) && f.index(k) === v;update f = f.remove(k); | Input f |
Map<K, V> | have f >= [k => v]; | require f.contains(k) && f.index(k) === v; | Input &f |
Map<K, V> | add f += [k => v]; | assert !f.contains(k);update f = f.insert(k, v); | Output f |
Map<K, V> | remove f -= (x); | require x.le(f);update f = f.remove_keys(x.dom()); | Input Map<K, f> |
Map<K, V> | have f >= (x); | require x.le(f); | Input &Map<K, f> |
Map<K, V> | add f += (x); | assert x.dom().disjoint(f.dom();)update f = f.union_prefer_right(x); | Output Map<K, f> |
Multiset<V> | remove f -= {v}; | require f.count(v) >= 1;update f = f.remove(v); | Input f |
Multiset<V> | have f >= {v}; | require f.count(v) >= 1; | Input &f |
Multiset<V> | add f += {v}; | update f = f.insert(v); | Output f |
Multiset<V> | remove f -= (x); | require x.le(f);update f = f.sub(x); | Input Multiset<f> |
Multiset<V> | have f >= (x); | require x.le(f); | Input &Multiset<f> |
Multiset<V> | add f += (x); | update f = f.add(x); | Output Multiset<f> |
Set<V> | remove f -= {v}; | require f.contains(v);update f = f.remove(v); | Input f |
Set<V> | have f >= {v}; | require f.contains(v); | Input &f |
Set<V> | add f += {v}; | assert !f.contains(v);update f = f.insert(v); | Output f |
Set<V> | remove f -= (x); | require x.subset_of(f);update f = f.difference(x); | Input Set<f> |
Set<V> | have f >= (x); | require x.subset_of(f); | Input &Set<f> |
Set<V> | add f += (x); | assert f.disjoin(t);update f = f.union(x); | Output Set<f> |
nat | remove f -= (x); | require f >= x;update f = f - x; | Input f |
nat | have f >= (x); | require f >= x; | Input &f |
nat | add f += (x); | update f = f + x; | Output f |
bool | remove f -= true; | require f == true;update f = false; | Input f |
bool | have f >= true; | require f == true; | Input &f |
bool | add f += true; | assert f == false;update f = true; | Output f |
bool | remove f -= (x); | require x ==> f;update f = f && !x; | Input Option<f> |
bool | have f >= (x); | require x ==> f; | Input &Option<f> |
bool | add f += (x); | assert !(f && x);update f = f || x; | Output Option<f> |
Persistent Collection Strategies
Verus supports “persistent” versions for several of the collection types:
persistent_option, persistent_map, persistent_set, persistent_count, and persistent_bool.
By “persistent”, we mean that any state introduced is permanent.
persistent_option: once a value becomesSome(x), it will always remainSome(x).persistent_map: once a (key, value) pair is inserted, that key will always remain, and its value will never change.persistent_set: once a value is inserted, that value will remainpersistent_count: the number can never decreasepersistent_bool: once it becomes true, it can never become false.
As a result, we can remove the uniqueness constraints on the tokens,
and we can implement Clone on the token type.
In other words, for a given token (say, token![instance => f => k => v])
we can freely make clones of that token without tracking the number of clones.
| Strategy | a ## b | a · b |
|---|---|---|
persistent_option | a === None || b === None || a === b | if a == None { b } else { a } |
persistent_map | a.agrees(b) | a.union_prefer_right(b) |
persistent_set | true | a.union(b) |
persistent_count | true | max(a, b) |
persistent_bool | true | a || b |
Unlike before, a ## a always holds (with a · a = a).
At a technical level,
this property is what makes it safe to implement Clone on the tokens.
This property also lets us see why we cannot remove state.
These monoids are not cancellative like the above; in particular,
if we have state a and attempt
to “subtract” a, then we might still be left with a.
Thus, from the perspective of the transition system, there can never be any point
to doing a remove.
have and add are specified in the same methodology as above, which amounts to the following:
| Type | Command | Meaning in transition | Exchange Fn Parameter |
|---|---|---|---|
Option<V> | have f >= Some(v); | require f === Some(v); | Input &f |
Option<V> | add f += Some(v); | assert f === None || f === Some(v);update f = Some(v); | Output f |
Option<V> | have f >= (x); | require x === None || f === x; | Input &Option<f> |
Option<V> | add f += (x); | assert f === None || x === None || f === x;update f = if x === None { f } else { x }; | Output Option<f> |
Map<K, V> | have f >= [k => v]; | require f.contains(k) && f.index(k) === v; | Input &f |
Map<K, V> | add f += [k => v]; | assert f.contains(k) ==> f.index(k) === v;update f = f.insert(k, v); | Output f |
Map<K, V> | have f >= (x); | require x.le(f); | Input &Map<K, f> |
Map<K, V> | add f += (x); | assert x.agrees(f)update f = f.union_prefer_right(x); | Output Map<K, f> |
Set<V> | have f >= {v}; | require f.contains(v); | Input &f |
Set<V> | add f += {v}; | update f = f.insert(v); | Output f |
Set<V> | have f >= (x); | require x.subset_of(f); | Input &Set<f> |
Set<V> | add f += (x); | update f = f.union(x); | Output Set<f> |
nat | have f >= (x); | require f >= x; | Input &f |
nat | add f += (x); | update f = max(f, x); | Output f |
bool | have f >= true; | require f == true; | Input &f |
bool | add f += true; | update f = true; | Output f |
bool | have f >= (x); | require x ==> f; | Input &Option<f> |
bool | add f += (x); | update f = f || x | Output Option<f> |
Inherent Safety Conditions
Above, we discussed the general meanings of remove, have, and add, which we repeat here
for reference:
| Command | Meaning as transition on state | Meaning for exchange function |
|---|---|---|
remove f -= (x); | require f >= x;update f = f - x; | Input argument, consumed |
have f >= (x); | require f >= x; | Input argument of type &_ |
add f += (x); | assert f ## x;update f = f · x; | Output argument |
The reader may wonder, why do we use assert for add, but not for the other two?
In the case of remove and have, we allow f >= x to be an enabling condition, and it is then
possible for the client of an exchange function to justify that the enabling condition is met by
the existence of the tokens that it inputs.
In the case of add, however, there is no such justification because the tokens that correspond to x
are output tokens. These tokens do not exist before the transition occurs, so we cannot use their
existence to justify the transition is safe. Rather, it is up to the developer of the transition system
to show that introducing the state given by x is always safe. Hence, we use assert to create a safety condition.
We call this the inherent safety condition of the add command.
As with any ordinary assert, the developer is expected to show that it follows from the invariant
and from any preceeding enabling conditions.
If the proof, does not go through automatically, the developer can supply a proof body using by, e.g.,:
add f += Some(v) by {
// proof that pre.f === None
};Init
TODO