Verus overview
Verus is a tool for verifying the correctness of code written in Rust. The main goal is to verify full functional correctness of low-level systems code, building on ideas from existing verification frameworks like Dafny, Boogie, F*, VCC, Prusti, Creusot, Aeneas, Cogent, Rocq, and Isabelle/HOL. Verification is static: Verus adds no run-time checks, but instead uses computer-aided theorem proving to statically verify that executable Rust code will always satisfy some user-provided specifications for all possible executions of the code.
In more detail, Verus aims to:
- provide a pure mathematical language for expressing specifications (like Dafny, Creusot, F*, Coq, Isabelle/HOL)
- provide a mathematical language for expressing proofs (like Dafny, F*, Coq, Isabelle/HOL) based exclusively on classical logic (like Dafny)
- provide a low-level, imperative language for expressing executable code (like VCC), based on Rust (like Prusti, Creusot, and Aeneas)
- generate small, simple verification conditions that an SMT solver
like Z3 can solve efficiently,
based on the following principles:
- keep the mathematical specification language close to the SMT solver’s mathematical language (like Boogie)
- use lightweight linear type checking, rather than SMT solving, to reason about memory and aliasing (like Cogent, Creusot, Aeneas, and linear Dafny)
We believe that Rust is a good language for achieving these goals. Rust combines low-level data manipulation, including manual memory management, with an advanced, high-level, safe type system. The type system includes features commonly found in higher-level verification languages, including algebraic datatypes (with pattern matching), type classes, and first-class functions. This makes it easy to express specifications and proofs in a natural way. More importantly, Rust’s type system includes sophisticated support for linear types and borrowing, which takes care of much of the reasoning about memory and aliasing. As a result, the remaining reasoning can ignore most memory and aliasing issues, and treat the Rust code as if it were code written in a purely functional language, which makes verification easier.
At present, we do not intend to:
- support all Rust features and libraries (instead, we will focus a high-value features and libraries needed to support our users)
- verify the verifier itself
- verify the Rust/LLVM compilers
This guide
This guide assumes that you’re already somewhat familiar with the basics of Rust programming. (If you’re not, we recommend spending a couple hours on the Learn Rust page.) Familiarity with Rust is useful for Verus, because Verus builds on Rust’s syntax and Rust’s type system to express specifications, proofs, and executable code. In fact, there is no separate language for specifications and proofs; instead, specifications and proofs are written in Rust syntax and type-checked with Rust’s type checker. So if you already know Rust, you’ll have an easier time getting started with Verus.
Nevertheless, verifying the correctness of Rust code requires concepts and techniques
beyond just writing ordinary executable Rust code.
For example, Verus extends Rust’s syntax (via macros) with new concepts for
writing specifications and proofs, such as forall, exists, requires, and ensures,
as well as introducing new types, like the mathematical integer types int and nat.
It can be challenging to prove that a Rust function satisfies its postconditions (its ensures clauses)
or that a call to a function satisfies the function’s preconditions (its requires clauses).
Therefore, this guide’s tutorial will walk you through the various concepts and techniques,
starting with relatively simple concepts (basic proofs about integers),
moving on to more moderately difficult challenges (inductive proofs about data structures),
and then on to more advanced topics such as proofs about arrays using forall and exists
and proofs about concurrent code.
All of these proofs are aided by an automated theorem prover
(specifically, Z3,
a satisfiability-modulo-theories solver, or “SMT solver” for short).
The SMT solver will often be able to prove simple properties,
such as basic properties about booleans or integer arithmetic,
with no additional help from the programmer.
However, more complex proofs often require effort from both the programmer and the SMT solver.
Therefore, this guide will also help you understand the strengths and limitations of SMT solving,
and give advice on how to fill in the parts of proofs that SMT solvers cannot handle automatically.
(For example, SMT solvers usually cannot automatically perform proofs by induction,
but you can write a proof by induction simply by writing a recursive Rust function whose ensures
clause expresses the induction hypothesis.)
Getting Started
In this chapter, we’ll walk you through setting up Verus and running it on a sample program. You can either:
If you don’t want to install Verus yet, but just want to experiment with it or follow along the tutorial, you can also run Verus through the Verus playground in your browser.
Getting started on the command line
1. Install Verus.
To install Verus, follow the instructions at INSTALL.md.
2. Verify a sample program.
Create a file called getting_started.rs, and paste in the following contents:
use vstd::prelude::*;
verus! {
spec fn min(x: int, y: int) -> int {
if x <= y {
x
} else {
y
}
}
fn main() {
assert(min(10, 20) == 10);
assert(min(-10, -20) == -20);
assert(forall|i: int, j: int| min(i, j) <= i && min(i, j) <= j);
assert(forall|i: int, j: int| min(i, j) == i || min(i, j) == j);
assert(forall|i: int, j: int| min(i, j) == min(j, i));
}
} // verus!To run Verus on the file:
If on macOS, Linux, or similar system, run:
/path/to/verus getting_started.rs
If on Windows, run:
.\path\to\verus.exe getting_started.rs
You should see the following output:
note: verifying root module
verification results:: 1 verified, 0 errors
This indicates that Verus successfully verified 1 function (the main function).
Try it on code that won’t verify
If you want, you can try editing the getting_started.rs file
to see a verification failure.
For example, if you add the following line to main:
assert(forall|i: int, j: int| min(i, j) == min(i, i));
you will see an error message:
note: verifying root module
error: assertion failed
--> getting_started.rs:19:12
|
19 | assert(forall|i: int, j: int| min(i, j) == min(i, i));
| ^^^^^^ assertion failed
error: aborting due to previous error
verification results:: 0 verified, 1 errors
3. Compile the program
The command above only verifies the code, but does not compile it. If you also want to compile
it to a binary, you can verus with the --compile flag.
If on macOS, Linux, or similar system, run:
/path/to/verus getting_started.rs --compile
If on Windows, run:
.\path\to\verus.exe getting_started.rs --compile
Either will create a binary getting_started.
However, in this example, the binary won’t do anything interesting
because the main function contains no executable code —
it contains only statically-checked assertions,
which are erased before compilation.
4. Learn more about Verus
Continue with the tutorial, starting with an explanation of the verus! macro from the above example.
Getting started with VSCode
This page will get you set up using Verus in VSCode using the verus-analyzer extension. Note that verus-analyzer is very experimental.
1. Create a Rust crate
Install cargo if you haven’t yet. Find a scratch directory to use, and run:
cargo init verus_test
This will create the following files:
verus_test/Cargo.tomlverus_test/src/main.rs
2. Install verus-analyzer via VSCode
Open VSCode and install verus-analyzer through the VSCode marketplace.
3. Open your workspace in VSCode.
Go to File > Open Folder and select the verus_test directory.
4. Disable rust-analyzer
If you have rust-analyzer installed, you’ll want to disable it, as it is redundant and (without the proper configuration) will result in additional errors that you won’t want to see.
To disable rust-analyzer, go to the extensions panel, find rust-analyzer, click the gear icon, and select “Disable (Workspace)”. (This will disable rust-analyzer only for the current workspace.) Then click the blue “Restart Extensions” button that appears.
5. Test that Verus is working.
Within your verus_test project, navigate to the src/main.rs file. Paste in the following:
use vstd::prelude::*;
verus! {
spec fn min(x: int, y: int) -> int {
if x <= y {
x
} else {
y
}
}
fn main() {
assert(min(10, 20) == 10);
assert(min(-10, -20) == -20);
assert(forall|i: int, j: int| min(i, j) <= i && min(i, j) <= j);
assert(forall|i: int, j: int| min(i, j) == i || min(i, j) == j);
assert(forall|i: int, j: int| min(i, j) == min(j, i));
assert(forall|i: int, j: int| min(i, j) == min(i, i));
}
} // verus!Save the file in order to trigger verus-analyzer.
This program has an error which Verus should detect.
If everything is working correctly, you should see an error from Verus on the final assert line:
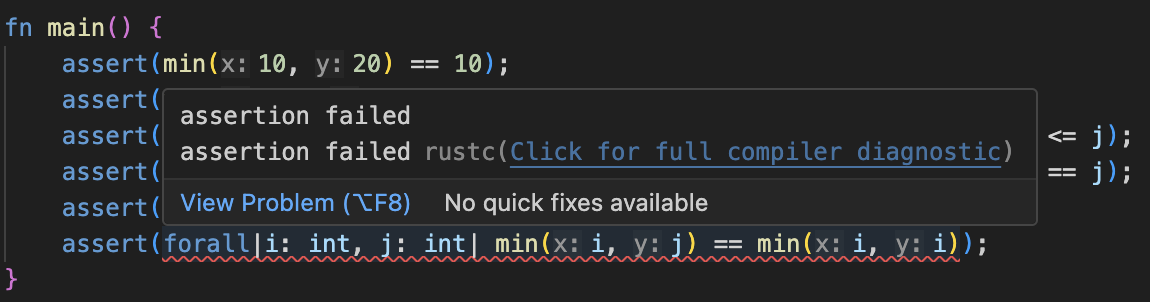
If you click the link, “Click for full compiler diagnostic”, you should see an error like:
error: assertion failed
--> verus_test/src/main.rs:19:12
|
19 | assert(forall|i: int, j: int| min(i, j) == min(i, i));
| ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ assertion failed
Delete this line, and now Verus should say that the file verifies successfully.
6. Learn more about the verus-analyzer extension.
See the verus-analyzer README for more information and tips on using verus-analyzer.
7. Learn more about Verus
Continue with the tutorial, starting with an explanation of the verus! macro from the above example.
The verus! macro
Recall the sample program from the Getting Started chapters:
use vstd::prelude::*;
verus! {
spec fn min(x: int, y: int) -> int {
if x <= y {
x
} else {
y
}
}
fn main() {
assert(min(10, 20) == 10);
assert(min(-10, -20) == -20);
assert(forall|i: int, j: int| min(i, j) <= i && min(i, j) <= j);
assert(forall|i: int, j: int| min(i, j) == i || min(i, j) == j);
assert(forall|i: int, j: int| min(i, j) == min(j, i));
}
} // verus!What is this exactly? Is it Verus? Is it Rust?
It’s both! It’s a Rust source file that uses the verus! macro to embed Verus.
Specifically, the verus! macro extends Rust’s syntax with verification-related features
such as preconditions, postconditions, assertions, forall, exists, etc.,
which we will learn more about in this tutorial.
Verus uses a macro named verus! to extend Rust’s syntax with verification-related features
such as preconditions, postconditions, assertions, forall, exists, etc.
Therefore, each file in a crate will typically take the following form:
use vstd::prelude::*;
verus! {
// ...
}The vstd::prelude exports the verus! macro along with some other Verus utilities.
The verus! macro, besides extending Rust’s syntax, also
tells Verus to verify the functions contained within.
By default, Verus verifies everything inside the verus! macro and ignores anything
defined outside the verus! macro. There are various attributes and directives to modify
this behavior (e.g., see this chapter), but for
most of the tutorial, we will consider all code to be Verus code that must be in the
verus! macro.
Note for the tutorial.
In the remainder of this guide, we will omit these declarations from the examples to avoid clutter.
However, remember that any example code should be placed inside the verus! { ... } block,
and that the file should contain use vstd::prelude::*;.
Alternate syntax.
Verus also supports an alternate, attribute-based syntax.
This syntax may be helpful when you want to minimize changes to an existing Rust project.
However, because the verus! syntax is cleaner and simpler, we’ll stick to that in this
tutorial.
Basic specifications
Verus programs contain specifications to describe the intended behavior of the code. These specifications include preconditions, postconditions, assertions, and loop invariants. Specifications are one form of ghost code — code that appears in the Rust source code for verification’s sake, but does not appear in the compiled executable.
This chapter will walk through some basic examples of preconditions, postconditions, and assertions, showing the syntax for writing these specifications and discussing integer arithmetic and equality in specifications.
Preconditions (requires clauses)
Let’s start with a small example.
Suppose we want to verify a function octuple that multiplies a number by 8:
fn octuple(x1: i8) -> i8 {
let x2 = x1 + x1;
let x4 = x2 + x2;
x4 + x4
}If we ask Verus to verify this code, Verus immediately reports errors about octuple:
error: possible arithmetic underflow/overflow
|
| let x2 = x1 + x1;
| ^^^^^^^
Here, Verus cannot prove that the result of x1 + x1 fits in an 8-bit i8 value,
which allows values in the range -128…127.
If x1 were 100, for example, x1 + x1 would be 200, which is larger than 127.
We need to make sure that when octuple is called, the argument x1 is not too large.
We can do this by adding preconditions (also known as “requires clauses”)
to octuple specifying which values for x1 are allowed.
In Verus, preconditions are written with a requires followed by zero or more boolean expressions
separated by commas:
fn octuple(x1: i8) -> i8
requires
-64 <= x1,
x1 < 64,
{
let x2 = x1 + x1;
let x4 = x2 + x2;
x4 + x4
}The two preconditions above say that x1 must be at least -64 and less than 64,
so that x1 + x1 will fit in the range -128…127.
This fixes the error about x1 + x1, but we still get an error about x2 + x2:
error: possible arithmetic underflow/overflow
|
| let x4 = x2 + x2;
| ^^^^^^^
If we want x1 + x1, x2 + x2, and x4 + x4 to all succeed, we need a tighter bound on x1:
fn octuple(x1: i8) -> i8
requires
-16 <= x1,
x1 < 16,
{
let x2 = x1 + x1;
let x4 = x2 + x2;
x4 + x4
}This time, verification is successful.
Now suppose we try to call octuple with a value that does not satisfy octuple’s precondition:
fn main() {
let n = octuple(20);
}For this call, Verus reports an error, since 20 is not less than 16:
error: precondition not satisfied
|
| x1 < 16,
| ------- failed precondition
...
| let n = octuple(20);
| ^^^^^^^^^^^
If we pass 10 instead of 20, verification succeeds:
fn main() {
let n = octuple(10);
}Postconditions (ensures clauses)
Suppose we want to verify properties about the value returned from octuple.
For example, we might want to assert that the value returned from octuple
is 8 times as large as the argument passed to octuple.
Let’s try putting an assertion in main that the result of calling octuple(10) is 80:
fn main() {
let n = octuple(10);
assert(n == 80);
}Although octuple(10) really does return 80,
Verus nevertheless reports an error:
error: assertion failed
|
| assert(n == 80);
| ^^^^^^^ assertion failed
The error occurs because, even though octuple multiplies its argument by 8,
octuple doesn’t publicize this fact to the other functions in the program.
To do this, we can add postconditions (ensures clauses) to octuple specifying
some properties of octuple’s return value:
fn octuple(x1: i8) -> (x8: i8)
requires
-16 <= x1,
x1 < 16,
ensures
x8 == 8 * x1,
{
let x2 = x1 + x1;
let x4 = x2 + x2;
x4 + x4
}To write a property about the return value, we need to give a name to the return value.
The Verus syntax for this is -> (name: return_type). In the example above,
saying -> (x8: i8) allows the postcondition x8 == 8 * x1 to use the name x8
for octuple’s return value.
Preconditions and postconditions establish a modular verification protocol between functions.
When main calls octuple, Verus checks that the arguments in the call satisfy octuple’s
preconditions.
When Verus verifies the body of the octuple function,
it can assume that the preconditions are satisfied,
without having to know anything about the exact arguments passed in by main.
Likewise, when Verus verifies the body of the main function,
it can assume that octuple satisfies its postconditions,
without having to know anything about the body of octuple.
In this way, Verus can verify each function independently.
This modular verification approach breaks verification into small, manageable pieces,
which makes verification more efficient than if Verus tried to verify
all of a program’s functions together simultaneously.
Nevertheless, writing preconditions and postconditions requires significant programmer effort —
if you want to verify a large program with a lot of functions,
you’ll probably spend substantial time writing preconditions and postconditions for the functions.
assert and assume
While requires and ensures connect functions together,
assert makes a local, private request to the SMT solver to prove a certain fact.
(Note: assert(...) should not be confused with the Rust assert!(...) macro —
the former is statically checked using the SMT solver, while the latter is checked at run-time.)
assert has an evil twin named assume, which asks the SMT solver to
simply accept some boolean expression as a fact without proof.
While assert is harmless and won’t cause any unsoundness in a proof,
assume can easily enable a “proof” of a fact that isn’t true.
In fact, by writing assume(false), you can prove anything you want:
assume(false);
assert(2 + 2 == 5); // succeedsVerus programmers often use assert and assume to help develop and debug proofs.
They may add temporary asserts to determine which facts the SMT solver can prove
and which it can’t,
and they may add temporary assumes to see which additional assumptions are necessary
for the SMT solver to complete a proof,
or as a placeholder for parts of the proof that haven’t yet been written.
As the proof evolves, the programmer replaces assumes with asserts,
and may eventually remove the asserts.
A complete proof may contain asserts, but should not contain any assumes.
(In some situations, assert can help the SMT solver complete a proof,
by giving the SMT hints about how to manipulate forall and exists expressions.
There are also special forms of assert, such as assert(...) by(bit_vector),
to help prove properties about bit vectors, nonlinear integer arithmetic,
forall expressions, etc.)
Executable code and ghost code
Let’s put everything from this section together into a final version of our example program:
use vstd::prelude::*;
verus! {
#[verifier::external_body]
fn print_two_digit_number(i: i8)
requires
-99 <= i < 100,
{
println!("The answer is {}", i);
}
fn octuple(x1: i8) -> (x8: i8)
requires
-16 <= x1 < 16,
ensures
x8 == 8 * x1,
{
let x2 = x1 + x1;
let x4 = x2 + x2;
x4 + x4
}
fn main() {
let n = octuple(10);
assert(n == 80);
print_two_digit_number(n);
}
} // verus!Here, we’ve made a few final adjustments.
First, we’ve combined the two preconditions -16 <= x1 and x1 < 16
into a single preconditon -16 <= x1 < 16,
since Verus lets us chain multiple inequalities together in a single expression
(equivalently, we could have also written -16 <= x1 && x1 < 16).
Second, we’ve added a function print_two_digit_number to print the result of octuple.
Unlike main and octuple, we ask Verus not to verify print_two_digit_number.
We do this by marking it #[verifier::external_body],
so that Verus pays attention to the function’s preconditions and postconditions but ignores
the function’s body.
This is common in projects using Verus:
you may want to verify some of it (perhaps the program’s core algorithms),
but leave other aspects, such as input-output operations, unverified.
More generally, since verifying all the software in the world is still infeasible,
there will be some boundary between verified code and unverified code,
and #[verifier::external_body] can be used to mark this boundary.
We can now compile the program above using the --compile option to Verus:
./target-verus/release/verus --compile ../examples/guide/requires_ensures.rs
This will produce an executable that prints a message when run:
The answer is 80
Note that the generated executable does not contain the requires, ensures, and assert code,
since these are only needed during static verification,
not during run-time execution.
We refer to requires, ensures, assert, and assume as ghost code,
in contast to the executable code that actually gets compiled.
Verus erases all ghost code before compilation so that it imposes no run-time overhead.
Expressions and operators for specifications
Verus extends Rust’s syntax with additional operators and expressions useful for writing specifications. For example:
forall|i: int, j: int| 0 <= i <= j < len ==> f(i, j)This snippet illustrates:
- the
forallquantifier, which we will cover later - chained operators
- implication operators
Here, we’ll discuss the last two, along with Verus notation for conjunction, disjunction, and field access.
Chained inequalities
Specifications can chain together multiple <=, <, >=, and > operations.
For example,
0 <= i <= j < len has the same meaning as 0 <= i && i <= j && j < len.
Logical implication
To make specifications more readable, Verus supports an implication operator ==>.
The expression a ==> b (pronounced “a implies b”) is logically equivalent to !a || b.
As an example, the expression
forall|i: int, j: int| 0 <= i <= j < len ==> f(i, j)
means that for every pair i and j such that 0 <= i <= j < len, f(i, j) is true.
Note that ==> has lower precedence that most other boolean operations.
For example, a ==> b && c means a ==> (b && c).
Verus also supports two-way implication for booleans (<==>) with even lower precedence,
so that a <==> b && c is equivalent to a == (b && c).
See the reference for a full description of precedence
in Verus.
Conjunction and disjunction
Because &&, ||, and ==> are so common in Verus specifications, it is often desirable to have
low precedence versions of && and ||. Verus also supports “triple-and” (&&&) and
“triple-or” (|||) which are equivalent to && and || except for their precedence.
Implication ==> and equivalence <==> bind more tightly than either &&& or |||.
&&& and ||| are also convenient for the “bulleted list” form:
&&& a ==> b
&&& c
&&& d <==> e && f
This has the same meaning as (a ==> b) && c && (d <==> (e && f)).
Accessing fields of a struct or enum
Verus has ->, is, and matches syntax for accessing fields
of structs
and matching variants of enums.
Integer types
Rust supports various fixed-bit-width integer types:
i8,i16,i32,i64,i128,isizeu8,u16,u32,u64,u128,usize
To these, Verus adds two more integer types to represent arbitrarily large integers in specifications:
- int
- nat
The type int is the most fundamental type for reasoning about integer arithmetic in Verus.
It represents all mathematical integers,
both positive and negative.
The SMT solver contains direct support for reasoning about values of type int.
Internally, Verus uses int to represent the other integer types,
adding mathematical constraints to limit the range of the integers.
For example, a value of the type nat of natural numbers
is a mathematical integer constrained to be greater than or equal to 0.
Rust’s fixed-bit-width integer types have both a lower and upper bound;
a u8 value is an integer constrained to be greater than or equal to 0 and less than 256:
fn test_u8(u: u8) {
assert(0 <= u < 256);
}The bounds of usize and isize are platform dependent.
By default, Verus assumes that these types may be either 32 bits or 64 bits wide,
but this assumption may be configured.
Verus recognizes the constants
usize::BITS,
usize::MAX,
isize::MAX,
and
isize::MIN,
which are useful for reasoning symbolically
about the usize integer range.
Using integer types in specifications
Since there are 14 different integer types (counting int, nat, u8…usize, and i8…isize),
it’s not always obvious which type to use when writing a specification.
Our advice is to be as general as possible by default:
- Use
intby default, since this is the most general type and is supported most efficiently by the SMT solver.- Example: the Verus sequence library
uses
intfor most operations, such as indexing into a sequence. - Note: as discussed below, most arithmetic operations in specifications produce values of type
int, so it is usually most convenient to write specifications in terms ofint.
- Example: the Verus sequence library
uses
- Use
natfor return values and datatype fields where the 0 lower bound is likely to provide useful information, such as lengths of sequences.- Example: the Verus
Seq::len()function returns anatto represent the length of a sequence. - The type
natis also handy for proving that recursive definitions terminate; you might to define a recursivefactorialfunction to take a parameter of typenat, if you don’t want to provide a definition offactorialfor negative integers.
- Example: the Verus
- Use fixed-width integer types for fixed-with values such as bytes.
- Example: the bytes of a network packet can be represented with type
Seq<u8>, an arbitrary-length sequence of 8-bit values.
- Example: the bytes of a network packet can be represented with type
Note that int and nat are usable only in ghost code;
they cannot be compiled to executable code.
For example, the following will not work:
fn main() {
let i: int = 5; // FAILS: executable variable `i` cannot have type `int`, which is ghost-only
}Integer constants
As in ordinary Rust, integer constants in Verus can include their type as a suffix
(e.g. 7u8 or 7u32 or 7int) to precisely specify the type of the constant:
fn test_consts() {
let u: u8 = 1u8;
assert({
let i: int = 2int;
let n: nat = 3nat;
0int <= u < i < n < 4int
});
}Usually, but not always, Verus and Rust will be able to infer types for integer constants, so that you can omit the suffixes unless the Rust type checker complains about not being able to infer the type:
fn test_consts_infer() {
let u: u8 = 1;
assert({
let i: int = 2;
let n: nat = 3;
0 <= u < i < n < 4
});
}Note that the values 0, u, i, n, and 4 in the expression 0 <= u < i < n < 4
are allowed to all have different types —
you can use <=, <, >=, >, ==, and != to compare values of different integer types inside ghost code
(e.g. comparing a u8 to an int in u < i).
Constants with the suffix int and nat can be arbitrarily large:
fn test_consts_large() {
assert({
let i: int = 0x10000000000000000000000000000000000000000000000000000000000000000int;
let j: int = i + i;
j == 2 * i
});
}Integer coercions using “as”
As in ordinary rust, the as operator coerces one integer type to another.
In ghost code, you can use as int or as nat to coerce to int or nat:
fn test_coerce() {
let u: u8 = 1;
assert({
let i: int = u as int;
let n: nat = u as nat;
u == i && u == n
});
}You can use as to coerce a value v to a type t even if v is too small or too large to fit in t.
However, if the value v is outside the bounds of type t,
then the expression v as t will produce some arbitrary value of type t:
fn test_coerce_fail() {
let v: u16 = 257;
let u: u8 = v as u8;
assert(u == v); // FAILS, because u has type u8 and therefore cannot be equal to 257
}This produces an error for the assertion, along with a hint that the value in the as coercion might have been out of range:
error: assertion failed
|
| assert(u == v); // FAILS, because u has type u8 and therefore cannot be equal to 257
| ^^^^^^ assertion failed
note: recommendation not met: value may be out of range of the target type (use `#[verifier::truncate]` on the cast to silence this warning)
|
| let u: u8 = v as u8;
| ^
See the reference for more on how Verus defines as-truncation and how to reason about it.
Integer arithmetic
Integer arithmetic behaves a bit differently in ghost code than in executable code.
In executable code, we frequently have to reason about integer overflow, and in fact, Verus requires us to prove the absence of overflow. The following operation fails because the arithmetic might produce an operation greater than 255:
fn test_sum(x: u8, y: u8) {
let sum1: u8 = x + y; // FAILS: possible overflow
}error: possible arithmetic underflow/overflow
|
| let sum1: u8 = x + y; // FAILS: possible overflow
| ^^^^^
In ghost code, however,
common arithmetic operations
(+, -, *, /, %) never overflow or wrap.
To make this possible, Verus widens the results of many operations;
for example, adding two u8 values is widened to type int.
fn test_sum2(x: u8, y: u8) {
assert({
let sum2: int = x + y; // in ghost code, + returns int and does not overflow
0 <= sum2 < 511
});
}Since + does not overflow in ghost code, we can easily write specifications about overflow.
For example, to make sure that the executable x + y doesn’t overflow,
we simply write requires x + y < 256, relying on the fact that x + y is widened to type int
in the requires clause:
fn test_sum3(x: u8, y: u8)
requires
x + y < 256, // make sure "let sum1: u8 = x + y" can't overflow
{
let sum1: u8 = x + y; // succeeds
}Also note that the inputs need not have the same type; you can add, subtract, or multiply one integer type with another:
fn test_sum_mixed(x: u8, y: u16) {
assert(x + y >= y); // x + y has type int, so the assertion succeeds
assert(x - y <= x); // x - y has type int, so the assertion succeeds
}In general in ghost code,
Verus widens native Rust integer types to int for operators like +, -, and * that might overflow;
the reference page describes the widening rules in more detail.
Here are some more tips to keep in mind:
- In ghost code,
/and%compute Euclidean division and remainder, rather than Rust’s truncating division and remainder, when operating on negative left-hand sides or negative right-hand sides. - Division-by-0 and mod-by-0 are errors in executable code and are unspecified in ghost code (see Ghost code vs. exec code for more detail).
- The named arithmetic functions,
add(x, y),sub(x, y), andmul(x, y), do not perform widening, and thus have truncating behavior, even in ghost code. Verus also recognizes some Rust functions likewrapped_addandchecked_add, which may be used in either executable or ghost code.
Equality
Equality behaves differently in ghost code than in executable code.
In executable code, Rust defines == to mean a call to the eq function of the PartialEq trait:
fn equal1(x: u8, y: u8) {
let eq1 = x == y; // means x.eq(y) in Rust
let eq2 = y == x; // means y.eq(x) in Rust
assert(eq1 ==> eq2); // succeeds
}For built-in integer types like u8, the x.eq(y) function is defined as we’d expect,
returning true if x and y hold the same integers.
For user-defined types, though, eq could have other behaviors:
it might have side effects, behave nondeterministically,
or fail to fulfill its promise to implement an
equivalence relation,
even if the type implements the Rust Eq trait:
fn equal2<A: Eq>(x: A, y: A) {
let eq1 = x == y; // means x.eq(y) in Rust
let eq2 = y == x; // means y.eq(x) in Rust
assert(eq1 ==> eq2); // won't work; we can't be sure that A is an equivalence relation
}In ghost code, by contrast, the == operator is always an equivalence relation
(i.e. it is reflexive, symmetric, and transitive):
fn equal3(x: u8, y: u8) {
assert({
let eq1 = x == y;
let eq2 = y == x;
eq1 ==> eq2
});
}Verus defines == in ghost code to be true when:
- for two integers or booleans, the values are equal
- for two structs or enums, the types are the same and the fields are equal
- for two
&references, two Box values, two Rc values, or two Arc values, the pointed-to values are the same - for two RefCell values or two Cell values, the pointers to the interior data are equal (not the interior contents)
In addition, collection dataypes such as Seq<T>, Set<T>, and Map<Key, Value>
have their own definitions of ==,
where two sequences, two sets, or two maps are equal if their elements are equal.
As explained more in specification libraries and extensional equality,
these sometimes require the “extensional equality” operator =~= to help prove equality
between two sequences, two sets, or two maps.
Specification code, proof code, executable code
Verus classifies code into three modes: spec, proof, and exec,
where:
speccode describes properties about programsproofcode proves that programs satisfy propertiesexeccode is ordinary Rust code that can be compiled and run
Both spec code and proof code are forms of ghost code,
so we can organize the three modes in a hierarchy:
- code
- ghost code
speccodeproofcode
execcode
- ghost code
Every function in Verus is either a spec function, a proof function, or an exec function:
spec fn f1(x: int) -> int {
x / 2
}
proof fn f2(x: int) -> int {
x / 2
}
// "exec" is optional, and is usually omitted
exec fn f3(x: u64) -> u64 {
x / 2
}
exec is the default function annotation, so it is usually omitted:
fn f3(x: u64) -> u64 { x / 2 } // exec functionThe rest of this chapter will discuss these three modes in more detail. As you read, you can keep in mind the following relationships between the three modes:
| spec code | proof code | exec code | |
|---|---|---|---|
can contain spec code, call spec functions | yes | yes | yes |
can contain proof code, call proof functions | no | yes | yes |
can contain exec code, call exec functions | no | no | yes |
spec functions
Let’s start with a simple spec function that computes the minimum of two integers:
spec fn min(x: int, y: int) -> int {
if x <= y {
x
} else {
y
}
}
fn test() {
assert(min(10, 20) == 10); // succeeds
assert(min(100, 200) == 100); // succeeds
}Unlike exec functions,
the bodies of spec functions are visible to other functions in the same module,
so the test function can see inside the min function,
which allows the assertions in test to succeed.
Across modules, the bodies of spec functions can be made public to other modules
or kept private to the current module.
The body is public if the function is marked open,
allowing assertions about the function’s body to succeed in other modules:
mod M1 {
use verus_builtin::*;
pub open spec fn min(x: int, y: int) -> int {
if x <= y {
x
} else {
y
}
}
}
mod M2 {
use verus_builtin::*;
use crate::M1::*;
fn test() {
assert(min(10, 20) == 10); // succeeds
}
}By contrast, if the function is marked closed,
then other modules cannot see the function’s body,
even if they can see the function’s declaration. However,
functions within the same module can view a closed spec fn’s body.
In other words, pub makes the declaration public,
while open and closed make the body public or private.
All pub spec functions must be marked either open or closed;
Verus will complain if the function lacks this annotation.
mod M1 {
use verus_builtin::*;
pub closed spec fn min(x: int, y: int) -> int {
if x <= y {
x
} else {
y
}
}
pub proof fn lemma_min(x: int, y: int)
ensures
min(x,y) <= x && min(x,y) <= y,
{}
}
mod M2 {
use verus_builtin::*;
use crate::M1::*;
fn test() {
assert(min(10, 20) == min(10, 20)); // succeeds
assert(min(10, 20) == 10); // FAILS
proof {
lemma_min(10,20);
}
assert(min(10, 20) <= 10); // succeeds
}
}In the example above with min being closed,
the module M2 can still talk about the function min,
proving, for example, that min(10, 20) equals itself
(because everything equals itself, regardless of what’s in it’s body).
On the other hand, the assertion that min(10, 20) == 10 fails,
because M2 cannot see min’s body and therefore doesn’t know that min
computes the minimum of two numbers:
error: assertion failed
|
| assert(min(10, 20) == 10); // FAILS
| ^^^^^^^^^^^^^^^^^ assertion failed
After the call to lemma_min, the assertion that min(10, 20) <= 10 succeeds because lemma_min exposes min(x,y) <= x as a post-condition. lemma_min can prove because this postcondition because it can see the body of min despite min being closed, as lemma_min and min are in the same module.
You can think of pub open spec functions as defining abbreviations
and pub closed spec functions as defining abstractions.
Both can be useful, depending on the situation.
spec functions may be called from other spec functions
and from specifications inside exec functions,
such as preconditions and postconditions.
For example, we can define the minimum of three numbers, min3,
in terms of the mininum of two numbers.
We can then define an exec function, compute_min3,
that uses imperative code with mutable updates to compute
the minimum of 3 numbers,
and defines its postcondition in terms of the spec function min3:
spec fn min(x: int, y: int) -> int {
if x <= y {
x
} else {
y
}
}
spec fn min3(x: int, y: int, z: int) -> int {
min(x, min(y, z))
}
fn compute_min3(x: u64, y: u64, z: u64) -> (m: u64)
ensures
m == min3(x as int, y as int, z as int),
{
let mut m = x;
if y < m {
m = y;
}
if z < m {
m = z;
}
m
}
fn test() {
let m = compute_min3(10, 20, 30);
assert(m == 10);
}
The difference between min3 and compute_min3 highlights some differences
between spec code and exec code.
While exec code may use imperative language features like mutation,
spec code is restricted to purely functional mathematical code.
On the other hand, spec code is allowed to use int and nat,
while exec code is restricted to compilable types like u64.
proof functions
Consider the pub closed spec min function from the previous section.
This defined an abstract min function without revealing the internal
definition of min to other modules.
However, an abstract function definition is useless unless we can say something about the function.
For this, we can use a proof function.
In general, proof functions will reveal or prove properties about specifications.
In this example, we’ll define a proof function named lemma_min that
reveals properties about min without revealing the exact definition of min.
Specifically, lemma_min reveals that min(x, y) equals either x or y and
is no larger than x and y:
mod M1 {
use verus_builtin::*;
pub closed spec fn min(x: int, y: int) -> int {
if x <= y {
x
} else {
y
}
}
pub proof fn lemma_min(x: int, y: int)
ensures
min(x, y) <= x,
min(x, y) <= y,
min(x, y) == x || min(x, y) == y,
{
}
}
mod M2 {
use verus_builtin::*;
use crate::M1::*;
proof fn test() {
lemma_min(10, 20);
assert(min(10, 20) == 10); // succeeds
assert(min(100, 200) == 100); // FAILS
}
}Like exec functions, proof functions may have requires and ensures clauses.
Unlike exec functions, proof functions are ghost and are not compiled to executable code.
In the example above, the lemma_min(10, 20) function is used to help the function test in module M2
prove an assertion about min(10, 20), even when M2 cannot see the internal definition of min
because min is closed.
On the other hand, the assertion about min(100, 200) still fails
unless test also calls lemma_min(100, 200).
proof blocks
Ultimately, the purpose of spec functions and proof functions is to help prove
properties about executable code in exec functions.
In fact, exec functions can contain pieces of proof code in proof blocks,
written with proof { ... }.
Just like a proof function contains proof code,
a proof block in an exec function contains proof code
and can use all of the ghost code features that proof functions can use,
such as the int and nat types.
Consider an earlier example that introduced variables inside an assertion:
fn test_consts_infer() {
let u: u8 = 1;
assert({
let i: int = 2;
let n: nat = 3;
0 <= u < i < n < 4
});
}We can write this in a more natural style using a proof block:
fn test_consts_infer() {
let u: u8 = 1;
proof {
let i: int = 2;
let n: nat = 3;
assert(0 <= u < i < n < 4);
}
}
Here, the proof code inside the proof block can create local variables
of type int and nat,
which can then be used in a subsequent assertion.
The entire proof block is ghost code, so all of it, including its local variables,
will be erased before compilation to executable code.
Proof blocks can call proof functions.
In fact, any calls from an exec function to a proof function
must appear inside proof code such as a proof block,
rather than being called directly from the exec function’s exec code.
This helps clarify which code is executable and which code is ghost,
both for the compiler and for programmers reading the code.
In the exec function test shown below,
a proof block is used to call lemma_min,
allowing subsequent assertions about min to succeed.
mod M1 {
use verus_builtin::*;
pub closed spec fn min(x: int, y: int) -> int {
if x <= y {
x
} else {
y
}
}
pub proof fn lemma_min(x: int, y: int)
ensures
min(x, y) <= x,
min(x, y) <= y,
min(x, y) == x || min(x, y) == y,
{
}
}
mod M2 {
use verus_builtin::*;
use crate::M1::*;
fn test() {
proof {
lemma_min(10, 20);
lemma_min(100, 200);
}
assert(min(10, 20) == 10); // succeeds
assert(min(100, 200) == 100); // succeeds
}
}
assert-by
Notice that in the previous example,
the information that test gains about min
is not confined to the proof block,
but instead propagates past the end of the proof block
to help prove the subsequent assertions.
This is often useful,
particularly when the proof block helps
prove preconditions to subsequent calls to exec functions,
which must appear outside the proof block.
However, sometimes we only need to prove information for a specific purpose,
and it clarifies the structure of the code if we limit the scope
of the information gained.
For this reason,
Verus supports assert(...) by { ... } expressions,
which allows proof code inside the by { ... } block whose sole purpose
is to prove the asserted expression in the assert(...).
Any additional information gained in the proof code is limited to the scope of the block
and does not propagate outside the assert(...) by { ... } expression.
In the example below,
the proof code in the block calls both lemma_min(10, 20) and lemma_min(100, 200).
The first call is used to prove min(10, 20) == 10 in the assert(...) by { ... } expression.
Once this is proven, the subsequent assertion assert(min(10, 20) == 10); succeeds.
However, the assertion assert(min(100, 200) == 100); fails,
because the information gained by the lemma_min(100, 200) call
does not propagate outside the block that contains the call.
mod M1 {
use verus_builtin::*;
pub closed spec fn min(x: int, y: int) -> int {
if x <= y {
x
} else {
y
}
}
pub proof fn lemma_min(x: int, y: int)
ensures
min(x, y) <= x,
min(x, y) <= y,
min(x, y) == x || min(x, y) == y,
{
}
}
mod M2 {
use verus_builtin::*;
use crate::M1::*;
fn test() {
assert(min(10, 20) == 10) by {
lemma_min(10, 20);
lemma_min(100, 200);
}
assert(min(10, 20) == 10); // succeeds
assert(min(100, 200) == 100); // FAILS
}
}spec functions vs. proof functions
Now that we’ve seen both spec functions and proof functions,
let’s take a longer look at the differences between them.
We can summarize the differences in the following table
(including exec functions in the table for reference):
| spec function | proof function | exec function | |
|---|---|---|---|
| compiled or ghost | ghost | ghost | compiled |
| code style | purely functional | mutation allowed | mutation allowed |
can call spec functions | yes | yes | yes |
can call proof functions | no | yes | yes |
can call exec functions | no | no | yes |
| body visibility | may be visible | never visible | never visible |
| body | body optional | body mandatory | body mandatory |
| determinism | deterministic | nondeterministic | nondeterministic |
| preconditions/postconditions | recommends | requires/ensures | requires/ensures |
As described in the spec functions section,
spec functions make their bodies visible to other functions in their module
and may optionally make their bodies visible to other modules as well.
spec functions can also omit their bodies entirely:
spec fn f(i: int) -> int;
Such an uninterpreted function can be useful in libraries that define an abstract, uninterpreted function along with trusted axioms about the function.
Determinism
spec functions are deterministic:
given the same arguments, they always return the same result.
Code can take advantage of this determinism even when a function’s body
is not visible.
For example, the assertion x1 == x2 succeeds in the code below,
because both x1 and x2 equal s(10),
and s(10) always produces the same result, because s is a spec function:
mod M1 {
use verus_builtin::*;
pub closed spec fn s(i: int) -> int {
i + 1
}
pub proof fn p(i: int) -> int {
i + 1
}
}
mod M2 {
use verus_builtin::*;
use crate::M1::*;
proof fn test_determinism() {
let s1 = s(10);
let s2 = s(10);
assert(s1 == s2); // succeeds
let p1 = p(10);
let p2 = p(10);
assert(p1 == p2); // FAILS
}
}By contrast, the proof function p is, in principle,
allowed to return different results each time it is called,
so the assertion p1 == p2 fails.
(Nondeterminism is common for exec functions
that perform input-output operations or work with random numbers.
In practice, it would be unusual for a proof function to behave nondeterministically,
but it is allowed.)
recommends
exec functions and proof functions can have requires and ensures clauses.
By contrast, spec functions cannot have requires and ensures clauses.
This is similar to the way Boogie works,
but differs from other systems like Dafny
and F*.
The reason for disallowing requires and ensures is to keep Verus’s specification language
close to the SMT solver’s mathematical language in order to use the SMT solver as efficiently
as possible (see the Verus Overview).
Nevertheless, it’s sometimes useful to have some sort of preconditions on spec functions
to help catch mistakes in specifications early or to catch accidental misuses of spec functions.
Therefore, spec functions may contain recommends clauses
that are similar to requires clauses,
but represent just lightweight recommendations rather than hard requirements.
For example, for the following function,
callers are under no obligation to obey the i > 0 recommendation:
spec fn f(i: nat) -> nat
recommends
i > 0,
{
(i - 1) as nat
}
proof fn test1() {
assert(f(0) == f(0)); // succeeds
}
It’s perfectly legal for test1 to call f(0), and no error or warning will be generated for f
(in fact, Verus will not check the recommendation at all).
However, if there’s a verification error in a function,
Verus will automatically rerun the verification with recommendation checking turned on,
in hopes that any recommendation failures will help diagnose the verification failure.
For example, in the following:
proof fn test2() {
assert(f(0) <= f(1)); // FAILS
}Verus print the failed assertion as an error and then prints the failed recommendation as a note:
error: assertion failed
|
| assert(f(0) <= f(1)); // FAILS
| ^^^^^^^^^^^^ assertion failed
note: recommendation not met
|
| recommends i > 0
| ----- recommendation not met
...
| assert(f(0) <= f(1)); // FAILS
| ^^^^^^^^^^^^
If the note isn’t helpful, programmers are free to ignore it.
By default, Verus does not perform recommends checking on calls from spec functions:
spec fn caller1() -> nat {
f(0) // no note, warning, or error generated
}
However, you can write spec(checked) to request recommends checking,
which will cause Verus to generate warnings for recommends violations:
spec(checked) fn caller2() -> nat {
f(0) // generates a warning because of "(checked)"
}
This is particularly useful for specifications that are part of the “trusted computing base” that describes the interface to external, unverified components.
Ghost code vs. exec code
The purpose of exec code is to manipulate physically real values —
values that exist in physical electronic circuits when a program runs.
The purpose of ghost code, on the other hand,
is merely to talk about the values that exec code manipulates.
In a sense, this gives ghost code supernatural abilities:
ghost code can talk about things that could not be physically implemented at run-time.
We’ve already seen one example of this with the types int and nat,
which can only be used in ghost code.
As another example, ghost code can talk about the result of division by zero:
fn divide_by_zero() {
let x: u8 = 1;
assert(x / 0 == x / 0); // succeeds in ghost code
let y = x / 0; // FAILS in exec code
}This simply reflects the SMT solver’s willingness to reason about the result of division by zero
as an unspecified integer value.
By contrast, Verus reports a verification failure if exec code attempts to divide by zero:
error: possible division by zero
|
| let y = x / 0; // FAILS
| ^^^^^
Two particular abilities of ghost code1 are worth keeping in mind:
- Ghost code can copy values of any type,
even if the type doesn’t implement the Rust
Copytrait. - Ghost code can create a value of any type2, even if the type has no public constructors (e.g. even if the type is struct whose fields are all private to another module).
For example, the following spec functions create and duplicate values of type S,
defined in another module with private fields and without the Copy trait:
mod MA {
// does not implement Copy
// does not allow construction by other modules
pub struct S {
private_field: u8,
}
}
mod MB {
use verus_builtin::*;
use crate::MA::*;
// construct a ghost S
spec fn make_S() -> S;
// duplicate an S
spec fn duplicate_S(s: S) -> (S, S) {
(s, s)
}
}
These operations are not allowed in exec code.
Furthermore, values from ghost code are not allowed to leak into exec code —
what happens in ghost code stays in ghost code.
Any attempt to use a value from ghost code in exec code will result in a compile-time error:
fn test(s: S) {
let pair = duplicate_S(s); // FAILS
}error: cannot call function with mode spec
|
| let pair = duplicate_S(s); // FAILS
| ^^^^^^^^^^^^^^
As an example of ghost code that uses these abilities,
a call to the Verus Seq::index(...) function
can duplicate a value from the sequence, if the index i is within bounds,
and create a value out of thin air if i is out of bounds:
impl<A> Seq<A> {
...
/// Gets the value at the given index `i`.
///
/// If `i` is not in the range `[0, self.len())`, then the resulting value
/// is meaningless and arbitrary.
pub spec fn index(self, i: int) -> A
recommends 0 <= i < self.len();
...
}Producing exec code from spec code (and vice versa)
Thanks to various contributions from the Verus community, Verus can, in some cases, automatically produce an exec function that provably implements a spec function. Conversely, in some cases, it can automatically produce a spec function from an exec function.
-
Variables in
proofcode can opt out of these special abilities using thetrackedannotation, but this is an advanced feature that can be ignored for now. ↩ -
This is true even if the type has no values in
execcode, like the Rust!“never” type (see the “bottom” value in this technical discussion). ↩
const declarations
In Verus, const declarations are treated internally as 0-argument function calls.
Thus just like functions, const declarations can be marked spec, proof, exec,
or left without an explicit mode.
By default, a const without an explicit mode is assigned a dual spec/exec mode.
We’ll go through what each of these modes mean.
spec consts
A spec const is like a spec function with no arguments.
It is always ghost and cannot be used as an exec value.
spec const SPEC_ONE: int = 1;
spec fn spec_add_one(x: int) -> int {
x + SPEC_ONE
}
proof and exec consts
Just as proof and exec functions can have ensures clauses specifying a postcondition,
proof and exec consts can have ensures clauses to tie the declaration to a spec expression.
The syntax follows the syntax of a function definition.
exec const C: u64
ensures
C == 7,
{
7
}
Note here that we can also use assert when defining the const,
and that we can define it using a call to another const function.
spec fn f() -> int {
1
}
const fn e() -> (u: u64)
ensures
u == f(),
{
1
}
exec const E: u64
ensures
E == 2,
{
assert(f() == 1);
1 + e()
}
spec/exec consts
A const without an explicit mode is dual-use:
it is usable as both an exec value and a spec value.
const ONE: u8 = 1;
fn add_one(x: u8) -> (ret: u8)
requires
x < 0xff,
ensures
ret == x + ONE, // use "ONE" in spec code
{
x + ONE // use "ONE" in exec code
}
Therefore, the const definition is restricted to obey the rules
for both exec code and spec code.
For example, as with exec code, its type must be compilable (e.g. u8, not int),
and, as with spec code, it cannot call any exec or proof functions.
const fn foo() -> u64 { 1 }
const C: u64 = foo(); // FAILS with error "cannot call function `foo` with mode exec"Using an exec const in a spec or proof context
Similar to functions, if you want to use an exec const in a spec or proof context,
you can annotate the declaration with [verifier::when_used_as_spec(SPEC_DEF)],
where SPEC_DEF is the name of a spec const or a spec function with no arguments.
use vstd::layout;
global layout usize is size == 8;
spec const SPEC_USIZE_BYTES: usize = layout::size_of_as_usize::<usize>();
#[verifier::when_used_as_spec(SPEC_USIZE_BYTES)]
exec const USIZE_BYTES: usize
ensures
USIZE_BYTES as nat == layout::size_of::<usize>(),
{
8
}
In this example, without the annotation, Verus will give the error “cannot read const with mode exec.”
Moreover, attempting to use the annotation
#[verifier::when_used_as_spec(layout::size_of::<usize>)],
without defining SPEC_USIZE_BYTES separately,
will also result in an error:
when_used_as_spec can only handle the case when two functions or consts have the same signature.
It doesn’t handle using something like ::<usize> to coerce a function to a different signature.
Trouble-shooting overflow errors
Verus may have difficulty proving that a const declaration does not overflow;
using [verifier::when_used_as_spec(SPEC_DEF)]
or [verifier::non_linear] may help.
For example, here [verifier::non_linear] is added to prevent the error
“possible arithmetic underflow/overflow.”
This allows Verus to reason about the (seemingly)
non-linear expression BAR_PLUS_ONE * BAR,
instead of giving up immediately.
See the chapter on non-linear reasoning for more details.
pub const FOO: u8 = 4;
pub const BAR: u8 = FOO;
pub const BAR_PLUS_ONE: u8 = BAR + 1;
#[verifier::nonlinear]
pub const G: u8 = BAR_PLUS_ONE * BAR;
Putting It All Together
To show how spec, proof, and exec code work together, consider the example
below of computing the n-th triangular number.
We’ll cover this example and the features it uses in more detail in Chapter 4,
so for now, let’s focus on the high-level structure of the code.
We use a spec function triangle to mathematically define our specification using natural numbers (nat)
and a recursive description. We then write a more efficient iterative implementation
as the exec function loop_triangle (recall that exec is the default mode for functions).
We connect the correctness of loop_triangle’s return value to our mathematical specification
in loop_triangle’s ensures clause.
However, to successfully verify loop_triangle, we need a few more things. First, in executable
code, we have to worry about the possibility of arithmetic overflow. To keep things simple here,
we add a precondition to loop_triangle saying that the result needs to be less than one million,
which means it will certainly fit into a u32.
We also need to translate the knowledge that the final triangle result fits in a u32
into the knowledge that each individual step of computing the result won’t overflow,
i.e., that computing sum = sum + idx won’t overflow. We can do this by showing
that triangle is monotonic; i.e., if you increase the argument to triangle, the result increases too.
Showing this property requires an inductive proof. We cover inductive proofs
later; the important thing here is that we can do this proof using a proof function
(triangle_is_monotonic). To invoke the results of our proof in our exec implementation,
we assert that the new sum fits, and as
justification, we an invoke our proof with the relevant arguments. At the
call site, Verus will check that the preconditions for triangle_is_monotonic
hold and then assume that the postconditions hold.
Finally, our implementation uses a while loop, which means it requires some loop invariants, which we cover later.
spec fn triangle(n: nat) -> nat
decreases n,
{
if n == 0 {
0
} else {
n + triangle((n - 1) as nat)
}
}
proof fn triangle_is_monotonic(i: nat, j: nat)
ensures
i <= j ==> triangle(i) <= triangle(j),
decreases j,
{
// We prove the statement `i <= j ==> triangle(i) <= triangle(j)`
// by induction on `j`.
if j == 0 {
// The base case (`j == 0`) is trivial since it's only
// necessary to reason about when `i` and `j` are both 0.
// So no proof lines are needed for this case.
}
else {
// In the induction step, we can assume the statement is true
// for `j - 1`. In Verus, we can get that fact into scope with
// a recursive call substituting `j - 1` for `j`.
triangle_is_monotonic(i, (j - 1) as nat);
// Once we know it's true for `j - 1`, the rest of the proof
// is trivial.
}
}
fn loop_triangle(n: u32) -> (sum: u32)
requires
triangle(n as nat) < 0x1_0000_0000,
ensures
sum == triangle(n as nat),
{
let mut sum: u32 = 0;
let mut idx: u32 = 0;
while idx < n
invariant
idx <= n,
sum == triangle(idx as nat),
triangle(n as nat) < 0x1_0000_0000,
decreases n - idx,
{
idx = idx + 1;
assert(sum + idx < 0x1_0000_0000) by {
triangle_is_monotonic(idx as nat, n as nat);
}
sum = sum + idx;
}
sum
}Recursion and loops
Suppose we want to compute the nth triangular number:
triangle(n) = 0 + 1 + 2 + ... + (n - 1) + n
We can express this as a simple recursive funciton:
spec fn triangle(n: nat) -> nat
decreases n,
{
if n == 0 {
0
} else {
n + triangle((n - 1) as nat)
}
}
This chapter discusses how to define and use recursive functions,
including writing decreases clauses and using fuel.
It then explores a series of verified implementations of triangle,
starting with a basic recursive implementation and ending with a while loop.
Recursive functions, decreases, fuel
Recursive functions are functions that call themselves.
In order to ensure soundness, a recursive spec function must terminate on all inputs —
infinite recursive calls aren’t allowed.
To see why termination is important, consider the following nonterminating function definition:
spec fn bogus(i: int) -> int {
bogus(i) + 1 // FAILS, error due to nontermination
}Verus rejects this definition because the recursive call loops infinitely, never terminating.
If Verus accepted the definion, then you could very easily prove false,
because, for example, the definition insists that bogus(3) == bogus(3) + 1,
which implies that 0 == 1, which is false:
proof fn exploit_bogus()
ensures
false,
{
assert(bogus(3) == bogus(3) + 1);
}To help prove termination,
Verus requires that each recursive spec function definition contain a decreases clause:
spec fn triangle(n: nat) -> nat
decreases n,
{
if n == 0 {
0
} else {
n + triangle((n - 1) as nat)
}
}
Each recursive call must decrease the expression in the decreases clause by at least 1.
Furthermore, the call cannot cause the expression to decrease below 0.
With these restrictions, the expression in the decreases clause serves as an upper bound on the
depth of calls that triangle can make to itself, ensuring termination.
While Verus can often complete these proofs of termination automatically, it sometimes needs additional help with the proof.
Fuel and reasoning about recursive functions
Given the definition of triangle above, we can make some assertions about it:
fn test_triangle_fail() {
assert(triangle(0) == 0); // succeeds
assert(triangle(10) == 55); // FAILS
}The first assertion, about triangle(0), succeeds.
But somewhat surprisingly, the assertion assert(triangle(10) == 55) fails,
despite the fact that triangle(10) really is
equal to 55.
We’ve just encountered a limitation of automated reasoning:
SMT solvers cannot automatically prove all true facts about all recursive functions.
For nonrecursive functions,
an SMT solver can reason about the functions simply by inlining them.
For example, if we have a call min(a + 1, 5) to the min function:
spec fn min(x: int, y: int) -> int {
if x <= y {
x
} else {
y
}
}the SMT solver can replace min(a + 1, 5) with:
if a + 1 <= 5 {
a + 1
} else {
5
}
which eliminates the call. However, this strategy doesn’t completely work with recursive functions, because inlining the function produces another expression with a call to the same function:
triangle(x) = if x == 0 { 0 } else { x + triangle(x - 1) }
Naively, the solver could keep inlining again and again, producing more and more expressions, and this strategy would never terminate:
triangle(x) = if x == 0 { 0 } else { x + triangle(x - 1) }
triangle(x) = if x == 0 { 0 } else { x + (if x - 1 == 0 { 0 } else { x - 1 + triangle(x - 2) }) }
triangle(x) = if x == 0 { 0 } else { x + (if x - 1 == 0 { 0 } else { x - 1 + (if x - 2 == 0 { 0 } else { x - 2 + triangle(x - 3) }) }) }
To avoid this infinite inlining,
Verus limits the number of recursive calls that any given call can spawn in the SMT solver.
This limit is called the fuel;
each nested recursive inlining consumes one unit of fuel.
By default, the fuel is 1, which is just enough for assert(triangle(0) == 0) to succeed
but not enough for assert(triangle(10) == 55) to succeed.
To increase the fuel to a larger amount,
we can use the reveal_with_fuel directive:
fn test_triangle_reveal() {
proof {
reveal_with_fuel(triangle, 11);
}
assert(triangle(10) == 55);
}Here, 11 units of fuel is enough to inline the 11 calls
triangle(0), …, triangle(10).
Note that even if we only wanted to supply 1 unit of fuel,
we could still prove assert(triangle(10) == 55) through a long series of assertions:
fn test_triangle_step_by_step() {
assert(triangle(0) == 0);
assert(triangle(1) == 1);
assert(triangle(2) == 3);
assert(triangle(3) == 6);
assert(triangle(4) == 10);
assert(triangle(5) == 15);
assert(triangle(6) == 21);
assert(triangle(7) == 28);
assert(triangle(8) == 36);
assert(triangle(9) == 45);
assert(triangle(10) == 55); // succeeds
}This works because 1 unit of fuel is enough to prove assert(triangle(0) == 0),
and then once we know that triangle(0) == 0,
we only need to inline triangle(1) once to get:
triangle(1) = if 1 == 0 { 0 } else { 1 + triangle(0) }
Now the SMT solver can use the previously computed triangle(0) to simplify this to:
triangle(1) = if 1 == 0 { 0 } else { 1 + 0 }
and then produce triangle(1) == 1.
Likewise, the SMT solver can then use 1 unit of fuel to rewrite triangle(2)
in terms of triangle(1), proving triangle(2) == 3, and so on.
However, it’s probably best to avoid long series of assertions if you can,
and instead write a proof that makes it clear why the SMT proof fails by default
(not enough fuel) and fixes exactly that problem:
fn test_triangle_assert_by() {
assert(triangle(10) == 55) by {
reveal_with_fuel(triangle, 11);
}
}Recursive exec and proof functions, proofs by induction
The previous section introduced a specification for triangle numbers. Given that, let’s try a series of executable implementations of triangle numbers, starting with a simple recursive implementation:
fn rec_triangle(n: u32) -> (sum: u32)
ensures
sum == triangle(n as nat),
{
if n == 0 {
0
} else {
n + rec_triangle(n - 1) // FAILS: possible overflow
}
}We immediately run into one small practical difficulty: the implementation needs to use a finite-width integer to hold the result, and this integer may overflow:
error: possible arithmetic underflow/overflow
|
| n + rec_triangle(n - 1) // FAILS: possible overflow
| ^^^^^^^^^^^^^^^^^^^^^^^
Indeed, we can’t expect the implementation to work if the result
won’t fit in the finite-width integer type,
so it makes sense to add a precondition saying
that the result must fit,
which for a u32 result means triangle(n) < 0x1_0000_0000:
fn rec_triangle(n: u32) -> (sum: u32)
requires
triangle(n as nat) < 0x1_0000_0000,
ensures
sum == triangle(n as nat),
decreases n,
{
if n == 0 {
0
} else {
n + rec_triangle(n - 1)
}
}This time, verification succeeds.
It’s worth pausing for a few minutes, though, to understand why the verification succeeds.
For example, an execution of rec_triangle(10)
performs 10 separate additions, each of which could potentially overflow.
How does Verus know that none of these 10 additions will overflow,
given just the initial precondition triangle(10) < 0x1_0000_0000?
The answer is that each instance of triangle(n) for n != 0
makes a recursive call to triangle(n - 1),
and this recursive call must satisfy the precondition triangle(n - 1) < 0x1_0000_0000.
Let’s look at how this is proved.
If we know triangle(n) < 0x1_0000_0000 from rec_triangle’s precondition
and we use 1 unit of fuel to inline the definition of triangle once,
we get:
triangle(n) < 0x1_0000_0000
triangle(n) = if n == 0 { 0 } else { n + triangle(n - 1) }
In the case where n != 0, this simplifies to:
triangle(n) < 0x1_0000_0000
triangle(n) = n + triangle(n - 1)
From this, we conclude n + triangle(n - 1) < 0x1_0000_0000,
which means that triangle(n - 1) < 0x1_0000_0000,
since 0 <= n, since n has type u32, which is nonnegative.
Intuitively, you can imagine that as rec_triangle executes,
proofs about triangle(n) < 0x1_0000_0000 gets passed down the stack to the recursive calls,
proving triangle(10) < 0x1_0000_0000 in the first call,
then triangle(9) < 0x1_0000_0000 in the second call,
triangle(8) < 0x1_0000_0000 in the third call,
and so on.
(Of course, the proofs don’t actually exist at run-time —
they are purely static and are erased before compilation —
but this is still a reasonable way to think about it.)
Towards an imperative implementation: mutation and tail recursion
The recursive implementation presented above is easy to write and verify,
but it’s not very efficient, since it requires a lot of stack space for the recursion.
Let’s take a couple small steps towards a more efficient, imperative implementation
based on while loops.
First, to prepare for the mutable variables that we’ll use in while loops,
let’s switch sum from being a return value to being a mutably updated variable:
fn mut_triangle(n: u32, sum: &mut u32)
requires
triangle(n as nat) < 0x1_0000_0000,
ensures
*sum == triangle(n as nat),
decreases n,
{
if n == 0 {
*sum = 0;
} else {
mut_triangle(n - 1, sum);
*sum = *sum + n;
}
}From the verification’s point of view, this doesn’t change anything significant.
Internally, when performing verification,
Verus simply represents the final value of *sum as a return value,
making the verification of mut_triangle essentially the same as
the verification of rec_triangle.
Next, let’s try to eliminate the excessive stack usage by making the function
tail recursive.
We do this by introducing an index variable idx that counts up from 0 to n,
just as a while loop would do:
fn tail_triangle(n: u32, idx: u32, sum: &mut u32)
requires
idx <= n,
*old(sum) == triangle(idx as nat),
triangle(n as nat) < 0x1_0000_0000,
ensures
*sum == triangle(n as nat),
{
if idx < n {
let idx = idx + 1;
*sum = *sum + idx;
tail_triangle(n, idx, sum);
}
}In the preconditions and postconditions,
the expression *old(sum) refers to the initial value of *sum,
at the entry to the function,
while *sum refers to the final value, at the exit from the function.
The precondition *old(sum) == triangle(idx as nat) specifies that
as tail_triangle executes more and more recursive calls,
sum accumulates the sum 0 + 1 + ... + idx.
Each recursive call increases idx by 1 until idx reaches n,
at which point sum equals 0 + 1 + ... + n and the function simply returns sum unmodified.
When we try to verify tail_triangle, though, Verus reports an error about possible overflow:
error: possible arithmetic underflow/overflow
|
| *sum = *sum + idx;
| ^^^^^^^^^^
This may seem perplexing at first:
why doesn’t the precondition triangle(n as nat) < 0x1_0000_0000
automatically take care of the overflow,
as it did for rec_triangle and mut_triangle?
The problem is that we’ve reversed the order of the addition and the recursive call.
rec_triangle and mut_triangle made the recursive call first,
and then performed the addition.
This allowed them to prove all the necessary
facts about overflow first in the series of recursive calls
(e.g. proving triangle(10) < 0x1_0000_0000, triangle(9) < 0x1_0000_0000,
…, triangle(0) < 0x1_0000_0000)
before doing the arithmetic that depends on these facts.
But tail_triangle tries to perform the arithmetic first,
before the recursion,
so it never has a chance to develop these facts from the original
triangle(n) < 0x1_0000_0000 assumption.
Proofs by induction
In the example of computing triangle(10),
we need to know triangle(0) < 0x1_0000_0000,
then triangle(1) < 0x1_0000_0000,
and so on, but we only know triangle(10) < 0x1_0000_0000 to start with.
If we somehow knew that
triangle(0) <= triangle(10),
triangle(1) <= triangle(10),
and so on,
then we could derive what we want from triangle(10) < 0x1_0000_0000.
What we need is a lemma that proves that if i <= j,
then triangle(i) <= triangle(j).
In other words, we need to prove that triangle is monotonic.
We can use a proof function to implement this lemma:
proof fn triangle_is_monotonic(i: nat, j: nat)
ensures
i <= j ==> triangle(i) <= triangle(j),
decreases j,
{
// We prove the statement `i <= j ==> triangle(i) <= triangle(j)`
// by induction on `j`.
if j == 0 {
// The base case (`j == 0`) is trivial since it's only
// necessary to reason about when `i` and `j` are both 0.
// So no proof lines are needed for this case.
}
else {
// In the induction step, we can assume the statement is true
// for `j - 1`. In Verus, we can get that fact into scope with
// a recursive call substituting `j - 1` for `j`.
triangle_is_monotonic(i, (j - 1) as nat);
// Once we know it's true for `j - 1`, the rest of the proof
// is trivial.
}
}
The proof is by induction on j,
where the base case of the induction is i == j
and the induction step relates j - 1 to j.
In Verus, the induction step is implemented as a recursive call from the proof to itself
(in this example, this recursive call is line triangle_is_monotonic(i, (j - 1) as nat)).
As with recursive spec functions,
recursive proof functions must terminate and need a decreases clause.
Otherwise, it would be easy to prove false,
as in the following non-terminating “proof”:
proof fn circular_reasoning()
ensures
false,
{
circular_reasoning(); // FAILS, does not terminate
}We can use the triangle_is_monotonic lemma to complete the verification of tail_triangle:
fn tail_triangle(n: u32, idx: u32, sum: &mut u32)
requires
idx <= n,
*old(sum) == triangle(idx as nat),
triangle(n as nat) < 0x1_0000_0000,
ensures
*sum == triangle(n as nat),
decreases n - idx,
{
if idx < n {
let idx = idx + 1;
assert(*sum + idx < 0x1_0000_0000) by {
triangle_is_monotonic(idx as nat, n as nat);
}
*sum = *sum + idx;
tail_triangle(n, idx, sum);
}
}Intuitively, we can think of the call from tail_triangle to triangle_is_monotonic
as performing a similar recursive proof that rec_triangle and mut_triangle
performed as they proved their triangle(n) < 0x1_0000_0000 preconditions
in their recursive calls.
In going from rec_triangle and mut_triangle to tail_triangle,
we’ve just shifted this recursive reasoning from the executable code into a separate recursive lemma.
Lightweight termination checking
While recursive spec functions and proof functions must always terminate and therefore must always contain a decreases clause, nontermination is allowed for exec functions. Nevertheless, by default, Verus still requires that recursive exec functions and loops in exec mode have a decreases clause. This only guarantees that the present function will terminate, on the assumption that all the callees also terminate so it should be treated as a lint, not a complete guarantee of termination.
The attribute #![verifier::exec_allows_no_decreases_clause] can be used to disable this check for a function, module, or crate.
Loops and invariants
The previous section developed a tail-recursive implementation of triangle:
fn tail_triangle(n: u32, idx: u32, sum: &mut u32)
requires
idx <= n,
*old(sum) == triangle(idx as nat),
triangle(n as nat) < 0x1_0000_0000,
ensures
*sum == triangle(n as nat),
decreases n - idx,
{
if idx < n {
let idx = idx + 1;
assert(*sum + idx < 0x1_0000_0000) by {
triangle_is_monotonic(idx as nat, n as nat);
}
*sum = *sum + idx;
tail_triangle(n, idx, sum);
}
}We can rewrite this as a while loop as follows:
fn loop_triangle(n: u32) -> (sum: u32)
requires
triangle(n as nat) < 0x1_0000_0000,
ensures
sum == triangle(n as nat),
{
let mut sum: u32 = 0;
let mut idx: u32 = 0;
while idx < n
invariant
idx <= n,
sum == triangle(idx as nat),
triangle(n as nat) < 0x1_0000_0000,
decreases n - idx,
{
idx = idx + 1;
assert(sum + idx < 0x1_0000_0000) by {
triangle_is_monotonic(idx as nat, n as nat);
}
sum = sum + idx;
}
sum
}The loop is quite similar to the tail-recursive implementation.
(In fact, internally, Verus verifies the loop as if it were its own function,
separate from the enclosing loop_triangle function.)
Where the tail-recursive function had preconditions,
the loop has loop invariants that describe what must
be true before and after each iteration of the loop.
For example, if n = 10,
then the loop invariant must be true 11 times:
before each of the 10 iterations,
and after the final iteration.
Notice that the invariant idx <= n allows for the possibility that idx == n,
since this will be the case after the final iteration.
If we tried to write the invariant as idx < n,
then Verus would fail to prove that the invariant is maintained after the final iteration.
After the loop exits,
Verus knows that idx <= n (because of the loop invariant)
and it knows that the loop condition idx < n must have been false
(otherwise, the loop would have continued).
Putting these together allows Verus to prove that idx == n after exiting the loop.
Since we also have the invariant sum == triangle(idx as nat),
Verus can then substitute n for idx to conclude sum == triangle(n as nat),
which proves the postcondition of loop_triangle.
Just as verifying functions requires some programmer effort to write
appropriate preconditions and postconditions,
verifying loops requires programmer effort to write loop invariants.
The loop invariants have to be neither too weak (invariant true is usually too weak)
nor too strong (invariant false is too strong),
so that:
- the invariants hold upon the initial entry to the loop
(e.g.
idx <= nholds for the initial valueidx = 0, since0 <= n) - the invariant still holds at the end of the loop body, so that the invariant is maintained across loop iterations
- the invariant is strong enough to prove the properties we want
to know after the loop exits (e.g. to prove
loop_triangle’s postcondition)
As mentioned above,
Verus verifies the loop separately from the function that contains the loop
(e.g. separately from loop_triangle).
This means that the loop does not automatically inherit preconditions
like triangle(n as nat) < 0x1_0000_0000 from the surrounding function —
if the loop relies on these preconditions,
they must be listed explicitly in the loop invariants.
(The reason for this is to improve the efficiency of the SMT solving
for large functions with large while loops;
verification runs faster if Verus breaks the surrounding function and the loops into separate pieces
and verifies them modularly.)
Verus does allow you to opt-out of this behavior, meaning that your loops will inherit
information from the surrounding context. This will simplify your loop invariants,
but verification time may increase for medium-to-large functions.
To opt-out for a single function or while loop, you can add the attribute
#[verifier::loop_isolation(false)]. You can also opt-out at the module or
crate level, by adding the #![verifier::loop_isolation(false)] attribute
to the module or the root of the crate. You can then override the global
setting locally by adding #[verifier::loop_isolation(true)] on individual
functions or loops.
Loops with break
Loops can exit early using return or break.
Suppose, for example, we want to remove the requirement
triangle(n as nat) < 0x1_0000_0000 from the loop_triangle function,
and instead check for overflow at run-time.
The following version of the function uses return to return
the special value 0xffff_ffff in case overflow is detected at run-time:
fn loop_triangle_return(n: u32) -> (sum: u32)
ensures
sum == triangle(n as nat) || (sum == 0xffff_ffff && triangle(n as nat) >= 0x1_0000_0000),
{
let mut sum: u32 = 0;
let mut idx: u32 = 0;
while idx < n
invariant
idx <= n,
sum == triangle(idx as nat),
decreases n - idx,
{
idx = idx + 1;
if sum as u64 + idx as u64 >= 0x1_0000_0000 {
proof {
triangle_is_monotonic(idx as nat, n as nat);
}
return 0xffff_ffff;
}
sum = sum + idx;
}
sum
}Another way to exit early from a loop is with a break inside the loop body.
However, break complicates the specification of a loop slightly.
For simple while loops without a break,
Verus knows that the loop condition (e.g. idx < n)
must be false after exiting the loop.
If there is a break, though, the loop condition is not necessarily false
after the loop, because the break might cause the loop to exit even when
the loop condition is true.
To deal with this, while loops with a break,
as well as Rust loop expressions (loops with no condition),
must explicitly specify what is true after the loop exit using ensures clauses,
as shown in the following code.
Furthermore, invariants that don’t hold after a break
must be marked as invariant_except_break rather than invariant:
fn loop_triangle_break(n: u32) -> (sum: u32)
ensures
sum == triangle(n as nat) || (sum == 0xffff_ffff && triangle(n as nat) >= 0x1_0000_0000),
{
let mut sum: u32 = 0;
let mut idx: u32 = 0;
while idx < n
invariant_except_break
idx <= n,
sum == triangle(idx as nat),
ensures
sum == triangle(n as nat) || (sum == 0xffff_ffff && triangle(n as nat) >= 0x1_0000_0000),
decreases n - idx,
{
idx = idx + 1;
if sum as u64 + idx as u64 >= 0x1_0000_0000 {
proof {
triangle_is_monotonic(idx as nat, n as nat);
}
sum = 0xffff_ffff;
break;
}
sum = sum + idx;
}
sum
}For Loops
The previous section introduced a while loop implementation of triangle:
fn loop_triangle(n: u32) -> (sum: u32)
requires
triangle(n as nat) < 0x1_0000_0000,
ensures
sum == triangle(n as nat),
{
let mut sum: u32 = 0;
let mut idx: u32 = 0;
while idx < n
invariant
idx <= n,
sum == triangle(idx as nat),
triangle(n as nat) < 0x1_0000_0000,
decreases n - idx,
{
idx = idx + 1;
assert(sum + idx < 0x1_0000_0000) by {
triangle_is_monotonic(idx as nat, n as nat);
}
sum = sum + idx;
}
sum
}We can rewrite this as a for loop as follows:
fn for_loop_triangle(n: u32) -> (sum: u32)
requires
triangle(n as nat) < 0x1_0000_0000,
ensures
sum == triangle(n as nat),
{
let mut sum: u32 = 0;
for idx in iter: 0..n
invariant
sum == triangle(idx as nat),
triangle(n as nat) < 0x1_0000_0000,
{
assert(sum + idx + 1 < 0x1_0000_0000) by {
triangle_is_monotonic((idx + 1) as nat, n as nat);
}
sum = sum + idx + 1;
}
sum
}The only difference between this for loop and the while loop
is that idx is automatically incremented by 1 at the end of the
each iteration.
In addition, iter.start, iter.cur, iter.end reveal the start, current, and end
for the iterator of range 0..n.
iter@ records all the elements that the iterator has iterated so far.
In the above example, if idx=3, iter@ =~= seq![0,1,2]
Lexicographic decreases clauses
For some recursive functions,
it’s difficult to specify a single value that decreases
in each recursive call.
For example, the Ackermann function
has two parameters m and n,
and neither m nor n decrease in all 3 of the recursive calls:
spec fn ackermann(m: nat, n: nat) -> nat
decreases m, n,
{
if m == 0 {
n + 1
} else if n == 0 {
ackermann((m - 1) as nat, 1)
} else {
ackermann((m - 1) as nat, ackermann(m, (n - 1) as nat))
}
}
proof fn test_ackermann() {
reveal_with_fuel(ackermann, 9);
assert(ackermann(2, 3) == 9);
}For this situation, Verus allows the decreases clause to contain multiple expressions,
and it treats these expressions as
lexicographically ordered.
For example, decreases m, n means that one of the following must be true:
- m stays the same, and n decreases,
which happens in the call
ackermann(m, (n - 1) as nat) - m decreases and n may increase or decrease arbitrarily,
which happens in the two calls of the form
ackermann((m - 1) as nat, ...)
Mutual recursion
Functions may be mutually recursive,
as in the following example where is_even calls is_odd recursively
and is_odd calls is_even recursively:
spec fn abs(i: int) -> int {
if i < 0 {
-i
} else {
i
}
}
spec fn is_even(i: int) -> bool
decreases abs(i),
{
if i == 0 {
true
} else if i > 0 {
is_odd(i - 1)
} else {
is_odd(i + 1)
}
}
spec fn is_odd(i: int) -> bool
decreases abs(i),
{
if i == 0 {
false
} else if i > 0 {
is_even(i - 1)
} else {
is_even(i + 1)
}
}
proof fn even_odd_mod2(i: int)
ensures
is_even(i) <==> i % 2 == 0,
is_odd(i) <==> i % 2 == 1,
decreases abs(i),
{
if i < 0 {
even_odd_mod2(i + 1);
}
if i > 0 {
even_odd_mod2(i - 1);
}
}
fn test_even() {
proof {
reveal_with_fuel(is_even, 11);
}
assert(is_even(10));
}
fn test_odd() {
proof {
reveal_with_fuel(is_odd, 11);
}
assert(!is_odd(10));
}The recursion here works for both positive and negative i;
in both cases, the recursion decreases abs(i), the absolute value of i.
An alternate way to write this mutual recursion is:
spec fn is_even(i: int) -> bool
decreases abs(i), 0int,
{
if i == 0 {
true
} else if i > 0 {
is_odd(i - 1)
} else {
is_odd(i + 1)
}
}
spec fn is_odd(i: int) -> bool
decreases abs(i), 1int,
{
!is_even(i)
}
proof fn even_odd_mod2(i: int)
ensures
is_even(i) <==> i % 2 == 0,
is_odd(i) <==> i % 2 == 1,
decreases abs(i),
{
reveal_with_fuel(is_odd, 2);
if i < 0 {
even_odd_mod2(i + 1);
}
if i > 0 {
even_odd_mod2(i - 1);
}
}
fn test_even() {
proof {
reveal_with_fuel(is_even, 21);
}
assert(is_even(10));
}
fn test_odd() {
proof {
reveal_with_fuel(is_odd, 22);
}
assert(!is_odd(10));
}In this alternate version, the recursive call !is_even(i) doesn’t
decrease abs(i), so we can’t just use abs(i) as the decreases clause by itself.
However, we can employ a trick with lexicographic ordering.
If we write decreases abs(i), 1,
then the call to !is_even(i) keeps the first expression abs(i) the same,
but decreases the second expression from 1 to 0,
which satisfies the lexicographic requirements for decreasing.
The call is_odd(i - 1) also obeys lexicographic ordering,
since it decreases the first expression abs(i),
which allows the second expression to increase from 0 to 1.
Datatypes: Structs and Enums
Datatypes, in both executable code and specifications, are
defined via Rust’s struct and enum.
Struct
Struct
In Verus, just as in Rust, you can use struct to define a datatype that
collects a set of fields together:
struct Point {
x: int,
y: int,
}Spec and exec code can refer to struct fields:
impl Point {
spec fn len2(&self) -> int {
self.x * self.x + self.y * self.y
}
}
fn rotate_90(p: Point) -> (o: Point)
ensures o.len2() == p.len2()
{
let o = Point { x: -p.y, y: p.x };
assert((-p.y) * (-p.y) == p.y * p.y) by(nonlinear_arith);
o
}Enum
Enum
In Verus, just as in Rust, you can use enum to define a datatype that is any one of the
defined variants:
enum Beverage {
Coffee { creamers: nat, sugar: bool },
Soda { flavor: Syrup },
Water { ice: bool },
}An enum is often used just for its tags, without member fields:
enum Syrup {
Cola,
RootBeer,
Orange,
LemonLime,
}Identifying a variant with the is operator
In spec contexts, the is operator lets you query which variant of an
enum a variable contains.
fn make_float(bev: Beverage) -> Dessert
requires bev is Soda
{
assert(bev !is Coffee);
Dessert::new(/*...*/)
}The syntax !is is a shorthand for !(.. is ..).
Accessing fields with the arrow operator
If all the fields have distinct names, as in the Beverage example,
you can refer to fields with the arrow -> operator:
proof fn sufficiently_creamy(bev: Beverage) -> bool
requires bev is Coffee
{
bev->creamers >= 2
}If an enum field reuses a name, you can qualify the field access:
enum Life {
Mammal { legs: int, has_pocket: bool },
Arthropod { legs: int, wings: int },
Plant { leaves: int },
}
spec fn is_insect(l: Life) -> bool
{
l is Arthropod && l->Arthropod_legs == 6
}match works as in Rust.
enum Shape {
Circle(int),
Rect(int, int),
}
spec fn area_2(s: Shape) -> int {
match s {
Shape::Circle(radius) => { radius * radius * 3 },
Shape::Rect(width, height) => { width * height }
}
}For variants like Shape declared with round parentheses (),
you can use Verus’ `->’ tuple-like syntax to access a single field
without a match destruction:
spec fn rect_height(s: Shape) -> int
recommends s is Rect
{
s->1
}matches with &&, ==>, and &&&
match is natural for examining every variant of an enum.
If you’d like to bind the fields while only considering one or two of the
variants, you can use Verus’ matches syntax:
use Life::*;
spec fn cuddly(l: Life) -> bool {
||| l matches Mammal { legs, .. } && legs == 4
||| l matches Arthropod { legs, wings } && legs == 8 && wings == 0
}Because the matches syntax binds names in patterns, it has no trouble
with field names reused across variants, so it may be preferable
to the (qualified) arrow syntax.
Notice that l matches Mammal{legs} && legs == 4 is a boolean expression,
with the special property that legs is bound in the remainder of the
expression after &&. That helpful binding also works with ==>
and &&&:
spec fn is_kangaroo(l: Life) -> bool {
&&& l matches Life::Mammal { legs, has_pocket }
&&& legs == 2
&&& has_pocket
}
spec fn walks_upright(l: Life) -> bool {
l matches Life::Mammal { legs, .. } ==> legs == 2
}Libraries
The Verus standard library, vstd, comes with a variety of utilities and
datatypes for proofs, as well as runtime functionality with specifications.
Most Verus programs will start with use vstd::prelude::*;, which pulls
in a default set of definitions that we find generally useful. This chapter
will introduce a few of them, but you can find more complete descriptions
in the vstd documentation.
Specification libraries: Seq, Set, Map
The Verus libraries contain types Seq<T>, Set<T>, and Map<Key, Value>
for representing sequences, sets, and maps in specifications.
In contrast to executable Rust collection datatypes in
std::collections,
the Seq, Set and Map types
represent collections of arbitrary size.
For example, while the len() method of
std::collections::HashSet
returns a length of type usize,
which is bounded,
the len() methods of Seq and Set return
lengths of type nat, which is unbounded.
Furthermore, Set and Map can represent infinite sets and maps.
(Sequences, on the other hand, are always finite.)
This allows specifications to talk about collections that
are larger than could be contained in the physical memory of a computer.
Constructing and using Seq, Set, Map
The seq!, set!, and map! macros construct values of type Seq, Set, and Map
with particular contents:
proof fn test_seq1() {
let s: Seq<int> = seq![0, 10, 20, 30, 40];
assert(s.len() == 5);
assert(s[2] == 20);
assert(s[3] == 30);
}
proof fn test_set1() {
let s: Set<int> = set![0, 10, 20, 30, 40];
assert(s.finite());
assert(s.contains(20));
assert(s.contains(30));
assert(!s.contains(60));
}
proof fn test_map1() {
let m: Map<int, int> = map![0 => 0, 10 => 100, 20 => 200, 30 => 300, 40 => 400];
assert(m.dom().contains(20));
assert(m.dom().contains(30));
assert(!m.dom().contains(60));
assert(m[20] == 200);
assert(m[30] == 300);
}
The macros above can only construct finite sequences, sets, and maps.
There are also functions Seq::new, Set::new, and Map::new,
which can allocate both finite values and (for sets and maps) infinite values:
proof fn test_seq2() {
let s: Seq<int> = Seq::new(5, |i: int| 10 * i);
assert(s.len() == 5);
assert(s[2] == 20);
assert(s[3] == 30);
}
proof fn test_set2() {
let s: Set<int> = Set::new(|i: int| 0 <= i <= 40 && i % 10 == 0);
assert(s.contains(20));
assert(s.contains(30));
assert(!s.contains(60));
let s_infinite: Set<int> = Set::new(|i: int| i % 10 == 0);
assert(s_infinite.contains(20));
assert(s_infinite.contains(30));
assert(!s_infinite.contains(35));
}
proof fn test_map2() {
let m: Map<int, int> = Map::new(|i: int| 0 <= i <= 40 && i % 10 == 0, |i: int| 10 * i);
assert(m[20] == 200);
assert(m[30] == 300);
let m_infinite: Map<int, int> = Map::new(|i: int| i % 10 == 0, |i: int| 10 * i);
assert(m_infinite[20] == 200);
assert(m_infinite[30] == 300);
assert(m_infinite[90] == 900);
}Each Map<Key, Value> value has a domain of type Set<Key> given by .dom().
In the test_map2 example above, m’s domain is the finite set {0, 10, 20, 30, 40},
while m_infinite’s domain is the infinite set {..., -20, 10, 0, 10, 20, ...}.
For more operations, including sequence contenation (.add or +),
sequence update,
sequence subrange,
set union (.union or +),
set intersection (.intersect),
etc.,
see:
See also the API documentation.
Proving properties of Seq, Set, Map
The SMT solver will prove some properties about Seq, Set, and Map automatically, as shown in the examples above. However, some other properties may require calling lemmas in the library or may require proofs by induction.
If two collections (Seq, Set, or Map) have the same elements,
Verus considers them to be equal.
This is known as equality via extensionality.
However, the SMT solver will in general not automatically recognize that
the two collections are equal
if the collections were constructed in different ways.
For example, the following 3 sequences are equal,
but calling check_eq fails:
proof fn check_eq(x: Seq<int>, y: Seq<int>)
requires
x == y,
{
}
proof fn test_eq_fail() {
let s1: Seq<int> = seq![0, 10, 20, 30, 40];
let s2: Seq<int> = seq![0, 10] + seq![20] + seq![30, 40];
let s3: Seq<int> = Seq::new(5, |i: int| 10 * i);
check_eq(s1, s2); // FAILS, even though s1 equals s2
check_eq(s1, s3); // FAILS, even though s1 equals s3
}To convince the SMT solver that s1, s2, and s3 are equal,
we have to explicitly assert the equality via the extensional equality operator =~=,
rather than just the ordinary equality operator ==.
Using =~= forces the SMT solver
to check that all the elements of the collections are equal,
which it would not ordinarily do, so that the following succeeds:
proof fn check_eq_extensionally(x: Seq<int>, y: Seq<int>)
requires
x =~= y,
{
}
proof fn test_eq() {
let s1: Seq<int> = seq![0, 10, 20, 30, 40];
let s2: Seq<int> = seq![0, 10] + seq![20] + seq![30, 40];
let s3: Seq<int> = Seq::new(5, |i: int| 10 * i);
check_eq_extensionally(s1, s2); // succeeds
check_eq_extensionally(s1, s3); // succeeds
}We can use assert(s1 =~= s2), for example, to prove that s1 equals s2
before calling the original check_eq:
proof fn check_eq(x: Seq<int>, y: Seq<int>)
requires
x == y,
{
}
proof fn test_eq2() {
let s1: Seq<int> = seq![0, 10, 20, 30, 40];
let s2: Seq<int> = seq![0, 10] + seq![20] + seq![30, 40];
let s3: Seq<int> = Seq::new(5, |i: int| 10 * i);
assert(s1 =~= s2);
assert(s1 =~= s3);
check_eq(s1, s2); // succeeds
check_eq(s1, s3); // succeeds
}(Note that by default, Verus will automatically promote == to =~=
inside assert, ensures, and invariant,
so that, for example, assert(s1 == s2) actually means assert(s1 =~= s2).
See the Equality via extensionality section for more details.)
Proofs about set cardinality (Set::len) and set finiteness (Set::finite)
often require inductive proofs.
For example, the exact cardinality of the intersection of two sets
depends on which elements the two sets have in common.
If the two sets are disjoint,
the intersection’s cardinality will be 0,
but otherwise, the intersections’s cardinality will be some non-zero value.
Let’s try to prove that the intersection’s cardinality is no larger than
either of the two sets’ cardinalities.
Without loss of generality, we can just prove that
the intersection’s cardinality is no larger than the first set’s cardinality:
s1.intersect(s2).len() <= s1.len().
The proof (which is found in set_lib.rs)
is by induction on the size of the set s1.
In the induction step, we need to make s1 smaller,
which means we need to remove an element from it.
The two methods .choose and .remove allow us to choose
an arbitrary element from s1 and remove it:
let a = s1.choose();
... s1.remove(a) ...Based on this, we expect an inductive proof to look something like the following,
where the inductive step removes s1.choose():
pub proof fn lemma_len_intersect<A>(s1: Set<A>, s2: Set<A>)
requires
s1.finite(),
ensures
s1.intersect(s2).len() <= s1.len(),
decreases
s1.len(),
{
if s1.is_empty() {
} else {
let a = s1.choose();
lemma_len_intersect(s1.remove(a), s2);
}
}Unfortunately, Verus fails to verify this proof. Therefore, we’ll need to fill in the base case and induction case with some more detail. Before adding this detail to the code, let’s think about what a fully explicit proof might look like if we wrote it out by hand:
pub proof fn lemma_len_intersect<A>(s1: Set<A>, s2: Set<A>)
requires
s1.finite(),
ensures
s1.intersect(s2).len() <= s1.len(),
decreases
s1.len(),
{
if s1.is_empty() {
// s1 is the empty set.
// Therefore, s1.intersect(s2) is also empty.
// So both s1.len() and s1.intersect(s2).len() are 0,
// and 0 <= 0.
} else {
// s1 is not empty, so it has at least one element.
// Let a be an element from s1.
// Let s1' be the set s1 with the element a removed (i.e. s1' == s1 - {a}).
// Removing an element decreases the cardinality by 1, so s1'.len() == s1.len() - 1.
// By induction, s1'.intersect(s2).len() <= s1'.len(), so:
// (s1 - {a}).intersect(s2).len() <= s1'.len()
// (s1.intersect(s2) - {a}).len() <= s1'.len()
// (s1.intersect(s2) - {a}).len() <= s1.len() - 1
// case a in s1.intersect(s2):
// (s1.intersect(s2) - {a}).len() == s1.intersect(s2).len() - 1
// case a not in s1.intersect(s2):
// (s1.intersect(s2) - {a}).len() == s1.intersect(s2).len()
// In either case:
// s1.intersect(s2).len() <= (s1.intersect(s2) - {a}).len() + 1
// Putting all the inequalities together:
// s1.intersect(s2).len() <= (s1.intersect(s2) - {a}).len() + 1 <= (s1.len() - 1) + 1
// So:
// s1.intersect(s2).len() <= (s1.len() - 1) + 1
// s1.intersect(s2).len() <= s1.len()
}
}For such a simple property, this is a surprisingly long proof! Fortunately, the SMT solver can automatically prove most of the steps written above. What it will not automatically prove, though, is any step requiring equality via extensionality, as discussed earlier. The two crucial steps requiring equality via extensionality are:
- “Therefore, s1.intersect(s2) is also empty.”
- Replacing
(s1 - {a}).intersect(s2)withs1.intersect(s2) - {a}
For these, we need to explicitly invoke =~=:
pub proof fn lemma_len_intersect<A>(s1: Set<A>, s2: Set<A>)
requires
s1.finite(),
ensures
s1.intersect(s2).len() <= s1.len(),
decreases
s1.len(),
{
if s1.is_empty() {
assert(s1.intersect(s2) =~= s1);
} else {
let a = s1.choose();
assert(s1.intersect(s2).remove(a) =~= s1.remove(a).intersect(s2));
lemma_len_intersect(s1.remove(a), s2);
}
}With this, Verus and the SMT solver successfully complete the proof.
However, Verus and the SMT solver aren’t the only audience for this proof.
Anyone maintaining this code might want to know why we invoked =~=,
and we probably shouldn’t force them to work out the entire hand-written proof above
to rediscover this.
So although it’s not strictly necessary,
it’s probably polite to wrap the assertions in assert...by to indicate
the purpose of the =~=:
pub proof fn lemma_len_intersect<A>(s1: Set<A>, s2: Set<A>)
requires
s1.finite(),
ensures
s1.intersect(s2).len() <= s1.len(),
decreases s1.len(),
{
if s1.is_empty() {
assert(s1.intersect(s2).len() == 0) by {
assert(s1.intersect(s2) =~= s1);
}
} else {
let a = s1.choose();
lemma_len_intersect(s1.remove(a), s2);
// by induction: s1.remove(a).intersect(s2).len() <= s1.remove(a).len()
assert(s1.intersect(s2).remove(a).len() <= s1.remove(a).len()) by {
assert(s1.intersect(s2).remove(a) =~= s1.remove(a).intersect(s2));
}
// simplifying ".remove(a).len()" yields s1.intersect(s2).len() <= s1.len())
}
}Executable libraries: Vec
The previous section discussed the mathematical collection types
Seq, Set, and Map.
This section will discuss Vec, an executable implementation of Seq.
Verus supports some functionality of Rust’s std::vec::Vec type. To use
Vec, include use std::vec::Vec; in your code.
You can allocate Vec using Vec::new and then push elements into it:
fn test_vec1() {
let mut v: Vec<u32> = Vec::new();
v.push(0);
v.push(10);
v.push(20);
v.push(30);
v.push(40);
assert(v.len() == 5);
assert(v[2] == 20);
assert(v[3] == 30);
v.set(2, 21);
assert(v[2] == 21);
assert(v[3] == 30);
}The code above is able to make assertions directly about the Vec value v.
You could also write more compilicated specifications and proofs about Vec values.
In general, though, Verus encourages programmers to write spec functions
and proof functions about mathematical types like Seq, Set, and Map instead
of hard-wiring the specifications and proofs to particular concrete datatypes like Vec.
This allows spec functions and proof functions to focus on the essential ideas,
written in terms of mathematical types like Seq, Set, Map, int, and nat,
rather than having to fiddle around with finite-width integers like usize,
worry about arithmetic overflow, etc.
Of course, there needs to be a connection between the mathematical types
and the concrete types, and specifications in exec functions will commonly have to move
back and forth between mathematical abstractions and concrete reality.
To make this easier, Verus supports the syntactic sugar @ for extracting
a mathematical view from a concrete type.
For example, v@ returns a Seq of all the elements in the vector v:
spec fn has_five_sorted_numbers(s: Seq<u32>) -> bool {
s.len() == 5 && s[0] <= s[1] <= s[2] <= s[3] <= s[4]
}
fn test_vec2() {
let mut v: Vec<u32> = Vec::new();
v.push(0);
v.push(10);
v.push(20);
v.push(30);
v.push(40);
v.set(2, 21);
assert(v@ =~= seq![0, 10, 21, 30, 40]);
assert(v@ =~= seq![0, 10] + seq![21] + seq![30, 40]);
assert(v@[2] == 21);
assert(v@[3] == 30);
assert(v@.subrange(2, 4) =~= seq![21, 30]);
assert(has_five_sorted_numbers(v@));
}Using the Seq view of the Vec allows us to use the various features of Seq,
such as concatenation and subsequences,
when writing specifications about the Vec contents.
Verus support for std::vec::Vec is currently being expanded. For up-to-date
documentation, visit this link.
Note that these functions provide specifications for std::vec::Vec functions. Thus,
for example, ex_vec_insert represents support for the Vec function insert. Code written
in Verus should use insert rather than ex_vec_insert.
Documentation for std::vec::Vec functionality can be found here.
Spec Closures
Verus supports anonymous functions (known as “closures” in Rust) in ghost code.
For example, the following code from earlier in this chapter
uses an anonymous function |i: int| 10 * i
to initialize a sequence with the values 0, 10, 20, 30, 40:
proof fn test_seq2() {
let s: Seq<int> = Seq::new(5, |i: int| 10 * i);
assert(s.len() == 5);
assert(s[2] == 20);
assert(s[3] == 30);
}The anonymous function |i: int| 10 * i has type spec_fn(int) -> int
and has mode spec.
Because it has mode spec,
the anonymous function is subject to the same restrictions as named spec functions.
(For example, it can call other spec functions but not proof functions or exec functions.)
Note that in contrast to standard executable
Rust closures,
where Fn, FnOnce, and FnMut are traits,
spec_fn(int) -> int is a type, not a trait.
Therefore, ghost code can return a spec closure directly,
using a return value of type spec_fn(t1, ..., tn) -> tret,
without having to use
dyn or impl,
as with standard executable Rust closures.
For example, the spec function adder, shown below,
can return an anonymous function that adds x to y:
spec fn adder(x: int) -> spec_fn(int) -> int {
|y: int| x + y
}
proof fn test_adder() {
let f = adder(10);
assert(f(20) == 30);
assert(f(60) == 70);
}Developing Proofs
In this chapter, we present several examples showing useful techniques for developing proofs about your code in Verus.
Using assert and assume to develop proofs
In an earlier chapter, we started with an outline of a proof:
pub proof fn lemma_len_intersect<A>(s1: Set<A>, s2: Set<A>)
requires
s1.finite(),
ensures
s1.intersect(s2).len() <= s1.len(),
decreases
s1.len(),
{
if s1.is_empty() {
} else {
let a = s1.choose();
lemma_len_intersect(s1.remove(a), s2);
}
}and then filled in the crucial missing steps to complete the proof. It didn’t say, though, how you might go about discovering which crucial steps are missing. In practice, it takes some experimentation to fill in this kind of proof.
This section will walk through a typical process of developing a proof,
using the proof outline above as a starting point.
The process will consist of a series of queries to Verus and the SMT solver,
using assert and assume to ask questions,
and using the answers to narrow in on the cause of the verification failure.
If we run the proof above, Verus reports an error:
error: postcondition not satisfied
|
| s1.intersect(s2).len() <= s1.len(),
| ---------------------------------- failed this postcondition
This raises a couple questions:
- Why is this postcondition failing?
- If this postcondition succeeded, would the verification of the whole function succeed?
Let’s check the second question first. We can simply assume the postcondition and see what happens:
pub proof fn lemma_len_intersect<A>(s1: Set<A>, s2: Set<A>)
...
{
if s1.is_empty() {
} else {
let a = s1.choose();
lemma_len_intersect::<A>(s1.remove(a), s2);
}
assume(s1.intersect(s2).len() <= s1.len());
}In this case, verification succeeds:
verification results:: verified: 1 errors: 0
There are two paths through the code, one when s1.is_empty() and one when !s1.empty().
The failure could lie along either path, or both.
Let’s prepare to work on each branch of the if/else separately
by moving a separate copy of the assume into each branch:
{
if s1.is_empty() {
assume(s1.intersect(s2).len() <= s1.len());
} else {
let a = s1.choose();
lemma_len_intersect::<A>(s1.remove(a), s2);
assume(s1.intersect(s2).len() <= s1.len());
}
}verification results:: verified: 1 errors: 0
Next, let’s change the first assume to an assert to see if it succeeds in the if branch:
{
if s1.is_empty() {
assert(s1.intersect(s2).len() <= s1.len());
} else {
let a = s1.choose();
lemma_len_intersect::<A>(s1.remove(a), s2);
assume(s1.intersect(s2).len() <= s1.len());
}
}error: assertion failed
|
| assert(s1.intersect(s2).len() <= s1.len());
| ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ assertion failed
In the s1.is_empty() case, we expect s1.len() == 0 (an empty set has cardinality 0).
We can double-check this with a quick assertion:
{
if s1.is_empty() {
assert(s1.len() == 0);
assume(s1.intersect(s2).len() <= s1.len());
} else {
...
}
}verification results:: verified: 1 errors: 0
So what we need is s1.intersect(s2).len() <= 0.
If this were true, we’d satisfy the postcondition here:
{
if s1.is_empty() {
assume(s1.intersect(s2).len() <= 0);
assert(s1.intersect(s2).len() <= s1.len());
} else {
...
}
}verification results:: verified: 1 errors: 0
Since set cardinality is a nat, the only way it can be <= 0 is if it’s equal to 0:
{
if s1.is_empty() {
assume(s1.intersect(s2).len() == 0);
assert(s1.intersect(s2).len() <= s1.len());
} else {
...
}
}verification results:: verified: 1 errors: 0
and the only way it can be 0 is if the set is the empty set:
{
if s1.is_empty() {
assume(s1.intersect(s2) == Set::<A>::empty());
assert(s1.intersect(s2).len() == 0);
assert(s1.intersect(s2).len() <= s1.len());
} else {
...
}
}verification results:: verified: 1 errors: 0
So we’ve narrowed in on the problem:
the intersection of the empty set s1 with another set should equal the empty set,
but the verifier doesn’t see this automatically.
And from the previous section’s discussion of equality, we can guess why:
the SMT solver doesn’t always automatically prove equalities between collections,
but instead requires us to assert the equality using extensionality.
So we can add the extensionality assertion:
{
if s1.is_empty() {
assert(s1.intersect(s2) =~= Set::<A>::empty());
assert(s1.intersect(s2).len() == 0);
assert(s1.intersect(s2).len() <= s1.len());
} else {
...
}
}verification results:: verified: 1 errors: 0
It works! We’ve now verified the s1.is_empty() case,
and we can turn our attention to the !s1.is_empty() case:
{
if s1.is_empty() {
...
} else {
let a = s1.choose();
lemma_len_intersect::<A>(s1.remove(a), s2);
assume(s1.intersect(s2).len() <= s1.len());
}
}Changing this assume to an assert fails,
so we’ve got work to do in this case as well:
{
if s1.is_empty() {
...
} else {
let a = s1.choose();
lemma_len_intersect::<A>(s1.remove(a), s2);
assert(s1.intersect(s2).len() <= s1.len());
}
}error: assertion failed
|
| assert(s1.intersect(s2).len() <= s1.len());
| ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ assertion failed
Fortunately, the recursive call lemma_len_intersect::<A>(s1.remove(a), s2) succeeded,
so we have some information from the postcondition of this call.
Let’s write this out explictly so we can examine it more closely,
substituting s1.remove(a) for s1:
{
if s1.is_empty() {
...
} else {
let a = s1.choose();
lemma_len_intersect::<A>(s1.remove(a), s2);
assert(s1.remove(a).intersect(s2).len() <= s1.remove(a).len());
assume(s1.intersect(s2).len() <= s1.len());
}
}verification results:: verified: 1 errors: 0
Let’s compare what we know above s1.remove(a) with what we’re trying to prove about s1:
assert(s1.remove(a).intersect(s2).len() <= s1.remove(a).len()); // WE KNOW THIS
assume(s1 .intersect(s2).len() <= s1 .len()); // WE WANT THISIs there any way we can make what we know look more like what we want?
For example, how does s1.remove(a).len() relate to s1.len()?
The value a is an element of s1, so if we remove it from s1,
it should decrease the cardinality by 1:
{
if s1.is_empty() {
...
} else {
let a = s1.choose();
lemma_len_intersect::<A>(s1.remove(a), s2);
assert(s1.remove(a).intersect(s2).len() <= s1.remove(a).len());
assert(s1.remove(a).len() == s1.len() - 1);
assume(s1.intersect(s2).len() <= s1.len());
}
}verification results:: verified: 1 errors: 0
So we can simplify a bit:
{
if s1.is_empty() {
...
} else {
let a = s1.choose();
lemma_len_intersect::<A>(s1.remove(a), s2);
assert(s1.remove(a).intersect(s2).len() <= s1.remove(a).len());
assert(s1.remove(a).intersect(s2).len() <= s1.len() - 1);
assert(s1.remove(a).intersect(s2).len() + 1 <= s1.len());
assume(s1.intersect(s2).len() <= s1.len());
}
}verification results:: verified: 1 errors: 0
Now the missing piece is the relation between s1.remove(a).intersect(s2).len() + 1
and s1.intersect(s2).len():
{
if s1.is_empty() {
...
} else {
let a = s1.choose();
lemma_len_intersect::<A>(s1.remove(a), s2);
assert(s1.remove(a).intersect(s2).len() <= s1.remove(a).len());
assert(s1.remove(a).intersect(s2).len() <= s1.len() - 1);
assert(s1.remove(a).intersect(s2).len() + 1 <= s1.len());
assume(s1.intersect(s2).len() <= s1.remove(a).intersect(s2).len() + 1);
assert(s1.intersect(s2).len() <= s1.len());
}
}verification results:: verified: 1 errors: 0
If we can prove the assumption s1.intersect(s2).len() <= s1.remove(a).intersect(s2).len() + 1,
we’ll be done:
assume(s1 .intersect(s2).len()
<= s1.remove(a).intersect(s2).len() + 1);Is there anyway we can make s1.remove(a).intersect(s2) look more like s1.intersect(s2)
so that it’s easier to prove this inequality?
If we switched the order from s1.remove(a).intersect(s2) to s1.intersect(s2).remove(a),
then the subexpression s1.intersect(s2) would match:
assume(s1.intersect(s2) .len()
<= s1.intersect(s2).remove(a).len() + 1);so let’s try that:
{
if s1.is_empty() {
...
} else {
let a = s1.choose();
lemma_len_intersect::<A>(s1.remove(a), s2);
assert(s1.remove(a).intersect(s2).len() <= s1.remove(a).len());
assert(s1.remove(a).intersect(s2).len() <= s1.len() - 1);
assert(s1.remove(a).intersect(s2).len() + 1 <= s1.len());
assert(s1.intersect(s2).len() <= s1.intersect(s2).remove(a).len() + 1);
assert(s1.intersect(s2).len() <= s1.remove(a).intersect(s2).len() + 1);
assert(s1.intersect(s2).len() <= s1.len());
}
}error: assertion failed
|
| assert(s1.intersect(s2).len() <= s1.remove(a).intersect(s2).len() + 1);
| ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ assertion failed
One of these assertion succeeds and the other fails.
The only difference between the successful assertion
and the failing assertion is the order of intersect and remove
in s1.intersect(s2).remove(a) and s1.remove(a).intersect(s2),
so all we need to finish the proof is for s1.intersect(s2).remove(a)
to be equal to s1.remove(a).intersect(s2):
{
if s1.is_empty() {
...
} else {
let a = s1.choose();
lemma_len_intersect::<A>(s1.remove(a), s2);
assert(s1.remove(a).intersect(s2).len() <= s1.remove(a).len());
assert(s1.remove(a).intersect(s2).len() <= s1.len() - 1);
assert(s1.remove(a).intersect(s2).len() + 1 <= s1.len());
assert(s1.intersect(s2).len() <= s1.intersect(s2).remove(a).len() + 1);
assume(s1.intersect(s2).remove(a) == s1.remove(a).intersect(s2));
assert(s1.intersect(s2).len() <= s1.remove(a).intersect(s2).len() + 1);
assert(s1.intersect(s2).len() <= s1.len());
}
}verification results:: verified: 1 errors: 0
Again, we found ourselves needing to know the equality of two collections. And again, the first thing to try is to assert extensional equality:
{
if s1.is_empty() {
...
} else {
let a = s1.choose();
lemma_len_intersect::<A>(s1.remove(a), s2);
assert(s1.remove(a).intersect(s2).len() <= s1.remove(a).len());
assert(s1.remove(a).intersect(s2).len() <= s1.len() - 1);
assert(s1.remove(a).intersect(s2).len() + 1 <= s1.len());
assert(s1.intersect(s2).len() <= s1.intersect(s2).remove(a).len() + 1);
assert(s1.intersect(s2).remove(a) =~= s1.remove(a).intersect(s2));
assert(s1.intersect(s2).len() <= s1.remove(a).intersect(s2).len() + 1);
assert(s1.intersect(s2).len() <= s1.len());
}
}verification results:: verified: 1 errors: 0
It works!
Now we’ve eliminated all the assumes, so we’ve completed the verification:
pub proof fn lemma_len_intersect<A>(s1: Set<A>, s2: Set<A>)
requires
s1.finite(),
ensures
s1.intersect(s2).len() <= s1.len(),
decreases
s1.len(),
{
if s1.is_empty() {
assert(s1.intersect(s2) =~= Set::empty());
assert(s1.intersect(s2).len() == 0);
assert(s1.intersect(s2).len() <= s1.len());
} else {
let a = s1.choose();
lemma_len_intersect::<A>(s1.remove(a), s2);
assert(s1.remove(a).intersect(s2).len() <= s1.remove(a).len());
assert(s1.remove(a).intersect(s2).len() <= s1.len() - 1);
assert(s1.remove(a).intersect(s2).len() + 1 <= s1.len());
assert(s1.intersect(s2).len() <= s1.intersect(s2).remove(a).len() + 1);
assert(s1.intersect(s2).remove(a) =~= s1.remove(a).intersect(s2));
assert(s1.intersect(s2).len() <= s1.remove(a).intersect(s2).len() + 1);
assert(s1.intersect(s2).len() <= s1.len());
}
}verification results:: verified: 1 errors: 0
The code above contains a lot of unnecessary asserts, though,
so it’s worth spending a few minutes cleaning the code up
for sake of anyone who has to maintain the code in the future.
We want to clear out unnecessary code so there’s less code to maintain,
but keep enough information so
someone maintaining the code can still understand the code.
The right amount of information is a matter of taste,
but we can try to strike a reasonable balance between conciseness and informativeness:
pub proof fn lemma_len_intersect<A>(s1: Set<A>, s2: Set<A>)
requires
s1.finite(),
ensures
s1.intersect(s2).len() <= s1.len(),
decreases s1.len(),
{
if s1.is_empty() {
assert(s1.intersect(s2).len() == 0) by {
assert(s1.intersect(s2) =~= s1);
}
} else {
let a = s1.choose();
lemma_len_intersect(s1.remove(a), s2);
// by induction: s1.remove(a).intersect(s2).len() <= s1.remove(a).len()
assert(s1.intersect(s2).remove(a).len() <= s1.remove(a).len()) by {
assert(s1.intersect(s2).remove(a) =~= s1.remove(a).intersect(s2));
}
// simplifying ".remove(a).len()" yields s1.intersect(s2).len() <= s1.len())
}
}Devising Loop Invariants
Below, we develop several examples that show how to work through the process of devising invariants for loops.
Example 1: Fibonacci
Suppose our goal is to compute values in the Fibonacci sequence.
We use a spec function fib to mathematically define our specification using nats
and a recursive description:
spec fn fib(n: nat) -> nat
decreases n,
{
if n == 0 {
0
} else if n == 1 {
1
} else {
fib((n - 2) as nat) + fib((n - 1) as nat)
}
}Our goal is to write a more efficient iterative implementation as the exec
function fib_impl. To keep things simple, we’ll add a precondition to
fib_impl saying that the result needs to fit into a u64 value.
We connect the correctness of fib_impl’s return value
to our mathematical specification in fib_impl’s ensures clause.
fn fib_impl(n: u64) -> (result: u64)
requires
fib(n as nat) <= u64::MAX
ensures
result == fib(n as nat),
{
if n == 0 {
return 0;
}
let mut prev: u64 = 0;
let mut cur: u64 = 1;
let mut i: u64 = 1;
while i < n
{
i = i + 1;
let new_cur = cur + prev;
prev = cur;
cur = new_cur;
}
cur
}However, if we ask Verus to verify this code, it reports two errors:
error: postcondition not satisfied
|
| result == fib(n as nat),
| ----------------------- failed this postcondition
and
error: possible arithmetic underflow/overflow
|
| let new_cur = cur + prev;
| ^^^^^^^^^^
Let’s start by addressing the first failure. It shouldn’t be surprising that Verus
can’t tell that we satisfy the postcondition, since our while loop doesn’t have any
invariants. This means that after the while loop terminates, Verus doesn’t know
anything about what happened inside the loop, except that the loop’s conditional (i < n)
no longer holds. To fix this, let’s try to craft an invariant that summarizes the work
we’re doing inside the loop that we think will lead to satisfying the postcondition.
In this case, since we return cur and expect it to be fib(n as nat), let’s add
the invariant that cur == fib(i as nat).
If we run Verus, we see that this still isn’t enough to satisfy the
postcondition. Why? Let’s think about what Verus knows after the loop
terminates. It knows our invariant, and it knows !(i < n), which is
equivalent to i >= n. When we think about it this way, it’s clear what the
problem is: Verus doesn’t know that i == n! Hence, we need another invariant
to relate i and n as the loop progresses. We know i starts at 1, and it
should end at n, so let’s add the invariant 1 <= i <= n. Notice that we
need to use i <= n, since in the last iteration of the loop, we will start
with i == n - 1 and then increment i, and an invariant must always be
true after the loop body executes.
With this new invariant, Verus no longer reports an error about the
postcondition, so we’ve made progress! To be explicit about the progress we’ve
made, after the loop terminates, Verus now knows (thanks to our new invariant)
that i <= n, and from the fact that the loop terminates, it also knows that
i >= n, so it can conclude that i == n, and hence from the invariant that
cur == fib(i as nat), it now knows that cur == fib(n as nat).
Unfortunately, Verus is still concerned about arithmetic underflow/overflow,
and it also reports a new error, saying that our new invariant about cur
doesn’t hold. Let’s tackle the underflow/overflow issue first. Note that we can
deduce that the problem is a potential overflow, since we’re adding two
non-negative numbers. We also know from our precondition that fib(n as nat) will fit into a u64, but to use this information inside the while loop,
we need to add it as an invariant too. See the earlier discussion of loops
and invariants for why this is the case. This still isn’t enough,
however. We also need to know something about the value of prev if we want
to show that cur + prev will not overflow. Since we’re using prev to track
earlier values of Fibonacci, let’s add prev == fib((i - 1) as nat) as an
invariant.
Despite these new invariants, Verus still reports the same error. Why? The issue
is that although we know that fib(n as nat) won’t overflow, that doesn’t necessarily
mean that fib(i as nat) won’t overflow. As humans, we know this is true, because
i < n and fib is monotonic (i.e., it always grows larger as its argument increases).
Proving this property, however, requires an inductive proof. Before writing
the proof itself, let’s just state the property we want as a lemma and see if
it suffices to make our proof go through. Here’s the Verus version of the
informal property we want. We write it as a proof mode function, since its
only purpose is to establish this property.
proof fn lemma_fib_is_monotonic(i: nat, j: nat)
requires
i <= j,
ensures
fib(i) <= fib(j),
{
}Verus can’t yet prove this, but let’s try invoking it in our while loop.
To call this lemma in our exec implementation, we employ
a proof {} block and pass in the relevant arguments. At the call site, Verus checks
that the preconditions for lemma_fib_is_monotonic hold and then assumes that the postconditions hold.
fn fib_impl(n: u64) -> (result: u64)
requires
fib(n as nat) <= u64::MAX
ensures
result == fib(n as nat),
{
if n == 0 {
return 0;
}
let mut prev: u64 = 0;
let mut cur: u64 = 1;
let mut i: u64 = 1;
while i < n
invariant
0 < i <= n,
fib(n as nat) <= u64::MAX,
cur == fib(i as nat),
prev == fib((i - 1) as nat),
decreases n - i,
{
i = i + 1;
proof {
lemma_fib_is_monotonic(i as nat, n as nat);
}
let new_cur = cur + prev;
prev = cur;
cur = new_cur;
}
cur
}We put the lemma invocation after the increment of i, so that it establishes that
fib(i as nat) <= fib(n as nat) for the new value of i that we’re about to compute
by summing cur and prev. With this lemma invocation, fib_impl now verifies!
We’re not done yet, however. We still need to prove lemma_fib_is_monotonic. To
construct our inductive proof, we need to lay out the base cases, and then help
Verus with the inductive step(s). Here’s the basic skeleton:
proof fn lemma_fib_is_monotonic(i: nat, j: nat)
requires
i <= j,
ensures
fib(i) <= fib(j),
{
if j < 2 {
} else if i == j {
} else if i == j - 1 {
} else {
assume(false);
}
}Notice that we’ve added assume(false) to the final tricky case (following the approach
of using assert and assume to build our proof). When we run
Verus, it succeeds, indicating that Verus doesn’t need any help with our base cases.
The final portion of the proof, however, needs more help (you can confirm this by
by removing the assume(false) and observing that the proof fails).
The key idea here is to use our induction hypothesis to show that fib(i)
is smaller than both fib(j - 1) and fib(j - 2). We do this via two recursive invocations
of lemma_fib_is_monotonic. Note that adding recursive calls means we need to add a decreases clause.
In this case, we’re decreasing the distance between j and i, so j - i works.
proof fn lemma_fib_is_monotonic(i: nat, j: nat)
requires
i <= j,
ensures
fib(i) <= fib(j),
decreases j - i,
{
if j < 2 {
} else if i == j {
} else if i == j - 1 {
} else {
lemma_fib_is_monotonic(i, (j - 1) as nat);
lemma_fib_is_monotonic(i, (j - 2) as nat);
}
}With these additions, the proof succeeds, meaning that our entire program now verifies successfully!
Example 2: Account Balance
In this example, we’re given a slice of i64 values that represent a series of deposits and
withdrawals from a bank account. The goal is to determine whether the account’s balance ever
drops below 0. We formalize this requirement with the spec function always_non_negative,
which is itself defined in terms of computing a sum of the first i elements in a sequence of i64 values.
spec fn always_non_negative(s: Seq<i64>) -> bool
{
forall|i: int| 0 <= i <= s.len() ==> sum(#[trigger] s.take(i)) >= 0
}
spec fn sum(s: Seq<i64>) -> int
decreases s.len(),
{
if s.len() == 0 {
0
} else {
sum(s.drop_last()) + s.last()
}
}In our implementation, as usual, we tie the concrete result r to our spec
in the ensures clause.
fn non_negative(operations: &[i64]) -> (r: bool)
ensures
r == always_non_negative(operations@),
{
let mut s = 0i128;
for i in 0usize..operations.len()
{
s = s + operations[i] as i128;
if s < 0 {
return false;
}
}
true
}Note that we use an i128 to compute the account’s running
sum since it allows us to have sufficiently large numbers without overflowing.
As an exercise, you can try modifying the implementation to use an i64 for
the sum instead, adding any additional invariants and proofs you need.
Here we use a for loop instead of a while loop, which means that we get a free
invariant that 0 <= i <= operations.len(). As before, however, that’s not
enough to prove our postcondition or even to rule out overflow; Verus reports:
error: postcondition not satisfied
|
| r == always_non_negative(operations@),
| ------------------------------------- failed this postcondition
| / {
| | let mut s = 0i128;
| | for i in 0usize..operations.len()
| | {
... |
| | true
| | }
| |_^ at the end of the function body
error: possible arithmetic underflow/overflow
|
| s = s + operations[i] as i128;
| ^^^^^^^^^^^^^^^^^^^^^^^^^
Let’s address the possible underflow/overflow first. Why don’t we expect this to happen?
Well, we don’t expect underflow because we start with s = 0, and if at any point s goes
below 0, we immediately return. How far can s go below 0? At worst, we might subtract i64::MIN
from 0, so we can argue that i64::MIN <= s is an invariant. To rule out overflow, we need
to consider how large s can grow. A simple bound is to say that if we add i i64 values
together, the sum must be bounded by i64::MAX * i. Putting this together, we can add a loop
invariant that says i64::MIN <= s <= i64::MAX * i. With this invariant in place, Verus no
longer complains about possible arithmetic underflow/overflow.
Now let’s address functional correctness, so that we can prove the postcondition holds. As before,
we want our loop invariants to summarize the progress that we’ve made towards the postcondition,
ideally in a form such that when the loop terminates, the invariant nicely matches up with the
expression in the postcondition. A first step in this direction is to make it explicit that s
represents the sum of the values up to i; i.e., s == sum(operations@.take(i as int)). We
also need to keep track of the fact that we’ve checked each individual sum to confirm that it’s non-negative.
In other words, we need forall|j: int| 0 <= j <= i ==> sum(#[trigger] operations@.take(j)) >= 0.
With these additions, Verus produces new complaints:
error: invariant not satisfied at end of loop body
|
| s == sum(operations@.take(i as int)),
| ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
error: postcondition not satisfied
|
| r == always_non_negative(operations@),
| ------------------------------------- failed this postcondition
...
| return false;
| ^^^^^^^^^^^^ at this exitAre these two different issues or two symptoms of the same underlying issue? One way to check this is by assuming that the first one is true and seeing what happens to the second error. In other words, we update the body of the loop to be:
s = s + operations[i] as i128;
assume(s == sum(operations@.take((i + 1) as int)));
if s < 0 {
return false;
}It turns out this assumption eliminates both errors, so we really only need to convince Verus that
we’ve correctly computed the sum of the first i+1 operations. If we let ops_i_plus_1 be operations@.take((i + 1) as int) and unfold the definition of sum,
we can see that sum(ops_i_plus_1) == sum(ops_i_plus_1.drop_last()) + ops_i_plus_1.last().
This means Verus is having trouble determining that the right-hand side matches the value we computed
(namely s + operations[i]). Lets check that the second term in the two sums match, namely:
assert(operations[i as int] == ops_i_plus_1.last());That succeeds, so the problem must be showing that s
(which we know from our invariant is sum(operations@.take(i as int))) is equal to sum(ops_i_plus_1.drop_last()).
Clearly, these two values would be equal if the arguments to sum were equal, so let’s see if Verus can prove that,
which we can check by writing:
assert(operations@.take(i as int) == ops_i_plus_1.drop_last());Verus is able to verify this assertion, and not only that, it can then prove our previous assumption that
s == sum(operations@.take((i + 1) as int), hence completing our proof. Why does this work? Stating the
assertion causes Verus to invoke axioms about sequence extensionality, i.e., the conditions
under which two sequences are equal, which then allows it to prove our sequences are equal, which proves
the sums are equal, which completes the proof.
Here’s the full version of the verifying implementation.
fn non_negative(operations: &[i64]) -> (r: bool)
ensures
r == always_non_negative(operations@),
{
let mut s = 0i128;
for i in 0usize..operations.len()
invariant
s == sum(operations@.take(i as int)),
forall|j: int| 0 <= j <= i ==> sum(#[trigger] operations@.take(j)) >= 0,
i64::MIN <= s <= i64::MAX * i,
{
assert(operations@.take(i as int) =~= operations@.take(
(i + 1) as int,
).drop_last());
s = s + operations[i] as i128;
if s < 0 {
return false;
}
}
true
}Proving Absence of Overflow
Whenever Verus executable code performs a mathematical operation on
concrete (non-ghost) variables, Verus makes sure that it doesn’t overflow.
This is useful because it prevents unexpected overflow (a common bug) and
because it allows simpler reasoning, e.g., not forcing the SMT solver to
reason about the possibility that x + y results in (x + y) % pow(2, 32). However, it creates an obligation on the developer to prove that
every one of their operations can’t overflow. We saw in the previous
section about Devising loop invariants that this
necessitates additional proof work.
One way to deal with this is to place explicit bounds on variables’ values so that the solver can infer that the code can’t overflow. For instance, the following simple function to compute a sum fails to verify because it might overflow:
fn compute_sum_fails(x: u64, y: u64) -> (result: u64)
ensures
result == x + y,
{
x + y // error: possible arithmetic underflow/overflow
}But this version succeeds at verification because the solver can easily tell that the bounds prevent overflow:
fn compute_sum_limited(x: u64, y: u64) -> (result: u64)
requires
x < 1000000,
y < 1000000,
ensures
result == x + y,
{
x + y
}Another way to deal with overflow is to explicitly check for it at
runtime. For this, one can use operations from the Rust standard library
like checked_add and checked_mul. These operations return an Option,
with the value None indicating that an overflow would have resulted.
Verus includes specifications for these, enabling their direct use.
This example illustrates how:
fn compute_sum_runtime_check(x: u64, y: u64) -> (result: Option<u64>)
ensures
match result {
Some(z) => z == x + y,
None => x + y > u64::MAX,
},
{
x.checked_add(y)
}
fn main() {
}
} // verus!
This works well for single operations, but performing multiple chained
operations of addition and/or multiplication is trickier. This is because
whenever overflow occurs one has to stop, and it’s not clear that the
entire chain of operations collectively would have overflowed. For this
circumstance, the Verus standard library includes structs named
CheckedU8, CheckedU16, etc. Each of these can continue operating even
after it overflows, maintaining its true non-overflowing value in ghost
state. To see the value in this, consider the Fibonacci example from the
previous section about Devising loop invariants. If we use
CheckedU64, as in the following example, we don’t need to invoke
lemma_fib_is_monotonic to prove that the result can’t overflow:
fn fib_checked(n: u64) -> (result: u64)
requires
fib(n as nat) <= u64::MAX
ensures
result == fib(n as nat),
{
if n == 0 {
return 0;
}
let mut prev: CheckedU64 = CheckedU64::new(0);
let mut cur: CheckedU64 = CheckedU64::new(1);
let mut i: u64 = 1;
while i < n
invariant
0 < i <= n,
fib(n as nat) <= u64::MAX,
cur@ == fib(i as nat),
prev@ == fib((i - 1) as nat),
decreases n - i,
{
i = i + 1;
let new_cur = cur.add_checked(&prev);
prev = cur;
cur = new_cur;
}
cur.unwrap()
}There is a small cost in performance and memory footprint, since the
checked versions consist of a runtime Option<u64> instead of a u64, but
in return the code is simpler. Another advantage is that we can remove the
precondition mandating that the result must fit in a u64, and correctly
handle the possibility of overflow:
fn fib_checked_no_precondition(n: u64) -> (result: Option<u64>)
ensures
match result {
Some(x) => x == fib(n as nat),
None => fib(n as nat) > u64::MAX,
},
{
if n == 0 {
return Some(0);
}
let mut prev: CheckedU64 = CheckedU64::new(0);
let mut cur: CheckedU64 = CheckedU64::new(1);
let mut i: u64 = 1;
while i < n
invariant
0 < i <= n,
cur@ == fib(i as nat),
prev@ == fib((i - 1) as nat),
decreases n - i,
{
i = i + 1;
let new_cur = cur.add_checked(&prev);
prev = cur;
cur = new_cur;
}
cur.to_option()
}Quantifiers
Suppose that we want to specify that all the elements of a sequence are even. If the sequence has a small, fixed size, we could write a specification for every element separately:
spec fn is_even(i: int) -> bool {
i % 2 == 0
}
proof fn test_seq_5_is_evens(s: Seq<int>)
requires
s.len() == 5,
is_even(s[0]),
is_even(s[1]),
is_even(s[3]),
is_even(s[3]),
is_even(s[4]),
{
assert(is_even(s[3]));
}Clearly, though, this won’t scale well to larger sequences or sequences of unknown length.
We could write a recursive specification:
spec fn all_evens(s: Seq<int>) -> bool
decreases s.len(),
{
if s.len() == 0 {
true
} else {
is_even(s.last()) && all_evens(s.drop_last())
}
}
proof fn test_seq_recursive(s: Seq<int>)
requires
s.len() == 5,
all_evens(s),
{
assert(is_even(s[3])) by {
reveal_with_fuel(all_evens, 2);
}
}However, using a recursive definition will lead to many proofs by induction, which can require a lot of programmer effort to write.
Fortunately, Verus and SMT solvers support the
universal and existential quantifiers
forall and exists,
which we can think of as infinite conjunctions or disjunctions:
(forall|i: int| f(i)) = ... f(-2) && f(-1) && f(0) && f(1) && f(2) && ...
(exists|i: int| f(i)) = ... f(-2) || f(-1) || f(0) || f(1) || f(2) || ...
With this, it’s much more convenient to write a specification about all elements of a sequence:
proof fn test_use_forall(s: Seq<int>)
requires
5 <= s.len(),
forall|i: int| 0 <= i < s.len() ==> #[trigger] is_even(s[i]),
{
assert(is_even(s[3]));
}Although quantifiers are very powerful, they require some care, because the SMT solver’s reasoning about quantifiers is incomplete. This isn’t a deficiency in the SMT solver’s implementation, but rather a deeper issue: it’s an undecidable problem to figure out whether a formula with quantifiers, functions, and arithmetic is valid or not, so there’s no complete algorithm that the SMT solver could implement. Instead, the SMT solver uses an incomplete strategy based on triggers, which instantiates quantifiers when expressions match trigger patterns.
This chapter will describe how to use forall and exists,
how triggers work,
and some related topics on choose expressions and closures.
forall and triggers
Let’s take a closer look at the following code,
which uses a forall expression in a requires clause
to prove an assertion:
proof fn test_use_forall(s: Seq<int>)
requires
5 <= s.len(),
forall|i: int| 0 <= i < s.len() ==> #[trigger] is_even(s[i]),
{
assert(is_even(s[3]));
}The forall expression means that 0 <= i < s.len() ==> is_even(s[i])
for all possible integers i:
...
0 <= -3 < s.len() ==> is_even(s[-3])
0 <= -2 < s.len() ==> is_even(s[-2])
0 <= -1 < s.len() ==> is_even(s[-1])
0 <= 0 < s.len() ==> is_even(s[0])
0 <= 1 < s.len() ==> is_even(s[1])
0 <= 2 < s.len() ==> is_even(s[2])
0 <= 3 < s.len() ==> is_even(s[3])
...
There are infinitely many integers i, so the list shown above is infinitely long.
We can’t expect the SMT solver to literally expand the forall into
an infinite list of expressions.
Furthermore, in this example, we only care about one of the expressions,
the expression for i = 3,
since this is all we need to prove assert(is_even(s[3])):
0 <= 3 < s.len() ==> is_even(s[3])Ideally, the SMT solver will choose just the i that are likely to be relevant
to verifying a particular program.
The most common technique that SMT solvers use for choosing likely relevant i
is based on triggers
(also known as SMT patterns or just
patterns).
A trigger is simply an expression or set of expressions that the SMT solver uses as a pattern
to match with.
In the example above, the #[trigger] attribute marks the expression is_even(s[i])
as the trigger for the forall expression.
Based on this attribute,
the SMT solver looks for expressions of the form is_even(s[...]).
During the verification of the test_use_forall function shown above,
there is one expression that has this form: is_even(s[3]).
This matches the trigger is_even(s[i]) exactly for i = 3.
Based on this pattern match, the SMT solver chooses i = 3 and introduces the following fact:
0 <= 3 < s.len() ==> is_even(s[3])This fact allows the SMT solver to complete the proof about the assertion
assert(is_even(s[3])).
Triggers are the way you program the instantiations of the forall expressions
(and the way you program proofs of exists expressions, as discussed in a later section).
By choosing different triggers, you can influence how the forall expressions
get instantiated with different values, such as i = 3 in the example above.
Suppose, for example, we change the assertion slightly so that we assert
s[3] % 2 == 0 instead of is_even(s[3]).
Mathematically, these are both equivalent.
However, the assertion about s[3] % 2 == 0 fails:
spec fn is_even(i: int) -> bool {
i % 2 == 0
}
proof fn test_use_forall_fail(s: Seq<int>)
requires
5 <= s.len(),
forall|i: int| 0 <= i < s.len() ==> #[trigger] is_even(s[i]),
{
assert(s[3] % 2 == 0); // FAILS: doesn't trigger is_even(s[i])
}This fails because there are no expressions matching the pattern is_even(s[...]);
the expression s[3] % 2 == 0 doesn’t mention is_even at all.
In order to prove s[3] % 2 == 0,
we’d first have to mention is_even(s[3]) explicitly:
proof fn test_use_forall_succeeds1(s: Seq<int>)
requires
5 <= s.len(),
forall|i: int| 0 <= i < s.len() ==> #[trigger] is_even(s[i]),
{
assert(is_even(s[3])); // triggers is_even(s[3])
assert(s[3] % 2 == 0); // succeeds, because previous line already instantiated the forall
}Once the expression is_even(s[3]) coaxes the SMT solver into instantiating the
forall expression with i = 3,
the SMT solver can use the resulting 0 <= 3 < s.len() ==> is_even(s[3])
to prove s[3] % 2 == 0.
Alternatively, we could just choose a trigger that is less picky.
For example, the trigger s[i] matches any expression of the form
s[...], which includes the s[3] inside s[3] % 2 == 0 and
also includes the s[3] inside is_even(s[3]):
proof fn test_use_forall_succeeds2(s: Seq<int>)
requires
5 <= s.len(),
forall|i: int| 0 <= i < s.len() ==> is_even(#[trigger] s[i]),
{
assert(s[3] % 2 == 0); // succeeds by triggering s[3]
}In fact, if we omit the #[trigger] attribute entirely,
Verus chooses the trigger s[i] automatically:
proof fn test_use_forall_succeeds3(s: Seq<int>)
requires
5 <= s.len(),
forall|i: int| 0 <= i < s.len() ==> is_even(s[i]), // Verus chooses s[i] as the trigger and prints a note
{
assert(s[3] % 2 == 0); // succeeds by triggering s[3]
}In fact, Verus prints a note stating that it chose this trigger:
note: automatically chose triggers for this expression:
|
| forall|i: int| 0 <= i < s.len() ==> is_even(s[i]), // Verus chooses s[i] as the trigger
| ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
note: trigger 1 of 1:
|
| forall|i: int| 0 <= i < s.len() ==> is_even(s[i]), // Verus chooses s[i] as the trigger
| ^^^^
note: Verus printed one or more automatically chosen quantifier triggers
because it had low confidence in the chosen triggers.
Verus isn’t sure, though,
whether the programmer wants s[i] as the trigger or is_even(s[i]) as the trigger.
It slightly prefers s[i] because s[i] is smaller than is_even(s[i]),
so it chooses s[i],
but it also prints out the note encouraging the programmer to review the decision.
The programmer can accept this decision by writing #![auto] before the quantifier body,
which suppresses the note:
proof fn test_use_forall_succeeds4(s: Seq<int>)
requires
5 <= s.len(),
forall|i: int|
#![auto]
0 <= i < s.len() ==> is_even(s[i]), // Verus chooses s[i] as the trigger
{
assert(s[3] % 2 == 0); // succeeds by triggering s[3]
}Valid triggers and invalid triggers
In practice, a valid trigger needs to follow two rules:
- A trigger for a statement needs to contain all of its non-free variables, meaning those variables that are instantiated by a forall or an exist. In order to achieve this, you can split the trigger into multiple parts. You can learn more about this in the next chapter
- A trigger cannot contain equality or disequality (
==,===,!=, or!==), any basic integer arithmetic operator (like<=or+), or any basic boolean operator (like&&)
Suppose we want to choose the following invalid trigger, 0 <= i:
proof fn test_use_forall_bad1(s: Seq<int>)
requires
5 <= s.len(),
forall|i: int| (#[trigger](0 <= i)) && i < s.len() ==> is_even(s[i]),
{
assert(s[3] % 2 == 0);
}this will result in the following error:
error: trigger must be a function call, a field access, or a bitwise operator
|
| forall|i: int| (#[trigger](0 <= i)) && i < s.len() ==> is_even(s[i]),
| ^^^^^^^^^^^^^^^^^^^^
if we really wanted to, we could make it a valid trigger by introducing an extra function:
spec fn nonnegative(i: int) -> bool {
0 <= i
}
proof fn test_use_forall_bad2(s: Seq<int>)
requires
5 <= s.len(),
forall|i: int| #[trigger] nonnegative(i) && i < s.len() ==> is_even(s[i]),
{
assert(is_even(s[3])); // FAILS: doesn't trigger nonnegative(i)
}but this trigger fails to match because the code doesn’t explicitly mention nonnegative(3)
(you’d have to add an explicit assert(nonnegative(3)) to make the code work).
Good triggers and bad triggers
Going back to our original example:
proof fn test_use_forall_succeeds3(s: Seq<int>)
requires
5 <= s.len(),
forall|i: int| 0 <= i < s.len() ==> is_even(s[i]), // Verus chooses s[i] as the trigger and prints a note
{
assert(s[3] % 2 == 0); // succeeds by triggering s[3]
}So … which trigger is better, s[i] or is_even(s[i])?
Unfortunately, there’s no one best answer to this kind of question.
There are tradeoffs between the two different choices.
The trigger s[i] leads to more pattern matches than is_even(s[i]).
More matches means that the SMT solver is more likely to find relevant
instantiations that help a proof succeed.
However, more matches also mean that the SMT solver is more likely to generate
irrelevant instantiations that clog up the SMT solver with useless information,
slowing down the proof.
In this case, s[i] is probably a good trigger to choose.
It matches whenever the function test_use_forall_succeeds4
talks about an element of the sequence s,
yielding a fact that is likely to be useful for reasoning about s.
Examples for bad choices of triggers would be 0 <= i and nonnegative(i) from the section above:
-
If
0 <= iwas valid, it would match any value that is greater than or equal to 0, which would include values that have nothing to do withsand are unlikely to be relevant tos. -
Furthermore,
nonnegative(i)doesn’t mentions, and the whole point offorall|i: int| 0 <= i < s.len() ==> is_even(s[i])is to say something about the elements ofs, not to say something about nonnegative numbers.
Multiple variables, multiple triggers, matching loops
Suppose we have a forall expression with more than one variable, i and j:
spec fn is_distinct(x: int, y: int) -> bool {
x != y
}
proof fn test_distinct1(s: Seq<int>)
requires
5 <= s.len(),
forall|i: int, j: int| 0 <= i < j < s.len() ==> #[trigger] is_distinct(s[i], s[j]),
{
assert(is_distinct(s[2], s[4]));
}The forall expression shown above says that every element of s is distinct.
(Note: we could have written
0 <= i < s.len() && 0 <= j < s.len() && i != j
instead of
0 <= i < j < s.len(),
but the latter is more concise and is just as general:
given any two distinct integers, we can let i be the smaller one
and j be the larger one so that i < j.)
In the example above, the trigger is_distinct(s[i], s[j])
contains both the variables i and j,
and the expression is_distinct(s[2], s[4]) matches the trigger with i = 2, j = 4:
0 <= 2 < 4 < s.len() ==> is_distinct(s[2], s[4])
Instead of using a function call is_distinct(s[i], s[j]),
we could just write s[i] != s[j] directly.
However, in this case, we cannot use the expression s[i] != s[j] as a trigger,
because, as discussed in the previous section,
triggers cannot contain equalities and disequalities like !=.
However, a trigger does not need to be just a single expression.
It can be split across multiple expressions,
as in the following code, which defines the trigger to be the pair of expressions
s[i], s[j]:
proof fn test_distinct2(s: Seq<int>)
requires
5 <= s.len(),
forall|i: int, j: int| 0 <= i < j < s.len() ==> #[trigger] s[i] != #[trigger] s[j],
{
assert(s[4] != s[2]);
}Verus also supports an alternate, equivalent syntax #![trigger ...],
where the #![trigger ...] immediately follows the forall|...|,
in case we prefer to write the pair s[i], s[j] directly:
proof fn test_distinct3(s: Seq<int>)
requires
5 <= s.len(),
forall|i: int, j: int| #![trigger s[i], s[j]] 0 <= i < j < s.len() ==> s[i] != s[j],
{
assert(s[4] != s[2]);
}When the trigger is the pair s[i], s[j],
there are four matches: i = 2, j = 2 and i = 2, j = 4 and i = 4, j = 2 and i = 4, j = 4:
0 <= 2 < 2 < s.len() ==> s[2] != s[2]
0 <= 2 < 4 < s.len() ==> s[2] != s[4]
0 <= 4 < 2 < s.len() ==> s[4] != s[2]
0 <= 4 < 4 < s.len() ==> s[4] != s[4]
The i = 2, j = 4 instantiation proves s[2] != s[4],
which is equivalent to s[4] != s[2].
The other instantiations are dead ends, since 2 < 2, 4 < 2, and 4 < 4 all fail.
A trigger must mention each of the quantifier variables i and j at least once.
Otherwise, Verus will complain:
proof fn test_distinct_fail1(s: Seq<int>)
requires
5 <= s.len(),
forall|i: int, j: int|
0 <= i < j < s.len() ==> s[i] != #[trigger] s[j], // error: trigger fails to mention i
{
assert(s[4] != s[2]);
}error: trigger does not cover variable i
|
| / ... forall|i: int, j: int|
| | ... 0 <= i < j < s.len() ==> s[i] != #[trigger] s[j], // error: trigger fails to ment...
| |__________________________________________________________^
In order to match a trigger with multiple expressions,
the SMT solver has to find matches for all the expressions in the trigger.
Therefore,
you can always make a trigger more restrictive by adding more expressions to the trigger.
For example, we could gratuitously add a third expression is_even(i)
to the trigger, which would cause the match to fail,
since no expression matches is_even(i):
proof fn test_distinct_fail2(s: Seq<int>)
requires
5 <= s.len(),
forall|i: int, j: int| #![trigger s[i], s[j], is_even(i)]
0 <= i < j < s.len() ==> s[i] != s[j],
{
assert(s[4] != s[2]); // FAILS, because nothing matches is_even(i)
}To make this example succeed, we’d have to mention is_even(2) explicitly:
assert(is_even(2));
assert(s[4] != s[2]); // succeeds; we've matched s[2], s[4], is_even(2)Multiple triggers
In all the examples so far, each quantifier contained exactly one trigger (although the trigger sometimes contained more than one expression). It’s also possible, although rarer, to specify multiple triggers for a quantifier. The SMT solver will instantiate the quantifier if any of the triggers match. Thus, adding more triggers leads to more quantifier instantiations. (This stands in contrast to adding expressions to a trigger: adding more expressions to a trigger makes a trigger more restrictive and leads to fewer quantifier instantiations.)
The following example specifies both #![trigger a[i], b[j]] and #![trigger a[i], c[j]]
as triggers, since neither is obviously better than the other:
proof fn test_multitriggers(a: Seq<int>, b: Seq<int>, c: Seq<int>)
requires
5 <= a.len(),
a.len() == b.len(),
a.len() == c.len(),
forall|i: int, j: int|
#![trigger a[i], b[j]]
#![trigger a[i], c[j]]
0 <= i < j < a.len() ==> a[i] != b[j] && a[i] != c[j],
{
assert(a[2] != c[4]); // succeeds, matches a[i], c[j]
}(Note: to specify multiple triggers, you must use the #![trigger ...] syntax
rather than the #[trigger] syntax.)
If the quantifier had only mentioned the single trigger #![trigger a[i], b[j]],
then the assertion above would have failed, because a[2] != c[4] doesn’t mention b.
A single trigger #![trigger a[i], b[j], c[j]] would be even more restrictive,
requiring both b and c to appear, so the assertion would still fail.
In the example above, you can omit the explicit triggers and
Verus will automatically infer exactly the two triggers
#![trigger a[i], b[j]] and #![trigger a[i], c[j]].
However, in most cases, Verus deliberately avoids inferring more than one trigger,
because multiple triggers lead to more quantifier instantiations,
which potentially slows down the SMT solver.
One trigger is usually enough.
As an example of where one trigger is safer than multiple triggers,
consider an assertion that says that updating element j
of sequence s leaves element i unaffected:
proof fn seq_update_different<A>(s: Seq<A>, i: int, j: int, a: A) {
assert(forall|i: int, j: int|
0 <= i < s.len() && 0 <= j < s.len() && i != j ==> s.update(j, a)[i] == s[i]);
}There are actually two possible triggers for this:
#![trigger s.update(j, a)[i]]
#![trigger s.update(j, a), s[i]]
However, Verus selects only the first one and rejects the second, in order to avoid too many quantifier instantiations:
note: automatically chose triggers for this expression:
|
| assert(forall|i: int, j: int|
| ____________^
| | 0 <= i < s.len() && 0 <= j < s.len() && i != j ==> s.update(j, a)[i] === s[i]
| |_____________________________________________________________________________________^
note: trigger 1 of 1:
--> .\rust_verify\example\guide\quants.rs:243:60
|
| 0 <= i < s.len() && 0 <= j < s.len() && i != j ==> s.update(j, a)[i] === s[i]
| ^^^^^^^^^^^^^^^^^
(Note: you can use the --triggers command-line option to print the message above.)
Matching loops: what they are and to avoid them
Suppose we want to specify that a sequence is sorted.
We can write this in a similar way to the earlier forall expression
about sequence distinctness,
writing s[i] <= s[j] in place of s[i] != s[j]:
proof fn test_sorted_good(s: Seq<int>)
requires
5 <= s.len(),
forall|i: int, j: int| 0 <= i <= j < s.len() ==> s[i] <= s[j],
{
assert(s[2] <= s[4]);
}In Verus, this is the best way to express sortedness,
because the trigger s[i], s[j] works very well.
However, there is an alternate approach.
Instead of quantifying over both i and j,
we could try to quantify over just a single variable i,
and then compare s[i] to s[i + 1]:
proof fn test_sorted_bad(s: Seq<int>)
requires
5 <= s.len(),
forall|i: int|
0 <= i < s.len() - 1 ==> s[i] <= s[i + 1],
{
assert(s[2] <= s[4]);
}However, Verus complains that it couldn’t find any good triggers:
error: Could not automatically infer triggers for this quantifer. Use #[trigger] annotations to manually mark trigger terms instead.
|
| / forall|i: int|
| | 0 <= i < s.len() - 1 ==> s[i] <= s[i + 1],
| |_____________________________________________________^
Verus considers the expressions 0 <= i, i < s.len() - 1, s[i], and s[i + 1]
as candidates for a trigger.
However, all of these except s[i] contain integer arithmetic, which is not allowed in triggers.
The remaining candidate, s[i], looks reasonable at first glance.
Verus nevertheless rejects it, though, because it potentially leads to an infinite matching loop.
Triggers are the way to program the SMT solver’s quantifier instantiations,
and if we’re not careful, we can program infinite loops.
Let’s look at how this can happen.
Suppose that we insist on using s[i] as a trigger:
forall|i: int|
0 <= i < s.len() - 1 ==> #[trigger] s[i] <= s[i + 1],
(TODO: Verus should print a warning about a potential matching loop here.)
This would, in fact, succeed in verifying the assertion s[2] <= s[4],
but not necessarily in a good way.
The SMT solver would match on i = 2 and i = 4.
For i = 2, we’d get:
0 <= 2 < s.len() - 1 ==> s[2] <= s[3]
This creates a new expression s[3], which the SMT can then match on with i = 3:
0 <= 3 < s.len() - 1 ==> s[3] <= s[4]
This tells us s[2] <= s[3] and s[3] <= s[4],
which is sufficient to prove s[2] <= s[4].
The problem is that the instantiations don’t necessarily stop here.
Given s[4], we can match with i = 4, which creates s[5],
which leads to matching with i = 5, and so on:
0 <= 4 < s.len() - 1 ==> s[4] <= s[5]
0 <= 5 < s.len() - 1 ==> s[5] <= s[6]
0 <= 6 < s.len() - 1 ==> s[6] <= s[7]
...
In principle, the SMT solver could loop forever with i = 6, i = 7, and so on.
In practice, the SMT solver imposes a cutoff on quantifier instantiations which often
(but not always) halts the infinite loops.
But even if the SMT solver halts the loop,
this is still an inefficient process,
and matching loops should be avoided.
(For an example of a matching loop that causes the SMT solver to use an infinite
amount of time and memory, see this section.)
exists and choose
exists expressions are the dual of forall expressions.
While forall|i: int| f(i) means that f(i) is true for all i,
exists|i: int| f(i) means that f(i) is true for at least one i.
To prove exists|i: int| f(i),
an SMT solver has to find one value for i such that f(i) is true.
This value is called a witness for exists|i: int| f(i).
As with forall expressions, proofs about exists expressions are based on triggers.
Specifically, to prove an exists expression,
the SMT solver uses the exists expression’s trigger to try to find a witness.
In the following example, the trigger is is_even(i):
proof fn test_exists_succeeds() {
assert(is_even(4));
assert(!is_even(5));
assert(is_even(6));
assert(exists|i: int| #[trigger] is_even(i)); // succeeds with witness i = 4 or i = 6
}There are three expressions that match the trigger:
is_even(4), is_even(5), and is_even(6).
Two of them, is_even(4) and is_even(6) are possible witnesses
for exists|i: int| #[trigger] is_even(i).
Based on these, the assertion succeeds, using either i = 4 or i = 6 as a witness.
By contrast, the same assertion fails in the following code,
since no expressions matching is_even(i) are around:
proof fn test_exists_fails() {
assert(exists|i: int| #[trigger] is_even(i)); // FAILS, no match for trigger
}choose
The proofs above try to prove that an exists expression is true.
Suppose, though, that we already know that an exists expression is true,
perhaps because we assume it as a function precondition.
This means that some witness to the exists expression must exist.
If we want to get the witness, we can use a choose expression.
A choose expression choose|i: int| f(i) implements
the Hilbert choice operator
(sometimes known as epsilon):
it chooses some value i that satisfies f(i) if such a value exists.
Otherwise, it picks an arbitrary value for i.
The following example assumes exists|i: int| f(i) as a precondition.
Based on this, the SMT solver knows that there is at least one witness i
that makes f(i) true,
and choose picks one of these witnesses arbitrarily:
spec fn f(i: int) -> bool;
proof fn test_choose_succeeds()
requires
exists|i: int| f(i),
{
let i_witness = choose|i: int| f(i);
assert(f(i_witness));
}If, on the other hand, we don’t know exists|i: int| f(i),
then choose just returns an arbitrary value that might not satisfy f(i)
(as discussed in ghost vs exec code,
ghost code can create an arbitrary value of any type):
proof fn test_choose_fails() {
let i_witness = choose|i: int| f(i);
assert(i_witness < 0 || i_witness >= 0); // i_witness is some integer
assert(f(i_witness)); // FAILS because we don't know exists|i: int| f(i)
}Regardless of whether we know exists|i: int| f(i) or not,
the choose|i: int| f(i) expression always returns the same value:
proof fn test_choose_same() {
let x = choose|i: int| f(i);
let y = choose|i: int| f(i);
assert(x == y);
}You can also choose multiple values together, collecting the values in a tuple:
spec fn less_than(x: int, y: int) -> bool {
x < y
}
proof fn test_choose_succeeds2() {
assert(less_than(3, 7)); // promote i = 3, i = 7 as a witness
let (x, y) = choose|i: int, j: int| less_than(i, j);
assert(x < y);
}In this example, the SMT solver can prove
exists|i: int, j: int| less_than(i, j)
because the expression less_than(3, 7) matches the
automatically chosen trigger less_than(i, j) when i = 3 and j = 7,
so that i = 3, j = 7 serves as a witness.
Proofs about forall and exists
The previous sections emphasized the importance of triggers
for forall and exists expressions.
Specifically, if you know forall|i| f(i),
then the SMT solver will instantiate i by looking at triggers,
and if you want to prove exists|i| f(i),
then the SMT solver will look at triggers to find a witness i such that f(i) is true.
In other words, using a forall expression relies on triggers
and proving an exists expression relies on triggers.
We can write these cases in the following table:
| proving | using | |
|---|---|---|
| forall | usually just works; otherwise assert-by | triggers |
| exists | triggers | usually just works; otherwise choose |
What about the other two cases,
proving a forall expression and using an exists expression?
These cases are actually easier to automate and do not rely on triggers.
In fact, they often just work automatically,
as in the following examples:
spec fn is_distinct(x: int, y: int) -> bool {
x != y
}
spec fn dummy(i: int) -> bool;
proof fn prove_forall()
ensures
forall|i: int, j: int|
#![trigger dummy(i), dummy(j)]
is_distinct(i, j) ==> is_distinct(j, i),
{
// proving the forall just works; the trigger is irrelevant
}
proof fn use_exists(x: int)
requires
exists|i: int| #![trigger dummy(i)] x == i + 1 && is_distinct(i, 5),
{
// using the exists just works; the trigger is irrelevant
assert(x != 6);
}In these examples, the triggers play no role.
To emphasize this, we’ve used a dummy function for the trigger
that doesn’t even appear anywhere else in the examples,
and the SMT solver still verifies the functions with no difficulty.
(Note, though, that if you called one of the functions above,
then the caller would have to prove the exists expression
or use the forall expression,
and the caller would have to deal with triggers.)
If you want some intuition for why the SMT solver doesn’t rely on triggers to verify the code above, you can think of the verification as being similar to the verification of the following code, where the quantifiers are eliminated and the quantified variables are hoisted into the function parameters:
proof fn hoisted_forall(i: int, j: int)
ensures
is_distinct(i, j) ==> is_distinct(j, i),
{
}
proof fn hoisted_exists(x: int, i: int)
requires
x == i + 1 && is_distinct(i, 5),
{
assert(x != 6);
}Proving forall with assert-by
Sometimes a proof doesn’t “just work” like it does in the simple examples above.
For example, the proof might rely on a lemma that is proved by induction,
which the SMT solver cannot prove completely automatically.
Suppose we have a lemma that proves f(i) for any even i:
spec fn f(i: int) -> bool { ... }
proof fn lemma_even_f(i: int)
requires
is_even(i),
ensures
f(i),
{ ... }Now suppose we want to prove that f(i) is true for all even i:
proof fn test_even_f()
ensures
forall|i: int| is_even(i) ==> f(i), // FAILS because we don't call the lemma
{
}The proof above fails because it doesn’t call lemma_even_f.
If we try to call lemma_even_f, though, we immediately run into a problem:
we need to pass i as an argument to the lemma,
but i isn’t in scope:
proof fn test_even_f()
ensures
forall|i: int| is_even(i) ==> f(i),
{
lemma_even_f(i); // ERROR: i is not in scope here
}To deal with this, Verus supports a special form of assert ... by
for proving forall expressions:
proof fn test_even_f()
ensures
forall|i: int| is_even(i) ==> f(i),
{
assert forall|i: int| is_even(i) implies f(i) by {
// First, i is in scope here
// Second, we assume is_even(i) here
lemma_even_f(i);
// Finally, we have to prove f(i) here
}
}Inside the body of the assert ... by,
the variables of the forall are in scope
and the left-hand side of the ==> is assumed.
This allows the body to call lemma_even_f(i).
Using exists with choose
The example above needed to bring a forall quantifier variable into scope
in order to call a lemma.
A similar situation can arise for exists quantifier variables.
Suppose we have the following lemma to prove f(i):
spec fn g(i: int, j: int) -> bool { ... }
proof fn lemma_g_proves_f(i: int, j: int)
requires
g(i, j),
ensures
f(i),
{ ... }If we know that there exists some j such that g(i, j) is true,
we should be able to call lemma_g_proves_f.
However, we run into the problem that j isn’t in scope:
proof fn test_g_proves_f(i: int)
requires
exists|j: int| g(i, j),
ensures
f(i),
{
lemma_g_proves_f(i, j); // ERROR: j is not in scope here
}In this situation,
we can use choose (discussed in the previous section)
to extract the value j from the exists expression:
proof fn test_g_proves_f(i: int)
requires
exists|j: int| g(i, j),
ensures
f(i),
{
lemma_g_proves_f(i, choose|j: int| g(i, j));
}Example: binary search
Let’s see how forall and exists work in a larger example.
The following code searches for a value k in a sorted sequence
and returns the index r where k resides.
fn binary_search(v: &Vec<u64>, k: u64) -> (r: usize)
requires
forall|i: int, j: int| 0 <= i <= j < v.len() ==> v[i] <= v[j],
exists|i: int| 0 <= i < v.len() && k == v[i],
ensures
r < v.len(),
k == v[r as int],
{
let mut i1: usize = 0;
let mut i2: usize = v.len() - 1;
while i1 != i2
invariant
i2 < v.len(),
exists|i: int| i1 <= i <= i2 && k == v[i],
forall|i: int, j: int| 0 <= i <= j < v.len() ==> v[i] <= v[j],
decreases i2 - i1,
{
let ix = i1 + (i2 - i1) / 2;
if v[ix] < k {
i1 = ix + 1;
} else {
i2 = ix;
}
}
i1
}
fn main() {
let mut v: Vec<u64> = Vec::new();
v.push(0);
v.push(10);
v.push(20);
v.push(30);
v.push(40);
assert(v[3] == 30); // needed to trigger exists|i: int| ... k == v[i]
let r = binary_search(&v, 30);
assert(r == 3);
}The precondition exists|i: int| 0 <= i < v.len() && k == v[i]
specifies that k is somewhere in the sequence,
so that the search is guaranteed to find it.
The automatically inferred trigger for this exists expression is v[i].
The main function satisfies this with the witness i = 3 so that 30 == v[3]:
assert(v[3] == 30); // needed to trigger exists|i: int| ... k == v[i]
let r = binary_search(&v, 30);
The search proceeds by keeping two indices i1 and i2 that
narrow in on k from both sides,
so that the index containing k remains between i1 and i2
throughout the search:
exists|i: int| i1 <= i <= i2 && k == v[i]
In order for the loop to exit, the loop condition i1 != i2 must be false,
which means that i1 and i2 must be equal.
In this case, the i in the exists expression above must be equal to i1 and i2,
so we know k == v[i1],
so that we can return the result i1.
Proving that the loop invariant is maintained
In each loop iteration, we can assume that the loop invariants hold before the iteration,
and we have to prove that the loop invariants hold after the iteration.
Let’s look in more detail at the proof of the invariant
exists|i: int| i1 <= i <= i2 && k == v[i],
focusing on how the SMT solver handles the forall and exists quantifiers.
The key steps are:
- Knowing
exists|i: int| ... k == v[i]gives us a witnessi_witnesssuch thatk == v[i_witness]. - The witness
i_witnessfrom the current iteration’sexists|i: int| ...serves as the witness for the next iteration’sexists|i: int| .... - The comparison
*v.index(ix) < ktells us whetherv[ix] < korv[ix] >= k. - The expressions
v[i_witness]andv[ix]match the triggerv[i], v[j]trigger in the expressionforall|i: int, j: int| ... v[i] <= v[j].
We’ll now walk through these steps in more detail. (Feel free to skip ahead if this is too boring — as the next subsection discusses, the whole point is that the SMT solver takes care of the boring details automatically if we set things up right.)
There are two cases to consider, one where the if condition *v.index(ix) < k is true and one
where *v.index(ix) < k is false.
We’ll just look at the former, where v[ik] < k.
We assume the loop invariant at the beginning of the loop iteration:
exists|i: int| i1 <= i <= i2 && k == v[i]
This tells us that there is some witness i_witness such that:
i1 <= i_witness <= i2 && k == v[i_witness]
In the case where *v.index(ix) < k is true, we execute i1 = ix + 1:
let ix = i1 + (i2 - i1) / 2;
if *v.index(ix) < k {
i1 = ix + 1;
} else {Since the new value of i1 is ix + 1,
we’ll need to prove the loop invariant with ix + 1 substituted for i1:
exists|i: int| ix + 1 <= i <= i2 && k == v[i]
To prove an exists expression, the SMT solver needs to match the expression’s trigger.
The automatically chosen trigger for this expression is v[i],
so the SMT solver looks for expressions of the form v[...].
It finds v[i_witness] from the previous loop invariant (shown above).
It also finds v[ix] from the call v.index(ix) in the expression *v.index(ix) < k.
Based on these, it attempts to prove ix + 1 <= i <= i2 && k == v[i]
with i = i_witness or i = ix:
ix + 1 <= i_witness <= i2 && k == v[i_witness]
ix + 1 <= ix <= i2 && k == v[ix]
The i = ix case is a dead end, because ix + 1 <= ix is never true.
The i = i_witness case is more promising.
We already know i_witness <= i2 and k == v[i_witness]
from our assumptions about i_witness at the beginning of the loop iteration.
We just need to prove ix + 1 <= i_witness.
We can simplify this to ix < i_witness.
Proving ix < i_witness
To prove ix < i_witness, we now turn to the forall loop invariant:
forall|i: int, j: int| 0 <= i <= j < v.len() ==> v[i] <= v[j],
In order to instantiate this, the SMT solver again relies on triggers.
In this forall, expression, the trigger is v[i], v[j],
so again the SMT solver looks for terms of the form v[...]
and finds v[i_witness] and v[ix].
There are four different possible assignments of i_witness and ix to i and j.
0 <= i_witness <= i_witness < v.len() ==> v[i_witness] <= v[i_witness]
0 <= i_witness <= ix < v.len() ==> v[i_witness] <= v[ix]
0 <= ix <= i_witness < v.len() ==> v[ix] <= v[i_witness]
0 <= ix <= ix < v.len() ==> v[ix] <= v[ix]
Out of these, the second one is most useful:
0 <= i_witness <= ix < v.len() ==> v[i_witness] <= v[ix]
We already know k == v[i_witness], so this becomes:
0 <= i_witness <= ix < v.len() ==> k <= v[ix]
The right-hand side of the ==> says k <= v[ix],
which contradicts our assumption that v[ik] < k in the case where *v.index(ix) < k.
This means that the left-hand side of the ==> must be false:
!(0 <= i_witness <= ix < v.len())
The SMT solver knows that 0 <= i_witness and ix < v.len(),
so it narrows this down to:
!(i_witness <= ix)
This tells us that ix < i_witness, which is what we want.
Helping the automation succeed
As seen in the previous section, proving the loop invariant requires a long chain of reasoning. Fortunately, the SMT solver performs all of these steps automatically. In fact, this is a particularly fortunate example, because Verus automatically chooses the triggers as well, and these triggers happen to be just what the SMT solver needs to complete the proof.
In general, though, how we express the preconditions, postconditions, and loop invariants has a big influence on whether Verus and the SMT solver succeed automatically. Suppose, for example, that we had written the sortedness condition (in the precondition and loop invariant) as:
forall|i: int| 0 <= i < v.len() - 1 ==> #[trigger] v[i] <= v[i + 1]
instead of:
forall|i: int, j: int| 0 <= i <= j < v.len() ==> v[i] <= v[j]
As discussed in a previous section,
the trigger v[i] in combination with v[i] <= v[i + 1] leads to a matching loop,
which can send the SMT solver into an infinite loop.
This is, in fact, exactly what happens:
error: while loop: Resource limit (rlimit) exceeded; consider rerunning with --profile for more details
|
| / while i1 != i2
| | invariant
| | i2 < v.len(),
| | exists|i: int| i1 <= i <= i2 && k == v[i],
|
| | }
| | }
| |_____^
Even if the SMT solver had avoided the infinite loop, though,
it’s hard to see how it could have succeeded automatically.
As discussed above, a crucial step involves instantiating
i = i_witness and j = ix to learn something about v[i_witness] <= v[ix].
This simply isn’t a possible instantiation when there’s only one variable i
in the forall expression.
Learning something about v[i_witness] <= v[ix] would require chaining together
an arbitrarily long sequence of v[i] <= v[i + 1] steps to get from
i_witness to i_witness + 1 to i_witness + 2 all the way to ix.
This would require a separate proof by induction.
Intuitively, the expression v[i] <= v[j]
is better suited than v[i] <= v[i + 1]
to an algorithm like binary search that takes large steps from one index to another,
because i and j can be arbitrarily far apart,
whereas i and i + 1 are only one element apart.
When the SMT automation fails, it’s often tempting to immediately start adding asserts,
lemmas, proofs by induction, etc., until the proof succeeds.
Given enough manual effort, we could probably finish a proof of binary search with the problematic
v[i] <= v[i + 1] definition of sortedness.
But this would be a mistake;
it’s better to structure the definitions in a way that helps the automation succeed
without so much manual effort.
If you find yourself writing a long manual proof,
it’s worth stepping back and figuring out why the automation is failing;
maybe a change of definitions can fix the failure in the automation.
After all, if your car breaks down, it’s usually better to fix the car than to push it.
Adding Ambient Facts to the Proof Environment with broadcast
In a typical Verus project, a developer might prove a fact (e.g., pushing an element into a sequence does not change the elements already in the sequence) in a proof function, e.g.,
pub proof fn seq_contains_orig_elems_after_push<A>(s:Seq<A>, v:A, x:A)
requires s.contains(x)
ensures s.push(v).contains(x)
{
...
}To make use of this fact, the developer must explicitly invoke the proof function, e.g.,
proof fn example<A>(s: Seq<A>, v: A, x: A) {
assume(s.contains(x));
let t = s.push(v);
// assert(t.contains(x)); // FAILS
seq_contains_orig_elems_after_push(s, v, x); // Adds the proof's fact to the proof environment
assert(t.contains(x)); // SUCCEEDS
}However, in some cases, a proof fact is so useful that a developer always wants it to be in scope, without manually invoking the corresponding proof. For example, the fact that an empty sequence’s length is zero is so “obvious” that most programmers will expect Verus to always know it. This feature should be used with caution, however, as every extra ambient fact slows the prover’s overall performance.
Suppose that after considering the impact on the solver’s performance, the
programmer decides to make the above fact about push ambient. To do so,
they can add the broadcast modifier in the
definition of seq_contains_orig_elems_after_push: pub broadcast proof fn seq_contains_orig_elems_after_push<A>(s: Seq<A>, v:A, x:A).
The effect is to introduce the following
quantified fact to the proof environment:
forall |s: Seq<A>, v: A, x: A| s.contains(x) ==> s.push(v).contains(x)Because this introduces a quantifier, Verus will typically ask you to
explicitly choose a trigger, e.g., by adding a #[trigger] annotation.
Hence, the final version of our example might look like this:
pub broadcast proof fn seq_contains_orig_elems_after_push<A>(s:Seq<A>, v:A, x:A)
requires s.contains(x)
ensures #[trigger] s.push(v).contains(x)
{
...
}To bring this ambient lemma into scope, for a specific proof, or for an entire
module, you can use broadcast use seq_contains_orig_elems_after_push;.
Some of these broadcast-ed lemmas are available in the verus standard library vstd,
some as part of broadcast “groups”, which combine a number of properties into a single
group name, which can be brought into scope with broadcast use broadcast_group_name;.
For example, the example above can all be automatically proved from broadcast use vstd::seq_lib::group_seq_properties;.
We are working on extending the discoverability of these groups in the standard library
documentation: they currently appear as regular functions.
Experimental broadcast lemma usage information
You can use the -V axiom-usage-info experimental flag to obtain an overapproximation
of the broadcasted axioms and lemmas that were used in the verification of each function.
For large projects, use --verify-only-module and possibly --verify-function to limit the
amount of output.
As an example, using -V axiom-usage-info on examples/broadcast_proof.rs produces this information for the increase_twice function:
note: checking this function used these broadcasted lemmas and broadcast groups:
- (group) broadcast_proof::multiple_broadcast_proof::Multiple::group_properties,
- broadcast_proof::multiple_broadcast_proof::Multiple::lemma_add_aligned
--> ../examples/broadcast_proof.rs:161:11
|
161 | proof fn increase_twice(
| ___________^
162 | | p1: Multiple, v: Multiple, p2: Multiple)
| |________________________________________________^
indicating that the group_properties group enabled the use of lemma_add_aligned, which was
likely used in the proof.
SMT solving and automation
Sometimes an assertion will fail even though it’s true. At a high level, Verus
works by generating formulas called “verification conditions” from a program’s
assertions and specifications (requires and ensures clauses); if these
verification conditions are always true, then all of the assertions and
specifications hold. The verification conditions are checked by an SMT solver
(Z3), and therefore Verus is limited by Z3’s ability to prove generated
verification conditions.
This section walks through the reasons why a proof might fail.
The first reason why a proof might fail is that the statement is wrong! If there is a bug in a specification or assertion, then we hope that Z3 will not manage to prove it. We won’t talk too much about this case in this document, but it’s important to keep this in mind when debugging proofs.
The core reason for verification failures is that proving the verification conditions from Verus is an undecidable task: there is no algorithm that can prove general formulas true. In practice Z3 is good at proving even complex formulas are true, but there are some features that lead to inconclusive verification results.
Quantifiers: Proving theorems with quantifiers (exists and forall) is
in general undecidable. For Verus, we rely on Z3’s pattern-based instantiation
of quantifiers (“triggers”) to use and prove formulas with quantifiers. See the
section on forall and triggers for more details.
Opaque and closed functions: Verification conditions by default hide the bodies of opaque and closed functions; revealing those bodies might make verification succeed, but Verus intentionally leaves this to the user to improve performance and allow hiding where desired.
Inductive invariants: Reasoning about recursion (loops, recursive lemmas) requires an inductive invariant, which Z3 cannot in general come up with.
Extensional equality assertions: If a theorem requires extensional equality
(eg, between sequences, maps, or spec functions), this typically requires
additional assertions in the proof. The key challenge is that there are many
possible sequence expressions (for example) in a program that Z3 could attempt
to prove are equal. For performance reasons Z3 cannot attempt to prove all
pairs of expressions equal, both because there are too many (including the
infinitely many not in the program at all) and because each proof involves
quantifiers and is reasonably expensive. The result is that a proof may start
working if you add an equality assertion: the assertion explicitly asks Z3 to
prove and use an equality.
See extensional equality for how to use the
extensional equality operators =~= and =~~=.
Incomplete axioms: The standard library includes datatypes like Map and
Seq that are implemented using axioms that describe their expected
properties. These axioms might be incomplete; there may be a property that you
intuitively expect a map or sequence to satisfy but which isn’t implied by the
axioms, or which is implied but requires a proof by induction.
If you think this is the case, please open an issue or a pull request adding
the missing axiom.
Slow proofs: Z3 may be able to find a proof but it would simply take too long. We limit how long Z3 runs (using its resource limit or “rlimit” feature so that this limit is independent of how fast the computer is), and consider it a failure if Z3 runs into this limit. The philosophy of Verus is that it’s better to improve solver performance than rely on a slow proof. Improving SMT performance talks more about what you can do to diagnose and fix poor verification performance.
Integers: Nonlinear Arithmetic
Generally speaking, Verus’s default solver (Z3) is excellent at handling linear integer arithmetic.
Linear arithmetic captures equalities, inequalities, addition, subtraction, and multiplication and division by constants.
This means it’s great at handling expressions like 4 * x + 3 * y - z <= 20. However, it is less capable
when nonlinear expressions are involved, like x * y (when neither x nor y can be substituted for a constant)
or x / y (when y cannot be substituted for a constant).
That means many common axioms are inaccessible in the default mode, including but not limited to:
x * y == y * xx * (y * z) == (x * y) * zx * (a + b) == x * a + x * b0 <= x <= y && 0 <= z <= w ==> x * z <= y * w
The reason for this limitation is that Verus intentionally disables theories of nonlinear arithmetic in its default prover mode.
However, it is possible to opt-in to nonlinear reasoning by invoking a specialized prover mode. There are two prover modes related to nonlinear arithmetic.
nonlinear_arith- Enable Z3’s nonlinear theory of arithmetic.integer_ring- Enable a decidable, equational theory of rings.
The first is general-purpose, but unfortunately it is somewhat unpredicable. (This is why it is turned off by default.) The second handles a more specific class of problems, but it is decidable and efficient. Invoking either prover mode requires an understanding of how to minimize prover context. We describe each of these modes in more detail below.
Note that if neither mode works for your proof, you can also manually invoke a lemma from Verus’s arithmetic library, which supplies a large collection of verified facts about how nonlinear operations behave. For example, the inaccessible properties listed above can be proven by invoking
lemma_mul_is_commutativelemma_mul_is_associativelemma_mul_is_distributive_addlemma_mul_upper_bound
respectively. If your proof involves using multiple such lemmas, you may want to use a structured proof to make the proof more readable and easier to maintain.
1. Invoking a specialized solver: nonlinear_arith
A specialized solver is invoked with the by keyword, which can be applied to either
an assert statement or a proof fn.
Here, we’ll see how it works using the nonlinear_arith solver,
which enables Z3’s theory of nonlinear arithmetic for integers.
Inline Proofs with assert(...) by(nonlinear_arith)
To prove a nonlinear property in the midst of a larger function,
you can write assert(...) by(nonlinear_arith). This creates
a separate Z3 query just to prove the asserted property,
and for this query, Z3 runs with its nonlinear heuristics enabled.
The query does NOT include ambient facts (e.g., knowledge that stems
from the surrounding function’s requires clause or from preceding variable assignments)
other than that which is:
- inferred from a variable’s type (e.g., the allowed ranges of a
u64ornat), or - supplied explicitly.
To supply context explicitly, you can use a requires clause, a shown below:
proof fn bound_check(x: u32, y: u32, z: u32)
requires
x <= 8,
y <= 8,
{
assert(x * y <= 100) by (nonlinear_arith)
requires
x <= 10,
y <= 10;
assert(x * y <= 1000);
}Let’s go through this example, one step at a time:
- Verus uses its normal solver to prove the assert’s
requiresclause, thatx <= 10 && y <= 10. This follows from the precondition of the function. - Verus uses Z3’s nonlinear solver to prove
x <= 10 && y <= 10 ==> x * y <= 100. This would not be possible with the normal solver, but it is possible for the nonlinear solver. - The fact
x * y <= 100is now provided in the proof context for later asserts. - Verus uses its normal solver to prove that
x * y <= 1000, which follows fromx * y <= 100.
Furthermore, if you use a by clause, as in assert ... by(nonlinear_arith) by { ... }, then everything in the by clause will opt-in to the nonlinear solver.
Reusable proofs with proof fn ... by(nonlinear_arith)
You can also use by(nonlinear_arith) in a proof function’s signature. By including by(nonlinear_arith), the query for this function runs with nonlinear arithmetic reasoning enabled. For example:
proof fn bound_check2(x: u32, y: u32, z: u32) by (nonlinear_arith)
requires
x <= 8,
y <= 8,
ensures
x * y <= 64
{ }When a specialized solver is invoked on a proof fn like this, it is used to prove the
lemma. When the lemma is then invoked from elsewhere, Verus (as usual) proves that the
precondition is met; for this it uses its normal solver.
2. Proving Ring-based Properties: integer_ring
While general nonlinear formulas cannot be solved consistently, certain
sub-classes of nonlinear formulas can be. For example, nonlinear formulas that
consist of a series of congruence relations (i.e., equalities modulo some
divisor n). As a simple example, we might like to show that a % n == b % n ==> (a * c) % n == (b * c) % n.
Verus offers a deterministic proof strategy to discharge such obligations.
The strategy is called integer_ring.
[Note: at present, it is only possible to invoke integer_ring using the
proof fn ... by(integer_ring) style; inline asserts are not supported.]
Verus will then discharge the proof obligation using a dedicated algebra solver called Singular. As hinted at by the annotation, this proof technique is only complete (i.e., guaranteed to succeed) for properties that are true for all rings. Formulas that rely specifically on properties of the integers may not be solved successfully.
Using this proof technique requires a bit of additional configuration of your Verus installation. See installing and setting up Singular.
Details/Limitations
- This can be used only with int parameters.
- Formulas that involve inequalities are not supported.
- Division is not supported.
- Function calls in the formulas are treated as uninterpreted functions. If a function definition is important for the proof, you should unfold the definition of the function in the proof function’s
requiresclause. - When using an
integer_ringlemma, the divisor of a modulus operator (%) must not be zero. If a divisor can be zero in the ensures clause of theinteger_ringlemma, the facts in the ensures clause will not be available in the callsite.
To understand what integer_ring can or cannot do, it is important to understand how it
handles the modulus operator, %. Since integer_ring does not understand inequalities,
it cannot perform reasoning that requires that 0 <= (a % b) < b.
As a result, Singular’s results might be confusing if you think of % primarily
as the operator you’re familiar with from programming.
For example, suppose you use a % b == x as a precondition.
Encoded in Singular, this will become a % b == x % b, or in more traditional “mathematical”
language, a ≡ x (mod b). This does not imply that x is in the range [0, b),
it only implies that a and x are in the same equivalence class mod b.
In other words, a % b == x implies a ≡ x (mod b), but not vice versa.
For the same reason, you cannot ask the integer_ring solver to prove a postcondition
of the form a % b == x, unless x is 0. The integer_ring solver can prove
that a ≡ x (mod b), equivalently (a - x) % b == 0, but this does not imply
that a % b == x.
Let’s look at a specific example to understand the limitation.
proof fn foo(a: int, b: int, c: int, d: int, x: int, y: int) by(integer_ring)
requires
a == c,
b == d,
a % b == x,
c % d == y
ensures
x == y,
{
}This theorem statement appears to be trivial, and indeed, Verus would solve it easily
using its default proof strategy.
However, integer_ring will not solve it.
We can inspect the Singular query to understand why.
(See here for how to log these.)
ring ring_R=integer, (a, b, c, d, x, y, tmp_0, tmp_1, tmp_2), dp;
ideal ideal_I =
a - c,
b - d,
(a - (b * tmp_0)) - x,
(c - (d * tmp_1)) - y;
ideal ideal_G = groebner(ideal_I);
reduce(x - y, ideal_G);
quit;
We can see here that a % b is translated to a - b * tmp_0,
while c % d is translated to c - d * tmp_1.
Again, since there is no constraint that a - b * tmp_0 or c - d * tmp_1
is bounded, it is not possible to conclude
that a - b * tmp_0 == c - d * tmp_1 after this simplification has taken place.
3. Combining integer_ring and nonlinear_arith.
As explained above, the integer_ring feature has several limitations, it is not possible to get an arbitary nonlinear property only with the integer_ring feature. Instead, it is a common pattern to have a by(nonlinear_arith) function as a main lemma for the desired property, and use integer_ring lemma as a helper lemma.
To work around the lack of support for inequalities and division, you can often write a helper proof discharged with integer_ring and use it to prove properties that are not directly supported by integer_ring. Furthermore, you can also add additional variables to the formulas. For example, to work around division, one can introduce c where b = a * c, instead of b/a.
Example 1: integer_ring as a helper lemma to provide facts on modular arithmetic
In the lemma_mod_difference_equal function below, we have four inequalities inside the requires clauses, which cannot be encoded into integer_ring. In the ensures clause, we want to prove y % d - x % d == y - x. The helper lemma lemma_mod_difference_equal_helper simply provides that y % d - x % d is equal to (y - x) modulo d. The rest of the proof is done by by(nonlinear_arith).
pub proof fn lemma_mod_difference_equal_helper(x: int, y:int, d:int, small_x:int, small_y:int, tmp1:int, tmp2:int) by(integer_ring)
requires
small_x == x % d,
small_y == y % d,
tmp1 == (small_y - small_x) % d,
tmp2 == (y - x) % d,
ensures
(tmp1 - tmp2) % d == 0
{}
pub proof fn lemma_mod_difference_equal(x: int, y: int, d: int) by(nonlinear_arith)
requires
d > 0,
x <= y,
x % d <= y % d,
y - x < d
ensures
y % d - x % d == y - x
{
let small_x = x % d;
let small_y = y % d;
let tmp1 = (small_y - small_x) % d;
let tmp2 = (y - x) % d;
lemma_mod_difference_equal_helper(x,y,d, small_x, small_y, tmp1, tmp2);
}In the lemma_mod_between function below, we want to prove that x % d <= z % d < y % d. However, integer_ring only supports equalities, so we cannot prove lemma_mod_between directly. Instead, we provide facts that can help assist the proof. The helper lemma provides 1) x % d - y % d == x - y (mod d) and 2) y % d - z % d == y - z (mod d). The rest of the proof is done via by(nonlinear_arith).
pub proof fn lemma_mod_between_helper(x: int, y: int, d: int, small_x:int, small_y:int, tmp1:int) by(integer_ring)
requires
small_x == x % d,
small_y == y % d,
tmp1 == (small_x - small_y) % d,
ensures
(tmp1 - (x-y)) % d == 0
{}
// note that below two facts are from the helper function, and the rest are done by `by(nonlinear_arith)`.
// x % d - y % d == x - y (mod d)
// y % d - z % d == y - z (mod d)
pub proof fn lemma_mod_between(d: int, x: int, y: int, z: int) by(nonlinear_arith)
requires
d > 0,
x % d < y % d,
y - x <= d,
x <= z < y
ensures
x % d <= z % d < y % d
{
let small_x = x % d;
let small_y = y % d;
let small_z = z % d;
let tmp1 = (small_x - small_z) % d;
lemma_mod_between_helper(x,z,d, small_x, small_z, tmp1);
let tmp2 = (small_z - small_y) % d;
lemma_mod_between_helper(z,y,d, small_z, small_y, tmp2);
}Example 2: Proving properties on bounded integers with the help of integer_ring
Since integer_ring proofs only support int, you need to include explicit bounds when you want to prove properties about bounded integers. For example, as shown below, in order to use the proof lemma_mod_after_mul on u32s, lemma_mod_after_mul_u32 must ensure that all arguments are within the proper bounds before passing them to lemma_mod_after_mul.
If a necessary bound (e.g., m > 0) is not included, Verus will fail to verify the proof.
proof fn lemma_mod_after_mul(x: int, y: int, z: int, m: int) by (integer_ring)
requires (x-y) % m == 0
ensures (x*z - y*z) % m == 0
{}
proof fn lemma_mod_after_mul_u32(x: u32, y: u32 , z: u32, m: u32)
requires
m > 0,
(x-y) % (m as int) == 0,
x >= y,
x <= 0xffff,
y <= 0xffff,
z <= 0xffff,
m <= 0xffff,
ensures (x*z - y*z) % (m as int) == 0
{
lemma_mod_after_mul(x as int, y as int, z as int, m as int);
// rest of proof body omitted for space
}The desired property for nat can be proved similarly.
The next example is similar, but note that we introduce several additional variables(ab, bc, and abc) to help with the integer_ring proof.
pub proof fn multiple_offsed_mod_gt_0_helper(a: int, b: int, c: int, ac: int, bc: int, abc: int) by (integer_ring)
requires
ac == a % c,
bc == b % c,
abc == (a - b) % c,
ensures (ac - bc - abc) % c == 0
{}
pub proof fn multiple_offsed_mod_gt_0(a: nat, b: nat, c: nat) by (nonlinear_arith)
requires
a > b,
c > 0,
b % c == 0,
a % c > 0,
ensures (a - b) % (c as int) > 0
{
multiple_offsed_mod_gt_0_helper(
a as int,
b as int,
c as int,
(a % c) as int,
(b % c) as int,
((a - b) % (c as int)) as int
);
}More integer_ring examples can be found in this folder, and this testcase file.
Examining the encoding
Singular queries will be logged to the directory specified with --log-dir (which defaults to .verus-log) in a the .air file for the module containing the file.
Bit vectors and bitwise operations
In its default prover mode, Verus treats bitwise operations like &, |, ^, << and >> as uninterpreted functions.
Even basic facts like x & y == y & x are not exported by Verus’s default solver mode.
To handle these situations, Verus provides the specialized solver mode bit_vector.
This solver is great for properties about bitwise operators, and it can also handle
some bounded integer arithmetic, though for this, its efficacy varies.
Invoking the bit_vector prover mode.
The bit_vector prover mode can be invoked
similarly to nonlinear_arith,
with by(bit_vector) either on an assert or a proof fn.
Using by(bit_vector) on an assert lets one assert a short and context-free
bit-manipulation property, as in the following examples:
fn test_passes(b: u32) {
assert(b & 7 == b % 8) by (bit_vector);
assert(b & 0xff < 0x100) by (bit_vector);
}As with nonlinear_arith, assertions expressed via assert(...) by(bit_vector) do not include any ambient facts from the surrounding context (e.g., from the surrounding function’s requires clause or from previous variable assignments). For example, the following example will fail:
fn test_fails(x: u32, y: u32)
requires x == y
{
assert(x & 3 == y & 3) by(bit_vector); // Fails
}But context can be imported explicitly with a requires clause:
fn test_success(x: u32, y: u32)
requires
x == y,
{
assert(x & 3 == y & 3) by (bit_vector)
requires
x == y,
; // now x == y is available for the bit_vector proof
}Attaching by(bit_vector) to a proof function f makes Verus use
the bit_vector solver when verifying f. But note when another function
calls f, Verus uses the normal solver to verify that it satisfies all the
preconditions of f. Here’s an example of using by(bit_vector) on a proof
function:
proof fn de_morgan_auto()
by (bit_vector)
ensures
forall|a: u32, b: u32| #[trigger] (!(a & b)) == !a | !b,
forall|a: u32, b: u32| #[trigger] (!(a | b)) == !a & !b,
{
}How the bit_vector solver works and what it’s good at
The bit_vector solver uses a different SMT encoding, though one where all arithmetic operations
have the same semantic meaning.
Specifically, it encodes all integers into the Z3 bv type and encodes arithmetic via the built-in bit-vector operations.
Internally, the SMT solver uses a technique called “bit blasting”.
To implement this encoding, Verus needs to choose an appropriate bit width to represent
any given integer. For symbolic, fixed-width integer values (e.g., u64) it can just choose
the appropriate bitwidth (e.g., 64 bits). For the results of arithmetic operations,
Verus chooses an appropriate bitwidth automatically.
However, for this reason, the bitvector solver cannot reason over symbolic integer values.
The bit_vector solver is ideal for proofs about bitwise operations
(&, |, ^, <<, and >>).
However, it can also be decent at arithmetic (+, -, *, /, %) over bounded integers.
Examples and tips
Functions
The bit_vector solver supports the use of constants and spec functions.
However, those functions are still restricted to using the same bit-vector and
arithemtic operations listed above (internally, function support works by
inlining the functions).
Function support means that you can write and use descriptive helper functions. For example, you might define:
spec fn get_bit(val: u32, index: u32) -> bool {
0x1u32 & (val >> index) == 1
}
fn test_get_bit() {
assert(get_bit(128u32, 7)) by (bit_vector);
}Note that recursive functions are only supported if they can be statically determined to terminate (e.g., computing Fibonacci on a constant).
If you want to reason about a function opaquely (i.e., without inlining its body), you can assign its result to a (ghost) variable and then use it in a bit-vector assertion. For example:
proof fn test_overflow_check(a: u8, b: u8) {
// Because we call `complex_f` here, it remains opaque in the assertion.
let c = complex_f(a, b);
assert(c >> 1 == c / 2) by(bit_vector);
}Overflow checking
Though the bit_vector solver does not handle symbolic int values, it does support many
arithmetic operations that return int values.
This makes it possible to write conditions about overflow:
proof fn test_overflow_check(a: u8, b: u8) {
// `a` and `b` are both `u8` integers, but we can test if their addition
// overflows a `u8` by simply writing `a + b < 256`.
assert((a & b) == 0 ==> (a | b) == (a + b) && (a + b) < 256) by(bit_vector);
}Integer wrapping and truncation
The bit_vector solver is one of the easiest ways to reason about truncation, which can be naturally expressed through bit operations.
proof fn test_truncation(a: u64) {
assert(a as u32 == a & 0xffff_ffff) by(bit_vector);
// You can write an identity with modulus as well:
assert(a as u32 == a % 0x1_0000_0000) by(bit_vector);
}You may also find it convenient to use add, sub, and mul, which (unlike +, -, and *) automatically truncate.
proof fn test_truncating_add(a: u64, b: u64) {
assert(add(a, b) == (a + b) as u64) by(bit_vector);
}Working with usize and isize
If you use variables of type usize or isize, the bit_vector solver (by default) assumes they
might be either 32-bit or 64-bit, which affects the encoding.
In that case, the solver will generate 2 different queries and verify both.
However, the solver can also be configured to assume a particular platform size.
Bitwidth dependence and independence
For many operations, their results are independent of the input bitwidths.
This is true of &, |, ^, and >>.
In fact, we don’t even need the bit_vector solver to prove this; the normal solver mode is “aware”
of this fact as well.
proof fn test_xor_u32_vs_u64(x: u32, y: u32) {
assert((x as u64) ^ (y as u64) == (x ^ y) as u64) by(bit_vector);
// XOR operation is independent of bitwidth so we don't even
// need the `bit_vector` solver to do this:
assert((x as u64) ^ (y as u64) == (x ^ y) as u64);
}However, this is not true of left shift, <<.
With left shift, you always need to be careful of the bitwidth of the left operand.
proof fn test_left_shift_u32_vs_u64(y: u32) {
assert(1u32 << y == 1u64 << y); // FAILS (in either mode) because it's not true
}More examples
Some larger examples to browse:
Equality via extensionality
The specification libraries section
introduced the extensional equality operator =~=
to check equivalence for collection types like Seq, Set, and Map.
Extensional equality proves that two collections are equal by proving that
the collections contain equal elements.
This can be used, for example, to prove that the sequences s1, s2, and s3
are equal because they have the same elements (0, 10, 20, 30, 40),
even though this sequences were constructed in different ways:
proof fn check_eq(x: Seq<int>, y: Seq<int>)
requires
x == y,
{
}
proof fn test_eq2() {
let s1: Seq<int> = seq![0, 10, 20, 30, 40];
let s2: Seq<int> = seq![0, 10] + seq![20] + seq![30, 40];
let s3: Seq<int> = Seq::new(5, |i: int| 10 * i);
assert(s1 =~= s2);
assert(s1 =~= s3);
check_eq(s1, s2); // succeeds
check_eq(s1, s3); // succeeds
}Assertions like assert(s1 =~= s2) are common for proving equality via extensionality.
Note that by default, Verus promotes == to =~= inside assert, ensures, and invariant,
so that, for example, assert(s1 == s2) actually means assert(s1 =~= s2).
This is convenient in many cases where extensional equality is merely a minor step in a larger proof,
and you don’t want to clutter the proof with low-level details about equality.
For proofs where extensional equality is the key step,
you may want to explicitly write assert(s1 =~= s2) for documentation’s sake.
(If you don’t want Verus to auto-promote == to =~=,
perhaps because you want to see exactly where extensional equality is really needed,
the #[verifier::auto_ext_equal(...)] and #![verifier::auto_ext_equal(...)]
attributes can override Verus’s default behavior.
See ext_equal.rs
for examples.)
Extensional equality for structs and enums
Suppose that a struct or enum datatype has a field containing Seq, Set, and Map,
and suppose that we’d like to prove that two values of the datatype are equal.
We could do this by using =~= on each field individually:
struct Foo {
a: Seq<int>,
b: Set<int>,
}
proof fn ext_equal_struct() {
let f1 = Foo { a: seq![1, 2, 3], b: set!{4, 5, 6} };
let f2 = Foo { a: seq![1, 2].push(3), b: set!{5, 6}.insert(4) };
// assert(f1 == f2); // FAILS -- need to use =~= first
assert(f1.a =~= f2.a); // succeeds
assert(f1.b =~= f2.b); // succeeds
assert(f1 == f2); // succeeds, now that we've used =~= on .a and .b
}However, it’s rather painful to use =~= on each field every time to check for equivalence.
To help with this, Verus supports the #[verifier::ext_equal] attribute
to mark datatypes that need extensionality on Seq, Set, Map, Multiset, spec_fn
fields or fields of other #[verifier::ext_equal] datatypes. For example:
#[verifier::ext_equal] // necessary for invoking =~= on the struct
struct Foo {
a: Seq<int>,
b: Set<int>,
}
proof fn ext_equal_struct() {
let f1 = Foo { a: seq![1, 2, 3], b: set!{4, 5, 6} };
let f2 = Foo { a: seq![1, 2].push(3), b: set!{5, 6}.insert(4) };
assert(f1 =~= f2); // succeeds
}(Note: adding #[verifier::ext_equal] does not change the meaning of ==;
it just makes it more convenient to use =~= to prove == on datatypes.)
Deep extensional equality
Collection datatypes like sequences and sets can contain other collection datatypes as elements
(for example, a sequence of sequences, or set of sequences).
The =~= operator only applies extensionality to the top-level collection,
not to the nested elements of the collection.
To also apply extensionality to the elements,
Verus provides a “deep” extensional equality operator =~~=
that handles arbitrary nesting of collections, spec_fn, and datatypes.
For example:
proof fn ext_equal_nested() {
let inner: Set<int> = set!{1, 2, 3};
let s1: Seq<Set<int>> = seq![inner];
let s2 = s1.update(0, s1[0].insert(1));
let s3 = s1.update(0, s1[0].insert(2).insert(3));
// assert(s2 =~= s3); // FAILS
assert(s2 =~~= s3); // succeeds
let s4: Seq<Seq<Set<int>>> = seq![s1];
let s5: Seq<Seq<Set<int>>> = seq![s2];
assert(s4 =~~= s5); // succeeds
}The same applies to spec_fn, as in:
#[verifier::ext_equal] // necessary for invoking =~= on the struct
struct Bar {
a: spec_fn(int) -> int,
}
proof fn ext_equal_fnspec(n: int) {
// basic case
let f1 = (|i: int| i + 1);
let f2 = (|i: int| 1 + i);
assert(f1 =~= f2); // succeeds
// struct case
let b1 = Bar { a: |i: int| if i == 1 { i } else { 1 } };
let b2 = Bar { a: |i: int| 1int };
assert(b1 =~= b2); // succeeds
// nested case
let i1 = (|i: int| i + 2);
let i2 = (|i: int| 2 + i);
let n1: Seq<spec_fn(int) -> int> = seq![i1];
let n2: Seq<spec_fn(int) -> int> = seq![i2];
// assert(n1 =~= n2); // FAILS
assert(n1 =~~= n2); // succeeds
}Managing proof performance and why it’s critical
Sometimes your proof succeeds, but it takes too long. It’s tempting to simply tolerate the longer verification time and move on. However, we urge you to take the time to improve the verification performance. Slow verification performance typically has an underlying cause. Diagnosing and fixing the cause is much easier to do as the problems arise; waiting until you have multiple performance problems compounds the challenges of diagnosis and repair. Plus, if the proof later breaks, you’ll appreciate having a short code-prove development cycle. Keeping verification times short also makes it easier to check for regressions.
This chapter describes various ways to measure the performance of your proofs and steps you can take to improve it.
Meausuring verification performance
To see a more detailed breakdown of where Verus is spending time, you can pass
--time on the command line. For even more details, try --time-expanded.
For a machine-readable output, add --output-json. These flags will also
report on the SMT resources (rlimit) used. SMT resources are an advanced topic;
they give a very rough estimate of how hard the SMT solver worked on the provided
query (or queries).
See verus --help for more information about these options.
Quantifier Profiling
Sometimes the verification of a Verus function will time out, meaning that the solver couldn’t determine whether all of the proof obligations have been satisfied. Or verification might succeed but take longer than we would like. One common cause for both of these phenomena is quantifiers. If quantifiers (and their associated triggers) are written too liberally (i.e., they trigger too often), then the SMT solver may generate too many facts to sort through efficiently. To determine if this is the case for your Verus code, you can use the built-in quantifier profiler.
As a concrete example, suppose we have the following three functions defined:
uninterp spec fn f(x: nat, y: nat) -> bool;
uninterp spec fn g(x: nat) -> bool;
uninterp spec fn h(x: nat, y: nat) -> bool;and we use them in the following proof code:
proof fn trigger_forever2()
requires
forall|x: nat| g(x),
forall|x: nat, y: nat| h(x, y) == f(x, y),
forall|x: nat, y: nat| f(x + 1, 2 * y) && f(2 * x, y + x) || f(y, x) ==> #[trigger] f(x, y),
ensures
forall|x: nat, y: nat| x > 2318 && y < 100 ==> h(x, y),
{
assert(g(4));
}Notice that we have three quantifiers in the requires clause; the first will
trigger on g(x), which will be useful for proving the assertion about g(4).
The second quantifier triggers on both f(x, y) and h(x, y) and says that
they’re equal. The last quantifier is manually triggered on f(x, y), but it
then introduces two more expressions that have a similar shape, namely f(x + 1, 2 * y) and f(2 * x, y + x). Each of these has new arguments to f, so
this will cause quantifier 3 to trigger again, creating an infinite cycle of
instantations. Notice that each such instantiation will also cause quantifier
2 to trigger as well.
If we run Verus on this example, it will quickly time out. When this happens, you
can run Verus with the --profile option to launch the profiler. We strongly
recommend combining that option with --rlimit 1, so that you don’t generate too
much profiling data (the more you generate, the longer the analysis takes). With
--profile, if verification times out, the profiler automatically launches.
If you want to profile a function that is verifying successfully but slowly, you
can use the --profile-all option. You may want to combine this with the
--verify-function option to target the function you’re interested in.
If we run the profiler on the example above, we’ll see something along the lines of:
error: function body check: Resource limit (rlimit) exceeded
--> ../examples/trigger_loops.rs:66:7
|
66 | proof fn trigger_forever2()
| ^^^^^^^^^^^^^^^^^^^^^
note: Analyzing prover log for (profile rerun) trigger_loops::trigger_forever2 ...
Z3 4.12.5
note: Log analysis complete for (profile rerun) trigger_loops::trigger_forever2
note: Profile statistics for trigger_loops::trigger_forever2
note: Observed 17,963 total instantiations of user-level quantifiers
note: Cost * Instantiations: 2269911826 (Instantiated 8,981 times - 49% of the total, cost 252746) top 1 of 3 user-level quantifiers.
--> ../examples/trigger_loops.rs:70:93
|
70 | ... forall|x: nat, y: nat| f(x + 1, 2 * y) && f(2 * x, y + x) || f(y, x) ==> #[trigger] f(x, y),
| ------------------------------------------------------------------------------------^^^^^^^
| |
| Triggers selected for this quantifier
note: Cost * Instantiations: 397732566 (Instantiated 8,981 times - 49% of the total, cost 44286) top 2 of 3 user-level quantifiers.
--> ../examples/trigger_loops.rs:69:32
|
69 | forall|x: nat, y: nat| h(x, y) == f(x, y),
| -----------------------^^^^^^^----^^^^^^^
| |
| Triggers selected for this quantifier
note: Cost * Instantiations: 3 (Instantiated 1 times - 0% of the total, cost 3) top 3 of 3 user-level quantifiers.
--> ../examples/trigger_loops.rs:68:24
|
68 | forall|x: nat| g(x),
| ---------------^^^^
| |
| Triggers selected for this quantifier
verification results:: 0 verified, 1 errors
error: aborting due to 1 previous error
The profiler measures two aspects of quantifier performance. First, it collects a basic count of how
many times each quantifier is instantiated. Second, it attempts to calculate a “cost” for each
quantifier. The cost of a quantifier is the sum of cost of its instantiations. The cost of an instantiation i
is roughly 1 + sum_{(i, n) \in edges} cost(n) / in-degree(n) where each n is an instantiation caused
by instantiation i. In other words, instantiation i produced a term that caused the solver to create
another instantiation (of the same or a different quantifier) n. This heuristic attempts to place more
weight on quantifiers whose instantiations themselves cause other expensive instantiations. By default,
the profiler will sort by the product of these two metrics.
In the example above, we see that the top quantifier is quantifer 3 in the Verus code, which is indeed the troublemaker. The use of the cost metric elevates it above quantifier 2, which had the same number of instantiations but is really an “innocent bystander” in this scenario. And both of these quantifiers are instantiated vastly more than quantifier 3, indicating that quantifier 3 is not the source of the problem. If all of the quantifiers have a small number of instantiations, that may be a sign that quantifier instantiation is not the underlying source of the solver’s poor performance.
Modules, hiding, opaque, reveal
One possible cause for verification timeouts is unfolding a function definition that is especially complex, or contains problematic quantifiers.
To prevent automatic unfolding, you can use opaque to hide the body of the function from the verifier. You can then use reveal to selectively “reveal” the body of the function in places where you want the verifier to unfold its definition.
Here’s a small example of how to use opaque and reveal:
mod M1 {
use verus_builtin::*;
#[verifier::opaque]
spec fn min(x: int, y: int) -> int {
if x <= y {
x
} else {
y
}
}
fn test() {
assert(min(10, 20) == min(10, 20)); // succeeds
assert(min(10, 20) == 10); // FAILS
reveal(min);
assert(min(10, 20) <= 10); // succeeds
}
}This is very similar to closed spec functions discussed in the previous section! The main difference is that opaque and reveal are more flexible. opaque hides the function body even in the current module, so you can use reveal to selectively expose the function body in specific proof blocks.
In general, you want to use closed spec if you want to have the function body available in the current module, and you build proof functions about this specification in the same module. So you all you need outside the module is the public proof functions related to this spec function. Therefore open and closed spec function are well suited for abstraction, whereas opaque is a mechanism for controlling automation and verification performance, rather than modularity.
You can see more advanced use of hiding a function body in the reference.
Hiding local proofs with assert(...) by { ... }
Motivation
Sometimes, in a long function, you need to establish a fact F that requires
a modest-size proof P. Typically, you do this by ...; P; assert(F); ....
But doing this comes with a risk: the facts P introduces can be used not
only for proving F but also for proving the entire rest of the
function. This gives the SMT solver much more to think about when proving things beyond
assert(F), which is especially problematic when these additional facts are
universally quantified. This can make the solver take longer, and even time out, on
the rest of the function.
Enter assert(...) by { ... }
Saying assert(F) by {P} restricts the context that P affects, so that
it’s used to establish F and nothing else. After the closing brace at the
end of { P }, all facts that it established except for F are removed from
the proof context.
Underlying mechanism
The way this works internally is as follows. The solver is given the facts following
from P as a premise when proving F but isn’t given them for the rest of
the proof. For instance, suppose lemma_A establishes fact A and lemma_B
establishes fact B. Then
lemma_A();
assert(F) by { lemma_B(); };
assert(G);
is encoded to the solver as something like (A && B ==> F) && (A ==> G). If B is an expansive fact
to think about, like forall|i: int| b(i), the solver won’t be able to think about it
when trying to establish G.
Difference from auxiliary lemmas
Another way to isolate the proof of F from the local context is to put the
proof P in a separate lemma and invoke that lemma. To do this, the proof
writer has to think about what parts of the context (like fact A in the
example above) are necessary to establish F, and put those as requires
clauses in the lemma. The developer may then also need to pass other variables
to the lemma that are mentioned in those required facts. This can be done, but
can be a lot of work. Using assert(F) by { P } obviates all this work. It
also makes the proof more compact by removing the need to have a separate
lemma with its own signature.
Structured Proofs by Calculation
Motivation
Sometimes, you need to establish some relation R between two expressions, say,
a_1 and a_n, where it might be easier to do this in a series of steps, a_1
to a_2, a_2 to a_3, … all the way to a_n. One might do this by just
doing all the steps at once, but as mentioned in the section on
assert-by, a better approach might be to split it into a
collection of restricted contexts. This is better, but still might not be ideal,
since you need to repeat each of the intermediate expressions at each point.
calc!ulations, to Reduce Redundant Redundancy
The calc! macro supports structured proofs through calculations.
In particular, one can show a_1 R a_n for some transitive relation R by performing a series
of steps a_1 R a_2, a_2 R a_3, … a_{n-1} R a_n. The calc macro provides both convenient
syntax sugar to perform such a proof conveniently, without repeating oneself too often, or
exposing the internal steps to the outside context.
The expected usage looks like:
calc! {
(R)
a_1; { /* proof that a_1 R a_2 */ }
a_2; { /* proof that a_2 R a_3 */ }
...
a_n;
}For example,
let a: int = 2;
calc! {
(<=)
a; {}
a + 3; {}
5;
}which is equivalent to proving a <= 5 using a <= a + 3 <= 5. In this case, each
of the intermediate proofs are trivial, thus have an empty {} block, but in
general, can have arbitrary proofs inside their blocks.
Notice that you mention a_1, a_2, … a_n only once each. Additionally,
the proof for each of the steps is localized, and restricted to only its
particular step, ensuring that proof-context is not polluted.
The body of the function where this calc statement is written only gets to see
a_1 R a_n, and not any of the intermediate steps (or their proofs), further
limiting proof-context pollution.
Currently, the calc! macro supports common transitive relations for R (such
as == and <=). This set of relations may be extended in the future.
Using Different Relations for Intermediate Steps
While a relation like <= might be useful to use like above, it is possible
that not every intermediate step needs a <=; sometimes one might be able to be
more precise, and maintaining this (especially for documentation/readability
reasons) might be useful. For example, one might want to say a_1 <= a_2 == a_3 <= a_4 < a_5 <= ....
This is supported by calc by specifying the extra intermediate relations
inline (with the default being the top-level relation). These relations are
checked to be consistent with the top-level relation, to maintain
transitivity. So, for example, using > in the above chain would be caught
and reported with a helpful error message.
A simple example of using intermediate relations looks like the following:
let x: int = 2;
let y: int = 5;
calc! {
(<=)
x; (==) {}
5 - 3; (<) {}
5int; {} // Notice that no intermediate relation
// is specified here, so `calc!` will
// use the top-level relation, here `<=`.
y;
}This example is equivalent to saying x <= y using x == 5 - 3 < 5 <= y.
Proofs by Computation
Motivation
Some proofs should be “obvious” by simply computing on values. For example,
given a function pow(base, exp) defining exponentiation, we would like it to
be straightforward and deterministic to prove that pow(2, 8) == 256.
However, in general, to keep recursive functions like pow from overwhelming
the SMT solver with too many unrollings, Verus defaults to only unrolling such
definitions once. Hence, to make the assertion above go through, the developer
needs to carefully adjust the amount of “fuel” provided to unroll pow. Even
with such adjustment, we have observed cases where Z3 does “the wrong thing”,
e.g., it does not unroll the definitions enough, or it refuses to simplify
non-linear operations on statically known constants. As a result, seemingly
simple proofs like the one above don’t always go through as expected.
Enter Proof by Computation
Verus allows the developer to perform such proofs via computation, i.e.,
by running an internal interpreter over the asserted fact. The developer
can specify the desired computation using assert(e) by (compute) (for some
expression e). Continuing the example above, the developer could
write:
// Naive definition of exponentiation
spec fn pow(base: nat, exp: nat) -> nat
decreases exp,
{
if exp == 0 {
1
} else {
base * pow(base, (exp - 1) as nat)
}
}
proof fn concrete_pow() {
assert(pow(2, 8) == 256) by (compute); // Assertion 1
assert(pow(2, 9) == 512); // Assertion 2
assert(pow(2, 8) == 256) by (compute_only); // Assertion 3
}In Assertion 1, Verus will internally reduce the left-hand side to 256 by repeatedly evaluating
pow and then simplify the entire expression to true.
When encoded to the SMT solver, the result will be (approximately):
assert(true);
assume(pow(2, 8) == 256);
In other words, in the encoding, we assert whatever remains after
simplification and then assume the original expression. Hence, even if
simplification only partially succeeds, Z3 may still be able to complete the
proof. Furthermore, because we assume the original expression, it is still
available to trigger other ambient knowledge or contribute to subsequent facts.
Hence Assertion 2 will succeed, since Z3 will unfold the definition of pow
once and then use the previously established fact that pow(2,8) == 256.
If you want to ensure that the entire proof completes through computation and
leaves no additional work for Z3, then you can use assert(e) by (compute_only) as shown in Assertion 3. Such an assertion will fail unless
the interpreter succeeds in reducing the expression completely down to true.
This can be useful for ensuring the stability of your proof, since it does not
rely on any Z3 heuristics.
Important note: An assertion using proof by computation does not inherit any context from its environment. Hence, this example:
let x = 2;
assert(pow(2, x) == 4) by (compute_only);will fail, since x will be treated symbolically, and hence the assertion will
not simplify all the way down to true. This can be remedied either
by using assert(e) by (compute) and allowing Z3 to finish the proof, or by moving
the let into the assertion, e.g., as:
proof fn let_passes() {
assert({
let x = 2;
pow(2, x) == 4
}) by (compute_only);
}While proofs by computation are most useful for concrete values, the interpreter
also supports symbolic values, and hence it can complete certain proofs
symbolically. For example, given variables a, b, c, d, the following succeeds:
proof fn seq_example(a: Seq<int>, b: Seq<int>, c: Seq<int>, d: Seq<int>) {
assert(seq![a, b, c, d] =~= seq![a, b].add(seq![c, d])) by (compute_only);
}Many proofs by computation take place over a concrete range of integers. To reduce
the boilerplate needed for such proofs, you can use
all_spec.
In the example below,
use vstd::compute::RangeAll;
spec fn p(u: usize) -> bool {
u >> 8 == 0
}
proof fn range_property(u: usize)
requires 25 <= u < 100,
ensures p(u),
{
assert((25..100int).all_spec(|x| p(x as usize))) by (compute_only);
let prop = |x| p(x as usize);
assert(prop(u));
}we use all_spec to prove that p holds for all values between 25 and 100,
and hence it must hold for a generic value u that we know is in that range.
Note that all_spec currently expects to operate over ints, so you may need
add casts as appropriate. Also, due to some techinical restrictions, at present,
you can’t pass a top-level function like p to all_spec. Instead, you need
to wrap it in a closure, as seen in this example. Finally, the lemmas in vstd
will give you a quantified resulted about the outcome of all_spec, so you may
need to add an additional assertion (in our example, assert(prop(u))) to trigger
that quantifier. This guide provides more detail on quantifiers and
triggers in another chapter.
To prevent infinite interpretation loops (which can arise even when the code is
proven to terminate, since the termination proof only applies to concrete
inputs, whereas the interpreter may encounter symbolic values), Verus limits
the time it will spend interpreting any given proof by computation.
Specifically, the time limit is the number of seconds specified via the
--rlimit command-line option.
By default, the interpreter does not cache function call results based on the
value of the arguments passed to the function. Experiments showed this typically
hurts performance, since it entails traversing the (large) AST nodes representing
the arguments. However, some examples need such caching to succceed (e.g., computing
with the naive definition of Fibonacci). Such functions can be annotated with
#[verifier::memoize], which will cause their results to be cached during computation.
Current Limitations
- As mentioned above, the expression given to a proof by computation is interpreted in isolation from any surrounding context.
- The expression passed to a proof-by-computation assertion must be in spec mode, which means it cannot be used on proof or exec mode functions.
- The interpreter is recursive, so a deeply nested expression (or series of function calls) may cause Verus to exceed the process’ stack space.
See Also
- The test suite has a variety of small examples.
- We also have several more complex examples.
Breaking proofs into smaller pieces
Motivation
If you write a long function with a lot of proof code, Verus will correspondingly give the SMT solver a long and difficult problem to solve. So one can improve solver performance by breaking that function down into smaller pieces. This performance improvement can be dramatic because solver response time typically increases nonlinearly as proof size increases. After all, having twice as many facts in scope gives the solver far more than twice as many possible paths to search for a proof. As a consequence, breaking functions down can even make the difference between the solver timing out and the solver succeeding quickly.
Moving a subproof to a lemma
If you have a long function, look for a modest-size piece P of it that
functions as a proof of some locally useful set of facts S. Replace P with
a call to a lemma whose postconditions are S, then make P the body of that
lemma. Consider what parts of the original context of P are necessary to
establish S, and put those as requires clauses in the lemma. Those
requires clauses may involve local variables, in which case pass those
variables to the lemma as parameters.
For instance:
fn my_long_function(x: u64, ...)
{
let y: int = ...;
... // first part of proof, establishing fact f(x, y)
P1; // modest-size proof...
P2; // establishing...
P3; // facts s1 and s2...
P4; // about x and y
... // second part of proof, using facts s1 and s2
}
might become
proof fn my_long_function_helper(x: u64, y: int)
requires
f(x, y)
ensures
s1(x),
s2(x, y)
{
P1; // modest-size proof...
P2; // establishing...
P3; // facts s1 and s2...
P4; // about x and y
}
fn my_long_function(x: u64, ...)
{
... // first part of proof, establishing fact f(x, y)
my_long_function_helper(x, y);
... // second part of proof, using facts s1 and s2
}
You may find that, once you’ve moved P into the body of the lemma, you can
not only remove P from the long function but also remove significant
portions of P from the lemma where it was moved to. This is because a lemma
dedicated solely to establishing S will have a smaller context for the
solver to reason about. So less proof annotation may be necessary to get it to
successfully and quickly establish S. For instance:
proof fn my_long_function_helper(x: u64, y: int)
requires
f(x, y)
ensures
s1(x),
s2(x, y)
{
P1; // It turns out that P2 and P3 aren't necessary when
P4; // the solver is focused on just f, s1, s2, x, and y.
}
Dividing a proof into parts 1, 2, …, n
Another approach is to divide your large function’s proof into n consecutive
pieces and put each of those pieces into its own lemma. Make the first lemma’s
requires clauses be the requires clauses for the function, and make its
ensures clauses be a summary of what its proof establishes. Make the second
lemma’s requires clauses match the ensures clauses of the first lemma, and
make its ensures clauses be a summary of what it establishes. Keep going
until lemma number n, whose ensures clauses should be the ensures
clauses of the original function. Finally, replace the original function’s
proof with a sequence of calls to those n lemmas in order.
For instance:
proof fn my_long_function(x: u64)
requires r(x)
ensures e(x)
{
P1;
P2;
P3;
}
might become
proof fn my_long_function_part1(x: u64) -> (y: int)
requires
r(x)
ensures
mid1(x, y)
{
P1;
}
proof fn my_long_function_part2(x: u64, y: int)
requires
mid1(x, y)
ensures
mid2(x, y)
{
P2;
}
proof fn my_long_function_part3(x: u64, y: int)
requires
mid2(x, y)
ensures
e(x)
{
P3;
}
proof fn my_long_function(x: u64)
requires r(x)
ensures e(x)
{
let y = my_long_function_part1(x);
my_long_function_part2(x, y);
my_long_function_part3(x, y);
}
Since the expressions r(x), mid1(x, y), mid2(x, y), and e(x) are each
repeated twice, it may be helpful to factor each out as a spec function and
thereby avoid repetition.
Checklist: What to do when proofs go wrong
A proof is failing and I don’t expect it to. What’s going wrong?
- Try running Verus with
--expand-errorsto get more specific information about what’s failing. - Check Verus’s output for
recommends-failures and other notes. - Add more
assertstatements. This can either give you more information about what’s failing, or even just fix the proof. See this guide. - Are you using quantifiers? Make sure you understand how triggers work.
- Are you using nonlinear arithmetic? Try one of the strategies for nonlinear arithmetic.
- Are you using bitwise arithmetic or
as-truncation? Try the bit_vector solver. - Are you relying on the equality of a container type (like
SeqorMap)? Try extensional equality. - Are you using a recursive function? Make sure you understand how fuel works.
The verifier says “rlimit exceeded”. What can I do?
- Try the quantifier profiler to identify a problematic trigger-pattern.
- Try breaking the proof into pieces.
- Try increasing the
rlimit. Sometimes a proof really is just kind of big and you want Verus to spend a little more effort on it.
My proof is “flaky”: it sometimes works, but then I change something unrelated, and it breaks.
- Try adding
#[verifier::spinoff_prover]to the function. This can make it a little more stable. - Try breaking the proof into pieces.
Mutation, references, and borrowing
The cornerstone of Rust’s type system is its formulation of ownership, references, and borrowing. In this section, we’ll discuss how Verus handles these concepts.
Rust review
In short, ownership is Rust’s way of managing memory safely. Every piece of memory that is allocated and used in a Rust program has one owner. For example, when assigning 42 to the variable x, x is the owner of that particular numerical value. Owners can be variables, structs, inputs to functions, etc. Owners can change through an action called move — but, at any given time, a particular piece of memory can only have one owner. Finally, when a piece of memory’s owner goes out of scope, the piece of memory is no longer considered valid and cannot be accessed in the program.
Since it can often be cumbersome or expensive to transfer ownership and make copies of data, Rust also provides a reference system to allow access to data via pointers without obtaining full ownership. To maintain memory safety, Rust enforces several restrictions on their use: every memory location in a Rust program (e.g., stack variable, heap-allocated memory) will always, at any point in time, have either:
- No live references
- One or more immutable references (denoted by the type
&T) - Exactly one mutable reference (denoted by the type
&mut T)
As suggested by the name, immutable references only grant read-only access to a particular piece of memory, while mutable references grant write-access. However, even mutable references don’t have the same power as full ownership, for example, they cannot deallocate the memory being pointed to.
Though the system may seem restrictive, it has a number of compelling consequences, such as the enforcement of temporal memory safety and data-race-freedom. It also has signficant advantages for Verus, greatly simplifying the verification conditions needed to prove code correct.
Borrowing in Verus
Immutable borrows
Verus has full support for immutable borrows. These are the easiest to use, as Verus treats
them the same as non-references, e.g., to Verus, a &u32 is the same as a u32.
In nearly all situations, there is no need to reason about the pointer address.
fn immutable_references_example() {
let x: u32 = 0;
let y: u32 = 0;
let immut_ref_x = &x;
let immut_ref_y = &y;
assert(x == 0);
assert(*immut_ref_x == 0);
// These point to different stack variables, but they compare equal.
assert(immut_ref_x == immut_ref_y);
}Mutable borrows
Currently, Verus only supports the use of mutable references as arguments to a function, such as in the following example.
fn modify_y(a: &mut u32)
ensures *a == 2
{
*a = 2;
}
fn mutable_example()
{
let mut y: u32 = 1;
assert(y == 1);
modify_y(&mut y);
assert(y == 2);
}In the subsequent chapters, we’ll discuss more how to verify code with mutable references, e.g., how to write specifications on functions that take mutable arguments.
Lifetime variables
Rust’s type system sometimes requires the use of lifetime variables to check that borrows are used correctly (i.e., that they obey the mutual-exclusivity rules discussed above). Fortunately, these have essentially no impact on verification. Besides the lifetime checks that Rust always does, Verus ignores lifetime variables for the sake of theorem-proving.
Requires and ensures with mutable references
If a function takes a mutable reference, say x: &mut T, as an argument, then function specification
needs to be able to refer to two different value: the value behind the mutable reference
before the function executes, and the value after.
More specifically, the requires clause will need to refer to the pre-value,
while the ensures clause may need to refer to either (e.g., to specify how the value changes
over the course of the function).
- To refer to the pre-state, use
*old(x) - To refer to the post-state, use
*x.
(Note that this implies that in the requires clause, the mutable reference’s value can only
be referred to by using old.)
Example
The following example shows how we can use the requires clause to constraint the input value,
while the ensures clause relaets to the new value to the input value:
fn increment(a: &mut u32)
requires *old(a) < u32::MAX,
ensures *a == *old(a) + 1,
{
*a = *a + 1;
}
fn caller()
{
let mut z: u32 = 0;
increment(&mut z);
assert(z == 1);
}In the increment function call, *old(a) refers to the dereferenced value of the mutable reference a at the beginning of the function call and *a in the ensures clause refers to the dereferenced value of the mutable reference a at the end of the function call.
Assertions about mutable references
Assertions containing mutable references allow us to make statements about the prior (at the beginning of the function call) and current state of the piece of memory to which the mutable reference points. Consider the following example:
fn check_and_assert(a: &mut u32)
requires *old(a) == 0
{
assert(*old(a) == 0);
*a = *a + 1;
assert(*a == 1);
*a = *a + 1;
assert(*a == 2);
assert(*old(a) == 0);
}
fn asserts()
{
let mut x: u32 = 0;
check_and_assert(&mut x);
}In the check_and_assert function call, *old(a) refers to the dereferenced value of the mutable reference a at the beginning of the function call and *a refers to the current dereferenced value of the mutable reference a.
Below is a slightly more complicated example involving both assert, requires, and ensures:
fn decrease(b: &mut u32)
requires
*old(b) == 10,
ensures
*b == 0,
{
let mut i: u32 = 0;
while (*b > 0)
invariant
*b == (10 - i),
decreases *b,
{
*b = *b - 1;
i = i + 1;
assert(*b == (10 - i));
}
assert(*b == 0);
assert(*old(b) == 10);
}
fn complex_example()
{
let mut d: u32 = 10;
decrease(&mut d);
assert(d == 0);
}Higher-order executable functions
Here we discuss the use of higher order functions via closures and other function types in Rust.
Passing functions as values
In Rust, functions may be passed by value using the FnOnce, FnMut, and Fn traits.
Just like for normal functions, Verus supports reasoning about the preconditions
and postconditions of such functions.
Reasoning about preconditions and postconditions
Verus allows you to reason about the preconditions and postconditions of function values
via two builtin spec functions: call_requires and call_ensures.
call_requires(f, args)represents the precondition. It takes two arguments: the function object and arguments as a tuple. If it returns true, then it is possible to callfwith the given args.call_ensures(f, args, output)represents the postcondition. It takes takes three arguments: the function object, arguments, and return vaue. It represents the valid input-output pairs forf.
The vstd library also provides aliases, f.requires(args) and f.ensures(args, output).
These mean the same thing as call_requires and call_ensures.
As with any normal call, Verus demands that the precondition be satisfied when you call a function object. This is demonstrated by the following example:
fn double(x: u8) -> (res: u8)
requires
0 <= x < 128,
ensures
res == 2 * x,
{
2 * x
}
fn higher_order_fn(f: impl Fn(u8) -> u8) -> (res: u8) {
f(50)
}
fn test() {
higher_order_fn(double);
}As we can see, test calls higher_order_fn, passing in double.
The higher_order_fn then calls the argument with 50. This should be allowed,
according to the requires clause of double; however, higher_order_fn does not have
the information to know this is correct.
Verus gives an error:
error: Call to non-static function fails to satisfy `callee.requires(args)`
--> vec_map.rs:25:5
|
25 | f(50)
| ^^^^^
To fix this, we can add a precondition to higher_order_fn that gives information on
the precondition of f:
fn double(x: u8) -> (res: u8)
requires
0 <= x < 128,
ensures
res == 2 * x,
{
2 * x
}
fn higher_order_fn(f: impl Fn(u8) -> u8) -> (res: u8)
requires
call_requires(f, (50,)),
{
f(50)
}
fn test() {
higher_order_fn(double);
}The (50,) looks a little funky. This is a 1-tuple.
The call_requires and call_ensures always take tuple arguments for the “args”.
If f takes 0 arguments, then call_requires takes a unit tuple;
if f takes 2 arguments, then it takes a pair; etc.
Here, f takes 1 argument, so it takes a 1-tuple, which can be constructed by using
the trailing comma, as in (50,).
Verus now accepts this code, as the precondition of higher_order_fn now guarantees that
f accepts the input of 50.
We can go further and allow higher_order_fn to reason about the output value of f:
fn double(x: u8) -> (res: u8)
requires
0 <= x < 128,
ensures
res == 2 * x,
{
2 * x
}
fn higher_order_fn(f: impl Fn(u8) -> u8) -> (res: u8)
requires
call_requires(f, (50,)),
forall|x, y| call_ensures(f, x, y) ==> y % 2 == 0,
ensures
res % 2 == 0,
{
let ret = f(50);
return ret;
}
fn test() {
higher_order_fn(double);
}Observe that the precondition of higher_order_fn places a constraint on the postcondition
of f.
As a result, higher_order_fn learns information about the return value of f(50).
Specifically, it learns that call_ensures(f, (50,), ret) holds, which by higher_order_fn’s
precondition, implies that ret % 2 == 0.
An important note
The above examples show the idiomatic way to constrain the preconditions and postconditions
of a function argument. Observe that call_requires is used in a positive position,
i.e., “call_requires holds for this value”.
Meanwhile call_ensures is used in a negative position, i.e., on the left hand side
of an implication: “if call_ensures holds for a given value, this is satisfies this particular constraint”.
It is very common to need a guarantee that f(args) will return one specific value,
say expected_return_value.
In this situation, it can be tempting to write,
requires call_ensures(f, args, expected_return_value),as your constraint. However, this is almost never what you actually want,
and in fact, Verus may not even let you prove it.
The proposition call_ensures(f, args, expected_return_value)
says that expected_return_value is a possible return value of f(args);
however, it says nothing about other possible return values.
In general, f may be nondeterministic!
Just because expected_return_value is one possible return
value does not mean it is only one.
When faced with this situation, what you really want is to write:
requires forall |ret| call_ensures(f, args, ret) ==> ret == expected_return_valueThis is the proposition that you really want, i.e., “if f(args) returns a value ret,
then that value is equal to expected_return_value”.
Of course, this is flipped around when you write a postcondition, as we’ll see in the next example.
Example: vec_map
Let’s take what we learned and write a simple function, vec_map, which applies a given
function to each element of a vector and returns a new vector.
The key challenge is to determine the right specfication to use.
The signature we want is:
fn vec_map<T, U>(v: &Vec<T>, f: impl Fn(T) -> U) -> (result: Vec<U>) where
T: Copy,First, what do we need to require? We need to require that it’s okay to call f
with any element of the vector as input.
requires
forall|i|
0 <= i < v.len() ==> call_requires(
f,
(v[i],),
),Next, what ought we to ensure? Naturally, we want the returned vector to have the same
length as the input. Furthermore, we want to guarantee that any element in the output
vector is a possible output when the provided function f is called on the corresponding
element from the input vector.
ensures
result.len() == v.len(),
forall|i|
0 <= i < v.len() ==> call_ensures(
f,
(v[i],),
#[trigger] result[i],
)
,Now that we have a specification, the implementation and loop invariant should fall into place:
fn vec_map<T, U>(v: &Vec<T>, f: impl Fn(T) -> U) -> (result: Vec<U>) where
T: Copy,
requires
forall|i|
0 <= i < v.len() ==> call_requires(
f,
(v[i],),
),
ensures
result.len() == v.len(),
forall|i|
0 <= i < v.len() ==> call_ensures(
f,
(v[i],),
#[trigger] result[i],
)
,
{
let mut result = Vec::new();
let mut j = 0;
while j < v.len()
invariant
forall|i| 0 <= i < v.len() ==> call_requires(f, (v[i],)),
0 <= j <= v.len(),
j == result.len(),
forall|i| 0 <= i < j ==> call_ensures(f, (v[i],), #[trigger] result[i]),
{
result.push(f(v[j]));
j += 1;
}
result
}Finally, we can try it out with an example:
fn double(x: u8) -> (res: u8)
requires
0 <= x < 128,
ensures
res == 2 * x,
{
2 * x
}
fn test_vec_map() {
let mut v = Vec::new();
v.push(0);
v.push(10);
v.push(20);
let w = vec_map(&v, double);
assert(w[2] == 40);
}Conclusion
In this chapter, we learned how to write higher-order functions with higher-order specifications, i.e., specifications that constrain the specifications of functions that are passed around as values.
All of the examples from this chapter passed functions by referring to them directly by name,
e.g., passing the function double by writing double.
In Rust, a more common way to work with higher-order functions is to pass closures.
In the next chapter, we’ll learn how to use closures.
Closures
In the previous chapter, we saw how to pass functions as values, which we did by referencing function items by name. However, it is more common in Rust to creating functions using closures.
Preconditions and postconditions on a closure
Verus allows you to specify requires and ensures on a closure just like you can for
any other function.
Here’s an example, calling the vec_map function we defined in the
previous chapter:
fn test_vec_map_with_closure() {
let double = |x: u8| -> (res: u8)
requires 0 <= x < 128
ensures res == 2 * x
{
2 * x
};
assert(forall |x| 0 <= x < 128 ==> call_requires(double, (x,)));
assert(forall |x, y| call_ensures(double, (x,), y) ==> y == 2 * x);
let mut v = Vec::new();
v.push(0);
v.push(10);
v.push(20);
let w = vec_map(&v, double);
assert(w[2] == 40);
}Closure capturing
One of the most challenging aspects of closures, in general, is that closures
can capture variables from the surrounding context.
Rust resolves this challenge through its hierarcy of function traits:
FnOnce, FnMut, and Fn.
The declaration of the closure and the details of its context capture determine
which traits it has. In turn,
the traits determine what capabilities the caller has: Can they call it more than
once? Can they call it in parallel?
See the Rust documentation for a more detailed introduction.
In brief, the traits provide the following capabilities to callers and restrictions on the context capture:
| Caller capability | Capturing | |
|---|---|---|
FnOnce | May call once | May move variables from the context |
FnMut | May call multiple times via &mut reference | May borrow mutably from the context |
Fn | May call multiple times via & reference | May borrow immutably from the context |
Verus does not yet support borrowing mutably from the context,
though it does handle moving and immutable borrows easily.
Therefore, Verus has better support for Fn and FnOnce—it does not yet take advantage of the
capturing capabilities supported by Rust’s FnMut.
Fortunately, both move-captures and immutable-reference-captures are easy to handle, as we can simply take their values inside the closure to be whatever they are at the program point of the closure expression.
Example:
fn example_closure_capture() {
let x: u8 = 20;
let f = || {
// Inside the closure, we have seamless access to
// variables defined outside the closure.
assert(x == 20);
x
};
}Strings
Verus supports reasoning about Rust String and &str:
fn get_char() {
let x = "hello world";
proof {
reveal_strlit("hello world");
}
assert(x@.len() == 11);
let val = x.get_char(0);
assert('h' === val);
}By default a string literal is treated as opaque,
fn opaque_by_default() {
let x = "hello world";
assert(x@.len() == 11); // FAILS
}this code results in a failed assertion:
error: assertion failed
--> ../examples/guide/strings.rs:21:12
|
21 | assert(x@.len() == 11); // FAILS
| ^^^^^^^^^^^^^^ assertion failed
which can be fixed by using reveal_strlit (like in the
example at the top).
However, comparing for equality does not require revealing literals:
fn literal_eq() {
let x = "hello world";
let y = "hello world";
assert(x@ == y@);
}A string literal is a &str and its view is a Seq<char>,
fn str_view() {
let x = "hello world";
let ghost y: Seq<char> = x@;
}whose value is unkown until the literal is revealed.
One can of course specify information about the view in, e.g., a function precondition (or some other predicate);
fn subrange<'a>(s: &str)
requires
s@ =~= "Hello"@,
{
assert(s@.subrange(0, 1) == "H"@);
}however, we need to reveal both literals to obtain information about their views in this case:
fn subrange<'a>(s: &str)
requires s@ =~= "Hello"@,
{
proof {
reveal_strlit("Hello");
reveal_strlit("H");
}
assert(s@.subrange(0, 1) =~= "H"@);
}Operating on strings currently requires the operations defined in vstd::strings documented here.
An important predicate for &str and String is is_ascii,
which enables efficient slicing, for example:
fn test() {
let a = String::from_str(("ABC"));
proof {
reveal_strlit("ABC");
}
assert(a.is_ascii());
let b = a.as_str().substring_ascii(2, 3);
proof {
reveal_strlit("C");
}
assert(b@ =~= ("C")@);
}
Unsafe code & complex ownership
Here we discuss the handling of more complex patterns relating to Rust ownership including:
- Interior mutability, where Rust allows you to mutate data even through a shared reference
&T - Raw pointers, which require proper ownership handling in order to uphold safety contracts
- Concurrency, where objects owned across different threads may need to coordinate.
Interior Mutability
The Interior Mutability pattern
is a particular Rust pattern wherein the user is able to manipulate the contents of a value
accessed via a shared borrow &. (Though & is often referred to as “immutable borrow,”
we will call it a “shared borrow” here, to avoid confusion.)
Two common Rust types illustrating interior mutability are
Cell and RefCell.
Here, we will overview the equivalent concepts in Verus.
Mutating stuff that can’t mutate
To understand the key challenge in verifying these interior mutability patterns,
recall an important fact of Verus’s SMT encoding. Verus assumes that any value of type &T,
for any type T, can never change. However, we also know that the contents of a
&Cell<V> might change. After all, that’s the whole point of the Cell<T> type!
The inescapable conclusion, then, is that
the value taken by a Cell<T> in Verus’ SMT encoding must not depend on the cell’s contents.
Instead, the SMT “value” of a Cell<T> is nothing more than a unique identifier for the Cell.
In some regards, it may help to think of Cell<T> as similar to a pointer T*.
The value of the Cell<T> is only its identifier (its “pointer address”) rather than
its contents (“the thing pointed to be a pointer”). Of course, it’s not a pointer, but
from the perspective of the encoding, it might as well be.
Note one immediate ramification of this property:
Verus’ pure equality === on Cell types cannot possibly
give the same results as Rust’s standard == (eq) on Cell types.
Rust’s == function actually compares the contents of the cells.
But pure equality, ===, which must depend on the SMT encoding values,
cannot possibly depend on the contents!
Instead, === compares two cells as equal only if they are the same cell.
So, with these challenges in mind, how do we handle interior mutability in Verus?
There are a few different approaches we can take.
-
When retrieving a value from the interior of a Cell-like data structure, we can model this as non-deterministically receiving a value of the given type. At first, this might seem like it gives us too little to work with for verifying correctness properties. However, we can impose additional structure by specifying data invariants to restrict the space of possible values.
-
Track the exact value using
tracked ghostcode.
More sophisticated data structures—especially concurrent ones—often require a careful balance of both approaches. We’ll introduce both here.
Data Invariants with InvCell.
Suppose we have an expensive computation and we want to memoize its value. The first time
we need to compute the value, we perform the computation and store its value for whenever
it’s needed later. To do this, we’ll use a Cell, whose interior is intialized to None
to store the computed value.
The memoized compute function will then:
- Read the value in the
Cell.- If it’s
None, then the value hasn’t been computed yet. Compute the value, store it for later, then return it. - If it’s
Some(x), then the value has already been computed, so return it immediately.
- If it’s
Crucially, the correctness of this approach doesn’t actually depend on being able to predict which of these cases any invocation will take. (It might be a different story if we were attempting to prove a bound on the time the program will take.) All we need to know is that it will take one of these cases. Therefore, we can verify this code by using a cell with a data invariant:
- Invariant: the value stored in the interior of the cell is either
NoneorSome(x), wherexis the expected result of the computation.
Concretely, the above can be implemented in Verus using
InvCell,
provided by Verus’ standard library, which provides a data-invariant-based specification.
When constructing a new InvCell<T>, the user specifies a data invariant: some boolean predicate
over the type T which tells the cell what values are allowed to be stored.
Then, the InvCell only has to impose the restriction that whenever the user writes to the cell,
the value val being written has to satisfy the predicate, cell.inv(val).
In exchange, though, whenever the user reads from the cell, they know the value they
receive satisfies cell.inv(val).
Here’s an example using an InvCell to implement a memoized function:
spec fn result_of_computation() -> u64 {
2
}
fn expensive_computation() -> (res: u64)
ensures
res == result_of_computation(),
{
1 + 1
}
spec fn cell_is_valid(cell: &InvCell<Option<u64>>) -> bool {
forall|v|
(cell.inv(v) <==> match v {
Option::Some(i) => i == result_of_computation(),
Option::None => true,
})
}
// Memoize the call to `expensive_computation()`.
// The argument here is an InvCell wrapping an Option<u64>,
// which is initially None, but then it is set to the correct
// answer once it's computed.
//
// The precondition here, given in the definition of `cell_is_valid` above,
// says that the InvCell has an invariant that the interior contents is either
// `None` or `Some(i)` where `i` is the desired value.
fn memoized_computation(cell: &InvCell<Option<u64>>) -> (res: u64)
requires
cell_is_valid(cell),
ensures
res == result_of_computation(),
{
let c = cell.get();
match c {
Option::Some(i) => {
// The value has already been computed; return the cached value
i
},
Option::None => {
// The value hasn't been computed yet. Compute it here
let i = expensive_computation();
// Store it for later
cell.replace(Option::Some(i));
// And return it now
i
},
}
}Tracked ghost state with PCell.
(TODO finish writing this chapter)
Pointers and cells
See the vstd documentation for more information on handling these features.
- For cells, see
PCell - For pointers to fixed-sized heap allocations, see
PPtr. - For general support for
*mut Tand*const T, seevstd::raw_ptr
Concurrency
Verus provides the VerusSync framework for verifing programs that require a nontrivial ownership discipline. This includes multi-threaded concurrent code, and frequently it is also needed for nontrivial applications of unsafe features (such as pointers or unsafe cells).
The topic is sufficiently complex that we cover it in a separate tutorial and reference book.
Verifying a container library
In this section, we’ll learn how to verify a simple container library, specifically, via an example of a map data structure implemented using a binary search tree. In the case study, we’ll explore various considerations for writing a modular specification that encapsulates verification details as well as implementation details.
A simple binary search tree
In this section, we’re going to be implementing and verifying a Binary Search Tree (BST).
In the study of data structures, there are many known ways to balance a binary search tree. To keep things simple, we won’t be implementing any of them—instead, we’ll be implementing a straightforward, unbalanced binary search tree. Improving the design to be more efficient will be left as an exercise.
Furthermore, our first draft of an implementation is going to map keys
of the fixed orderable type, u64, to values of type V. In a later chapter,
we’ll change the keys to also be generic, thus mapping K to V for arbitrary types
K and V.
The implementation
The structs
We’ll start by defining the tree shape itself, which contains one (key, value) pair at every node. We make no distinction between “leaf nodes” and “interior nodes”. Rather, every node has an optional left child and an optional right child. Furthermore, the tree might be entirely empty, in which case there is no root.
struct Node<V> {
key: u64,
value: V,
left: Option<Box<Node<V>>>,
right: Option<Box<Node<V>>>,
}
pub struct TreeMap<V> {
root: Option<Box<Node<V>>>,
}Note that only TreeMap is marked pub. Its field, root, as well as the Node type
as a whole, are implementation details, and thus are private to the module.
The abstract view
When creating a new data structure, there are usually two important first steps:
- Establish an interpretation of the data structure as some abstract datatype that will be used to write specifications.
- Establish the well-formedness invariants of the data structure.
We’ll do the first one first (in part because it will actually help with the second one).
In this case, we want to interpret the data structure as a
Map<u64, V>.
We can define such a function recursively.
impl<V> Node<V> {
spec fn optional_as_map(node_opt: Option<Box<Node<V>>>) -> Map<u64, V>
decreases node_opt,
{
match node_opt {
None => Map::empty(),
Some(node) => node.as_map(),
}
}
spec fn as_map(self) -> Map<u64, V>
decreases self,
{
Node::<V>::optional_as_map(self.left)
.union_prefer_right(Node::<V>::optional_as_map(self.right))
.insert(self.key, self.value)
}
}
impl<V> TreeMap<V> {
pub closed spec fn as_map(self) -> Map<u64, V> {
Node::<V>::optional_as_map(self.root)
}
}Again note that only TreeMap::as_map is marked pub, and furthermore, that it’s marked
closed. The definition of as_map is, again, an implementation detail.
It is customary to also implement the
View trait
as a convenience. This lets clients refer to the map implementation using the @ notation,
e.g., tree_map@ as a shorthand for tree_map.view().
We’ll be writing our specifications in terms of tree_map.view().
impl<V> View for TreeMap<V> {
type V = Map<u64, V>;
open spec fn view(&self) -> Map<u64, V> {
self.as_map()
}
}Establishing well-formedness
Next we establish well-formedness. This amounts to upholding the BST ordering property,
namely, that for every node N, the nodes in N’s left subtree have keys less than
N, while the nodes in N’s right subtree have keys greater than N.
Again, this can be defined by a recursive spec function.
impl<V> Node<V> {
spec fn well_formed(self) -> bool
decreases self,
{
&&& (forall |elem| Node::<V>::optional_as_map(self.left).dom().contains(elem) ==> elem < self.key)
&&& (forall |elem| Node::<V>::optional_as_map(self.right).dom().contains(elem) ==> elem > self.key)
&&& (match self.left {
Some(left_node) => left_node.well_formed(),
None => true,
})
&&& (match self.right {
Some(right_node) => right_node.well_formed(),
None => true,
})
}
}
impl<V> TreeMap<V> {
pub closed spec fn well_formed(self) -> bool {
match self.root {
Some(node) => node.well_formed(),
None => true, // empty tree always well-formed
}
}
}Implementing a constructor: TreeMap::new()
Defining a constructor is simple; we create an empty tree with no root. The specification indicates that the returned object must represent the empty map.
impl<V> TreeMap<V> {
pub fn new() -> (tree_map: Self)
ensures
tree_map.well_formed(),
tree_map@ == Map::<u64, V>::empty(),
{
TreeMap::<V> { root: None }
}
}Recall that tree_map@ is equivalent to tree_map.as_map().
An inspection of the definition of tree_map.as_map() and Node::optional_as_map() should
make it apparent this will be the empty map when root is None.
Observe again that this specification does not refer to the tree internals at all, only that it is well-formed and that its abstract view is the empty map.
Implementing the insert operation
We can also implement insert using a recursive traversal. We search for the given node,
using the well-formedness conditions to prove that we’re doing the right thing.
During this traversal, we’ll either find a node with the right key, in which case we update
the value, or we’ll reach a leaf without ever finding the desired node, in which case we
create a new node.
(Aside: One slight snag has to do with a limitation of Verus’s handing of mutable references.
Specifically, Verus doesn’t yet support an easy way to get a
&mut T out of a &mut Option<T>. To get around this, we use Option::take to get ownership of the node.)
impl<V> Node<V> {
fn insert_into_optional(node: &mut Option<Box<Node<V>>>, key: u64, value: V)
requires
old(node).is_some() ==> old(node).unwrap().well_formed(),
ensures
node.is_some() ==> node.unwrap().well_formed(),
Node::<V>::optional_as_map(*node) =~= Node::<V>::optional_as_map(*old(node)).insert(key, value),
decreases *old(node),
{
match node.take() {
None => {
*node = Some(Box::new(Node::<V> {
key: key,
value: value,
left: None,
right: None,
}));
}
Some(mut boxed_node) => {
(&mut *boxed_node).insert(key, value);
*node = Some(boxed_node);
}
}
}
fn insert(&mut self, key: u64, value: V)
requires
old(self).well_formed(),
ensures
self.well_formed(),
self.as_map() =~= old(self).as_map().insert(key, value),
decreases *old(self),
{
if key == self.key {
self.value = value;
assert(!Node::<V>::optional_as_map(self.left).dom().contains(key));
assert(!Node::<V>::optional_as_map(self.right).dom().contains(key));
} else if key < self.key {
Self::insert_into_optional(&mut self.left, key, value);
assert(!Node::<V>::optional_as_map(self.right).dom().contains(key));
} else {
Self::insert_into_optional(&mut self.right, key, value);
assert(!Node::<V>::optional_as_map(self.left).dom().contains(key));
}
}
}
impl<V> TreeMap<V> {
pub fn insert(&mut self, key: u64, value: V)
requires
old(self).well_formed(),
ensures
self.well_formed(),
self@ == old(self)@.insert(key, value),
{
Node::<V>::insert_into_optional(&mut self.root, key, value);
}
}Observe that the specification of TreeMap::insert is given in terms of
Map::insert.
Implementing the delete operation
Implementing delete is a little harder, because if we need to remove an interior node,
we might have to reshape the tree a bit. However, since we aren’t trying to follow
any particular balancing strategy, it’s still not that bad:
impl<V> Node<V> {
fn delete_from_optional(node: &mut Option<Box<Node<V>>>, key: u64)
requires
old(node).is_some() ==> old(node).unwrap().well_formed(),
ensures
node.is_some() ==> node.unwrap().well_formed(),
Node::<V>::optional_as_map(*node) =~= Node::<V>::optional_as_map(*old(node)).remove(key),
decreases *old(node),
{
if let Some(mut boxed_node) = node.take() {
if key == boxed_node.key {
assert(!Node::<V>::optional_as_map(boxed_node.left).dom().contains(key));
assert(!Node::<V>::optional_as_map(boxed_node.right).dom().contains(key));
if boxed_node.left.is_none() {
*node = boxed_node.right;
} else {
if boxed_node.right.is_none() {
*node = boxed_node.left;
} else {
let (popped_key, popped_value) = Node::<V>::delete_rightmost(&mut boxed_node.left);
boxed_node.key = popped_key;
boxed_node.value = popped_value;
*node = Some(boxed_node);
}
}
} else if key < boxed_node.key {
assert(!Node::<V>::optional_as_map(boxed_node.right).dom().contains(key));
Node::<V>::delete_from_optional(&mut boxed_node.left, key);
*node = Some(boxed_node);
} else {
assert(!Node::<V>::optional_as_map(boxed_node.left).dom().contains(key));
Node::<V>::delete_from_optional(&mut boxed_node.right, key);
*node = Some(boxed_node);
}
}
}
fn delete_rightmost(node: &mut Option<Box<Node<V>>>) -> (popped: (u64, V))
requires
old(node).is_some(),
old(node).unwrap().well_formed(),
ensures
node.is_some() ==> node.unwrap().well_formed(),
Node::<V>::optional_as_map(*node) =~= Node::<V>::optional_as_map(*old(node)).remove(popped.0),
Node::<V>::optional_as_map(*old(node)).dom().contains(popped.0),
Node::<V>::optional_as_map(*old(node))[popped.0] == popped.1,
forall |elem| Node::<V>::optional_as_map(*old(node)).dom().contains(elem) ==> popped.0 >= elem,
decreases *old(node),
{
let mut boxed_node = node.take().unwrap();
if boxed_node.right.is_none() {
*node = boxed_node.left;
assert(Node::<V>::optional_as_map(boxed_node.right) =~= Map::empty());
assert(!Node::<V>::optional_as_map(boxed_node.left).dom().contains(boxed_node.key));
return (boxed_node.key, boxed_node.value);
} else {
let (popped_key, popped_value) = Node::<V>::delete_rightmost(&mut boxed_node.right);
assert(!Node::<V>::optional_as_map(boxed_node.left).dom().contains(popped_key));
*node = Some(boxed_node);
return (popped_key, popped_value);
}
}
}
impl<V> TreeMap<V> {
pub fn delete(&mut self, key: u64)
requires
old(self).well_formed(),
ensures
self.well_formed(),
self@ == old(self)@.remove(key),
{
Node::<V>::delete_from_optional(&mut self.root, key);
}
}Observe that the specification of TreeMap::delete is given in terms of
Map::remove.
Implementing the get operation
Finally, we implement and verify TreeMap::get.
This function looks up a key and returns an Option<&V> (None if the key isn’t in the
TreeMap).
impl<V> Node<V> {
fn get_from_optional(node: &Option<Box<Node<V>>>, key: u64) -> Option<&V>
requires
node.is_some() ==> node.unwrap().well_formed(),
returns
(match node {
Some(node) => (if node.as_map().dom().contains(key) { Some(&node.as_map()[key]) } else { None }),
None => None,
}),
decreases node,
{
match node {
None => None,
Some(node) => {
node.get(key)
}
}
}
fn get(&self, key: u64) -> Option<&V>
requires
self.well_formed(),
returns
(if self.as_map().dom().contains(key) { Some(&self.as_map()[key]) } else { None }),
decreases self,
{
if key == self.key {
Some(&self.value)
} else if key < self.key {
proof { assert(!Node::<V>::optional_as_map(self.right).dom().contains(key)); }
Self::get_from_optional(&self.left, key)
} else {
proof { assert(!Node::<V>::optional_as_map(self.left).dom().contains(key)); }
Self::get_from_optional(&self.right, key)
}
}
}
impl<V> TreeMap<V> {
pub fn get(&self, key: u64) -> Option<&V>
requires
self.well_formed(),
returns
(if self@.dom().contains(key) { Some(&self@[key]) } else { None }),
{
Node::<V>::get_from_optional(&self.root, key)
}
}Using the TreeMap as a client
A short client program illustrates how we can reason about the TreeMap as if it were
a Map.
fn test() {
let mut tree_map = TreeMap::<bool>::new();
tree_map.insert(17, false);
tree_map.insert(18, false);
tree_map.insert(17, true);
assert(tree_map@ == map![17u64 => true, 18u64 => false]);
tree_map.delete(17);
assert(tree_map@ == map![18u64 => false]);
let elem17 = tree_map.get(17);
let elem18 = tree_map.get(18);
assert(elem17.is_none());
assert(elem18 == Some(&false));
}Full source
The full source for this example can be found here.
Encapsulating well-formedness with type invariants
Recall our specifications from the previous chapter:
impl<V> TreeMap<V> {
pub fn new() -> (tree_map: Self)
ensures
tree_map.well_formed(),
tree_map@ == Map::<u64, V>::empty(),
pub fn insert(&mut self, key: u64, value: V)
requires
old(self).well_formed(),
ensures
self.well_formed(),
self@ == old(self)@.insert(key, value),
pub fn delete(&mut self, key: u64)
requires
old(self).well_formed(),
ensures
self.well_formed(),
self@ == old(self)@.remove(key),
pub fn get(&self, key: u64) -> Option<&V>
requires
self.well_formed(),
returns
(if self@.dom().contains(key) { Some(&self@[key]) } else { None }),
}Observe the presenence of this tree_map.well_formed() predicate, especially in the
requires clauses.
As a result of this,
the client needs to work with this tree_map.well_formed() predicate all throughout
their own code. For example:
fn test2() {
let mut tree_map = TreeMap::<bool>::new();
test_callee(tree_map);
}
fn test_callee(tree_map: TreeMap<bool>)
requires
tree_map.well_formed(),
{
let mut tree_map = tree_map;
tree_map.insert(25, true);
tree_map.insert(100, true);
}Without the requires clause, the above snippet would fail to verify.
Intuitively, however, one might wonder why we have to carry this predicate around at all.
After all,
due to encapsulation, it isn’t ever possible for the client to create a tree_map where
well_formed() doesn’t hold.
In this section, we’ll show how to use Verus’s type invariants feature to remedy this burden from the client.
Applying the type_invariant attribute.
In order to tell Verus that we want the well_formed() predicate to be inferred
automatically, we can mark it with the #[verifier::type_invariant] attribute:
impl<V> TreeMap<V> {
#[verifier::type_invariant]
spec fn well_formed(self) -> bool {
match self.root {
Some(node) => node.well_formed(),
None => true, // empty tree always well-formed
}
}
}This has two effects:
- It adds an extra constraint that all
TreeMapobjects satsify thewell_formed()condition at all times. This constraint is checked by Verus whenever aTreeMapobject is constructed or modified. - It allows the programmer to assume the
well_formed()condition at all times, even when it isn’t present in arequiresclause.
Note that in addition to adding the type_invariant attribute, we have also removed
the pub specifier from well_formed.
Now not only is the body invisible to the client, even the name is as well.
After all, our intent is to prevent the client from needing to reason about it, at which point
there is no reason to expose it through the public interface at all.
Of course, for this to be possible, we’ll need to update the specifications of TreeMap’s
various pub methods.
Updating the code: new
Let’s start with an easy one: new.
impl<V> TreeMap<V> {
pub fn new() -> (s: Self)
ensures
s@ == Map::<u64, V>::empty()
{
TreeMap::<V> { root: None }
}
}All we’ve done here is remove the s.well_formed() postcondition, which as discussed,
is no longer necessary.
Crucially, Verus still requires us to prove that s.well_formed() holds.
Specifically, since well_formed has been marked with #[verifier::type_invariant],
Verus checks that well_formed() holds when the TreeMap constructor returns.
As before, Verus can check this condition fairly trivially.
Updating the code: get
Now let’s take a look at get. The first thing to notice is that we remove
the requires self.well_formed() clause.
impl<V> TreeMap<V> {
pub fn get(&self, key: u64) -> Option<&V>
returns
(if self@.dom().contains(key) { Some(&self@[key]) } else { None }),
{
proof { use_type_invariant(&*self); }
Node::<V>::get_from_optional(&self.root, key)
}
}Given that we no longer have the precondition, how do we deduce self.well_formed()
(which is needed to prove self.root is well-formed and call Node::get_from_optional)?
This can be done with the built-in pseudo-lemma use_type_invariant. When called on any object,
this feature guarantees that the provided object satisfies its type invariants.
Updating the code: insert
Now let’s check TreeMap::insert, which if you recall, has to modify the tree.
impl<V> TreeMap<V> {
pub fn insert(&mut self, key: u64, value: V)
ensures
self@ == old(self)@.insert(key, value),
{
proof { use_type_invariant(&*self); }
let mut root = None;
std::mem::swap(&mut root, &mut self.root);
Node::<V>::insert_into_optional(&mut root, key, value);
self.root = root;
}
}As before, we use use_type_invariant to establish that self.well_formed() holds at the
beginning of the function, even without the requires clause.
One slight challenge that arises from the use of #[verifier::type_invariant] is that it
enforces type invariants to hold at every program point. Sometimes, this can make
intermediate computation a little tricky.
In this case, an easy way to get around this is to swap the root field with None, then swap back when we’re done.
This works because the empty TreeMap trivially satisfies the well-formedness, so it’s allowed.
One might wonder why we can’t just do
Node::<V>::insert_into_optional(&mut self.root, key, value)
without swapping. The trouble with this is that it requires us to ensure the call
to insert_into_optional is “unwind-safe”, i.e., that all type invariants would be preserved
even if a panic occurs and insert_into_optional has to exit early. Right now, Verus only
has one way to ensure unwind-safety, which is to bluntly ensure that no unwinding happens
at all.
Thus, the ideal solution would be to mark insert_into_optional
as no_unwind. However, this is impossible in this case, because
node insertion will call Box::new.
Between this problem, and Verus’s current limitations regarding unwind-safety, the
swap approach becomes the easiest solution as a way of sidestepping it.
Check the reference page for more information on
the limitations of the type_invariant feature.
Updating the code: delete
This is pretty much the same as insert.
impl<V> TreeMap<V> {
pub fn delete(&mut self, key: u64)
ensures
self@ == old(self)@.remove(key),
{
proof { use_type_invariant(&*self); }
let mut root = None;
std::mem::swap(&mut root, &mut self.root);
Node::<V>::delete_from_optional(&mut root, key);
self.root = root;
}
}The new signatures and specifications
Putting it all together, we end up with the following specifications for our public API:
impl<V> TreeMap<V> {
pub fn new() -> (s: Self)
ensures
s@ == Map::<u64, V>::empty()
pub fn insert(&mut self, key: u64, value: V)
ensures
self@ == old(self)@.insert(key, value),
pub fn delete(&mut self, key: u64)
ensures
self@ == old(self)@.remove(key),
pub fn get(&self, key: u64) -> Option<&V>
returns
(if self@.dom().contains(key) { Some(&self@[key]) } else { None }),
}These are almost the same as what we had before; the only difference is that all
the well_formed() clauses have been removed.
Conveniently, there are no longer any requires clause at all, so it’s always possible
to call any of these functions.
This is also important if we want to prove the API “safe” in the Rust sense
(see this page).
The new client code
As before, the client code gets to reason about the TreeMap as if it were just a
Map.
Now, however, it’s a bit simpler because we don’t have to reason about tree_map.well_formed().
fn test() {
let mut tree_map = TreeMap::<bool>::new();
tree_map.insert(17, false);
tree_map.insert(18, false);
tree_map.insert(17, true);
assert(tree_map@ == map![17u64 => true, 18u64 => false]);
tree_map.delete(17);
assert(tree_map@ == map![18u64 => false]);
let elem17 = tree_map.get(17);
let elem18 = tree_map.get(18);
assert(elem17.is_none());
assert(elem18 == Some(&false));
test2(tree_map);
}
fn test2(tree_map: TreeMap<bool>) {
let mut tree_map = tree_map;
tree_map.insert(25, true);
tree_map.insert(100, true);
}Full source
The full source for this example can be found here.
Making it generic
In the previous sections, we devised a TreeMap<V> which a used fixed key type (u64).
In this section, we’ll show to make a TreeMap<K, V> which is generic over the key type K.
Defining a “total order”
The main reason this is challenging is that the BST requires a way of comparing
values of K, both for equality, and to obtain an ordering. This comparison is used both
in the implementation (to find the node for a given key, or to figure out where such
a node should be inserted) and in the well-formedness invariants that enforce
the BST ordering property.
We can define the concept of “total order” generically by creating a trait.
pub enum Cmp { Less, Equal, Greater }
pub trait TotalOrdered : Sized {
spec fn le(self, other: Self) -> bool;
proof fn reflexive(x: Self)
ensures Self::le(x, x);
proof fn transitive(x: Self, y: Self, z: Self)
requires Self::le(x, y), Self::le(y, z),
ensures Self::le(x, z);
proof fn antisymmetric(x: Self, y: Self)
requires Self::le(x, y), Self::le(y, x),
ensures x == y;
proof fn total(x: Self, y: Self)
ensures Self::le(x, y) || Self::le(y, x);
fn compare(&self, other: &Self) -> (c: Cmp)
ensures (match c {
Cmp::Less => self.le(*other) && self != other,
Cmp::Equal => self == other,
Cmp::Greater => other.le(*self) && self != other,
});
}This trait simultaneously:
- Requires a binary relation
leto exist - Requires it to satisfy the properties of a total order
- Requires an
executablethree-way comparison function to exist
There’s one simplification we’ve made here: we’re assuming that “equality” in the comparison
function is the same as spec equality.
This isn’t always suitable; some datatypes may have more than one way to represent the same
logical value. A more general specification would allow an ordering that respects
some arbitrary equivalence relation.
This is how vstd::hash_map::HashMapWithView works, for example.
To keep things simple for this demonstration though, we’ll use a total ordering that respects
spec equality.
Updating the struct and definitions
We’ll start by updating the structs to take a generic parameter K: TotalOrdered.
struct Node<K: TotalOrdered, V> {
key: K,
value: V,
left: Option<Box<Node<K, V>>>,
right: Option<Box<Node<K, V>>>,
}
pub struct TreeMap<K: TotalOrdered, V> {
root: Option<Box<Node<K, V>>>,
}We’ll also update the well-formedness condition to use the generic K::le instead of integer <=.
Where the original definition used a < b, we now use a.le(b) && a != b.
impl<K: TotalOrdered, V> Node<K, V> {
pub closed spec fn well_formed(self) -> bool
decreases self
{
&&& (forall |elem| #[trigger] Node::<K, V>::optional_as_map(self.left).dom().contains(elem) ==> elem.le(self.key) && elem != self.key)
&&& (forall |elem| #[trigger] Node::<K, V>::optional_as_map(self.right).dom().contains(elem) ==> self.key.le(elem) && elem != self.key)
&&& (match self.left {
Some(left_node) => left_node.well_formed(),
None => true,
})
&&& (match self.right {
Some(right_node) => right_node.well_formed(),
None => true,
})
}
}
impl<K: TotalOrdered, V> TreeMap<K, V> {
#[verifier::type_invariant]
spec fn well_formed(self) -> bool {
match self.root {
Some(node) => node.well_formed(),
None => true, // empty tree always well-formed
}
}
}Meanwhile, the definition of as_map doesn’t rely on the ordering function,
so it can be left alone, the same as before.
Updating the implementations and proofs
Updating the implementations take a bit more work, since we need more substantial proof code.
Whereas Verus has good automation for integer inequalities (<), it has no such automation
for our new, hand-made TotalOrdered trait. Thus, we need to add proof code to invoke
its properties manually.
Let’s take a look at Node::get.
The meat of the proof roughly goes as follows:
Supoose we’re looking for the key key which compares less than self.key.
Then we need to show that recursing into the left subtree gives the correct answer; for this,
it suffices to show that key is not in the right subtree.
Suppose (for contradiction) that key were in the right subtree.
Then (by the well-formedness invariant), we must have key > self.key.
But we already established that key < self.key. Contradiction.
(Formally, this contradiction can be obtained by invoking antisymmetry.)
impl<K: TotalOrdered, V> Node<K, V> {
fn get_from_optional(node: &Option<Box<Node<K, V>>>, key: K) -> Option<&V>
requires
node.is_some() ==> node.unwrap().well_formed(),
returns
(match node {
Some(node) => (if node.as_map().dom().contains(key) { Some(&node.as_map()[key]) } else { None }),
None => None,
}),
decreases node,
{
match node {
None => None,
Some(node) => {
node.get(key)
}
}
}
fn get(&self, key: K) -> Option<&V>
requires
self.well_formed(),
returns
(if self.as_map().dom().contains(key) { Some(&self.as_map()[key]) } else { None }),
decreases self,
{
match key.compare(&self.key) {
Cmp::Equal => {
Some(&self.value)
}
Cmp::Less => {
proof {
if Node::<K, V>::optional_as_map(self.right).dom().contains(key) {
TotalOrdered::antisymmetric(self.key, key);
assert(false);
}
assert(key != self.key);
assert((match self.left {
Some(node) => (if node.as_map().dom().contains(key) { Some(&node.as_map()[key]) } else { None }),
None => None,
}) == (if self.as_map().dom().contains(key) { Some(&self.as_map()[key]) } else { None }));
}
Self::get_from_optional(&self.left, key)
}
Cmp::Greater => {
proof {
if Node::<K, V>::optional_as_map(self.left).dom().contains(key) {
TotalOrdered::antisymmetric(self.key, key);
assert(false);
}
assert(key != self.key);
assert((match self.right {
Some(node) => (if node.as_map().dom().contains(key) { Some(&node.as_map()[key]) } else { None }),
None => None,
}) == (if self.as_map().dom().contains(key) { Some(&self.as_map()[key]) } else { None }));
}
Self::get_from_optional(&self.right, key)
}
}
}
}We can update insert and delete similarly, manually inserting lemma calls to invoke
the total-ordering properties where necessary.
Full source
The full source for this example can be found here.
Implementing Clone
As a finishing touch, let’s implement Clone for TreeMap<K, V>.
The main trick here will be in figuring out the correct specification for TreeMap::<K, V>::Clone.
Naturally, such an implementation will require both K: Clone and V: Clone.
However, to write a sensible clone implementation for the tree, we have to consider
what the implementations of K::clone and V::clone actually do.
Generally speaking, Verus imposes no constraints on the implementations of Clone,
so it is not necessarily true that a clone() call will return a value that is spec-equal
to its input.
With this in mind, to simplify this example,
we’re going to prove the following signature for TreeMap<K, V>::clone:
impl<K: Copy + TotalOrdered, V: Clone> Clone for TreeMap<K, V> {
fn clone(&self) -> (res: Self)
ensures self@.dom() =~= res@.dom(),
forall |key| #[trigger] res@.dom().contains(key) ==>
cloned::<V>(self@[key], res@[key]),
{
...
}
}We explain the details of this signature below.
Dealing with K::clone
In order to clone all the keys, we need K::clone to respect the ordering of elements;
otherwise during a clone operation,
we’d need to re-sort all the keys so that the resulting tree would be valid.
However, it’s unlikely that is desirable behavior. If K::clone doesn’t respect the
TotalOrdered implementation, it’s likely a user bug.
A general way to handle this would be to require that Clone actually be compatible
with the total-ordering in some sense.
However, you’ll
recall from the previous section that we’re already simplifying the “total ordered” specification
a bit. Likewise, we’re going to continue to keep things simple here by also requiring
that K: Copy.
As a result, we’ll be able to prove that our TreeMap clone implementation can preserve
all keys exactly, even when compared via spec equality. That is, we’ll be able to
ensure that self@.dom() =~= res@.dom().
Dealing with V::clone
So what about V? Again, we don’t know a priori what V::clone does. It might return
a value unequal to the imput; it might even be nondeterminstic. Therefore,
a cloned TreeMap may have different values than the original.
In order to specify TreeMap::<K, V>::clone as generically as possible, we choose
to write its ensures clause in terms of the ensures clause for V::clone.
This can be done using call_ensures.
The predicate call_ensures(V::clone, (&self@[key],), res@[key]) effectively says
“self@[key] and res@[key] are a possible input-output pair for V::clone”.
This predicate is a mouthful, so vstd provides a helper function:
cloned::<V>(self@[key], res@[key])
Understanding the implications of the signature
Let’s do a few examples.
First, consider cloning a TreeMap::<u64, u32>. The Verus standard library provides
a specification for u32::clone; it’s the same as a copy, i.e., a cloned u32 always
equals the input. As a result, we can deduce that cloning a TreeMap::<u64, u32> will
preserve its view exactly. We can prove this using extensional equality.
fn test_clone_u32(tree_map: TreeMap<u64, u32>) {
let tree_map2 = tree_map.clone();
assert(tree_map2@ =~= tree_map@);
}We can do the same for any type where clone guarantees spec-equality. Here’s another
example with a user-defined type.
struct IntWrapper {
pub int_value: u32,
}
impl Clone for IntWrapper {
fn clone(&self) -> (s: Self)
ensures s == *self
{
IntWrapper { int_value: self.int_value }
}
}
fn test_clone_int_wrapper(tree_map: TreeMap<u64, IntWrapper>) {
let tree_map2 = tree_map.clone();
assert(tree_map2@ =~= tree_map@);
}This works because of the postcondition on IntWrapper::clone, that is, ensures *s == self.
If you’re new to this style, it might seem initially surprising that
IntWrapper::clone has any effect on the verification of test_clone_int_wrapper, since
it doesn’t directly call IntWrapper::clone. In this case, the postcondition is referenced
indirectly via TreeMap<u64, IntWrapper>:clone.
Let’s do one more example, this time with a less precise clone function.
pub struct WeirdInt {
pub int_value: u32,
pub other: u32,
}
impl Clone for WeirdInt {
fn clone(&self) -> (s: Self)
ensures
s.int_value == self.int_value,
{
WeirdInt { int_value: self.int_value, other: 0 }
}
}
fn test_clone_weird_int(tree_map: TreeMap<u64, WeirdInt>) {
let tree_map2 = tree_map.clone();
// assert(tree_map2@ =~= tree_map@); // this would fail
assert(tree_map2@.dom() == tree_map@.dom());
assert(forall |k| tree_map@.dom().contains(k) ==>
tree_map2@[k].int_value == tree_map@[k].int_value);
}This example is a bit pathological; our struct, WeirdInt, has an extra field that doesn’t
get cloned. You could imagine real-life scenarios that have this property (for example,
if every struct needs to have a unique identifier). Anyway, the postcondition of
WeirdInt::clone doesn’t say both objects are equal, only that the int_value fields are equal.
This postcondition can then be inferred for each value in the map, as shown.
Implementing TreeMap::<K, V>::Clone.
As usual, we write the implementation as a recursive function.
It’s not necessary to implement Node::Clone; one could instead just implement a normal
recursive function as a helper for TreeMap::Clone; but it’s more Rust-idiomatic to do it
this way. This lets us call Option<Node<K, V>>::Clone
in the implementation of TreeMap::clone (the spec for Option::clone is provided by
vstd). However, you can see that there are a few ‘gotchas’ that need
to be worked around.
impl<K: Copy + TotalOrdered, V: Clone> Clone for Node<K, V> {
fn clone(&self) -> (res: Self)
ensures
self.well_formed() ==> res.well_formed(),
self.as_map().dom() =~= res.as_map().dom(),
forall |key| #[trigger] res.as_map().dom().contains(key) ==>
cloned::<V>(self.as_map()[key], res.as_map()[key]),
decreases self,
{
let res = Node {
key: self.key,
value: self.value.clone(),
// Ordinarily, we would use Option<Node>::clone rather than inlining
// the case statement here; we write it this way to work around
// this issue: https://github.com/verus-lang/verus/issues/1346
left: (match &self.left {
Some(node) => Some(Box::new((&**node).clone())),
None => None,
}),
right: (match &self.right {
Some(node) => Some(Box::new((&**node).clone())),
None => None,
}),
};
proof {
assert(Node::optional_as_map(res.left).dom() =~=
Node::optional_as_map(self.left).dom());
assert(Node::optional_as_map(res.right).dom() =~=
Node::optional_as_map(self.right).dom());
}
return res;
}
}
impl<K: Copy + TotalOrdered, V: Clone> Clone for TreeMap<K, V> {
fn clone(&self) -> (res: Self)
ensures self@.dom() =~= res@.dom(),
forall |key| #[trigger] res@.dom().contains(key) ==>
cloned::<V>(self@[key], res@[key]),
{
proof {
use_type_invariant(self);
}
TreeMap {
// This calls Option<Node<K, V>>::Clone
root: self.root.clone(),
}
}
}Full source
The full source for this example can be found here.
Full source for the examples
First draft
use vstd::prelude::*;
verus!{
struct Node<V> {
key: u64,
value: V,
left: Option<Box<Node<V>>>,
right: Option<Box<Node<V>>>,
}
pub struct TreeMap<V> {
root: Option<Box<Node<V>>>,
}
impl<V> Node<V> {
spec fn optional_as_map(node_opt: Option<Box<Node<V>>>) -> Map<u64, V>
decreases node_opt,
{
match node_opt {
None => Map::empty(),
Some(node) => node.as_map(),
}
}
spec fn as_map(self) -> Map<u64, V>
decreases self,
{
Node::<V>::optional_as_map(self.left)
.union_prefer_right(Node::<V>::optional_as_map(self.right))
.insert(self.key, self.value)
}
}
impl<V> TreeMap<V> {
pub closed spec fn as_map(self) -> Map<u64, V> {
Node::<V>::optional_as_map(self.root)
}
}
impl<V> View for TreeMap<V> {
type V = Map<u64, V>;
open spec fn view(&self) -> Map<u64, V> {
self.as_map()
}
}
impl<V> Node<V> {
spec fn well_formed(self) -> bool
decreases self,
{
&&& (forall |elem| Node::<V>::optional_as_map(self.left).dom().contains(elem) ==> elem < self.key)
&&& (forall |elem| Node::<V>::optional_as_map(self.right).dom().contains(elem) ==> elem > self.key)
&&& (match self.left {
Some(left_node) => left_node.well_formed(),
None => true,
})
&&& (match self.right {
Some(right_node) => right_node.well_formed(),
None => true,
})
}
}
impl<V> TreeMap<V> {
pub closed spec fn well_formed(self) -> bool {
match self.root {
Some(node) => node.well_formed(),
None => true, // empty tree always well-formed
}
}
}
impl<V> TreeMap<V> {
pub fn new() -> (tree_map: Self)
ensures
tree_map.well_formed(),
tree_map@ == Map::<u64, V>::empty(),
{
TreeMap::<V> { root: None }
}
}
impl<V> Node<V> {
fn insert_into_optional(node: &mut Option<Box<Node<V>>>, key: u64, value: V)
requires
old(node).is_some() ==> old(node).unwrap().well_formed(),
ensures
node.is_some() ==> node.unwrap().well_formed(),
Node::<V>::optional_as_map(*node) =~= Node::<V>::optional_as_map(*old(node)).insert(key, value),
decreases *old(node),
{
match node.take() {
None => {
*node = Some(Box::new(Node::<V> {
key: key,
value: value,
left: None,
right: None,
}));
}
Some(mut boxed_node) => {
(&mut *boxed_node).insert(key, value);
*node = Some(boxed_node);
}
}
}
fn insert(&mut self, key: u64, value: V)
requires
old(self).well_formed(),
ensures
self.well_formed(),
self.as_map() =~= old(self).as_map().insert(key, value),
decreases *old(self),
{
if key == self.key {
self.value = value;
assert(!Node::<V>::optional_as_map(self.left).dom().contains(key));
assert(!Node::<V>::optional_as_map(self.right).dom().contains(key));
} else if key < self.key {
Self::insert_into_optional(&mut self.left, key, value);
assert(!Node::<V>::optional_as_map(self.right).dom().contains(key));
} else {
Self::insert_into_optional(&mut self.right, key, value);
assert(!Node::<V>::optional_as_map(self.left).dom().contains(key));
}
}
}
impl<V> TreeMap<V> {
pub fn insert(&mut self, key: u64, value: V)
requires
old(self).well_formed(),
ensures
self.well_formed(),
self@ == old(self)@.insert(key, value),
{
Node::<V>::insert_into_optional(&mut self.root, key, value);
}
}
impl<V> Node<V> {
fn delete_from_optional(node: &mut Option<Box<Node<V>>>, key: u64)
requires
old(node).is_some() ==> old(node).unwrap().well_formed(),
ensures
node.is_some() ==> node.unwrap().well_formed(),
Node::<V>::optional_as_map(*node) =~= Node::<V>::optional_as_map(*old(node)).remove(key),
decreases *old(node),
{
if let Some(mut boxed_node) = node.take() {
if key == boxed_node.key {
assert(!Node::<V>::optional_as_map(boxed_node.left).dom().contains(key));
assert(!Node::<V>::optional_as_map(boxed_node.right).dom().contains(key));
if boxed_node.left.is_none() {
*node = boxed_node.right;
} else {
if boxed_node.right.is_none() {
*node = boxed_node.left;
} else {
let (popped_key, popped_value) = Node::<V>::delete_rightmost(&mut boxed_node.left);
boxed_node.key = popped_key;
boxed_node.value = popped_value;
*node = Some(boxed_node);
}
}
} else if key < boxed_node.key {
assert(!Node::<V>::optional_as_map(boxed_node.right).dom().contains(key));
Node::<V>::delete_from_optional(&mut boxed_node.left, key);
*node = Some(boxed_node);
} else {
assert(!Node::<V>::optional_as_map(boxed_node.left).dom().contains(key));
Node::<V>::delete_from_optional(&mut boxed_node.right, key);
*node = Some(boxed_node);
}
}
}
fn delete_rightmost(node: &mut Option<Box<Node<V>>>) -> (popped: (u64, V))
requires
old(node).is_some(),
old(node).unwrap().well_formed(),
ensures
node.is_some() ==> node.unwrap().well_formed(),
Node::<V>::optional_as_map(*node) =~= Node::<V>::optional_as_map(*old(node)).remove(popped.0),
Node::<V>::optional_as_map(*old(node)).dom().contains(popped.0),
Node::<V>::optional_as_map(*old(node))[popped.0] == popped.1,
forall |elem| Node::<V>::optional_as_map(*old(node)).dom().contains(elem) ==> popped.0 >= elem,
decreases *old(node),
{
let mut boxed_node = node.take().unwrap();
if boxed_node.right.is_none() {
*node = boxed_node.left;
assert(Node::<V>::optional_as_map(boxed_node.right) =~= Map::empty());
assert(!Node::<V>::optional_as_map(boxed_node.left).dom().contains(boxed_node.key));
return (boxed_node.key, boxed_node.value);
} else {
let (popped_key, popped_value) = Node::<V>::delete_rightmost(&mut boxed_node.right);
assert(!Node::<V>::optional_as_map(boxed_node.left).dom().contains(popped_key));
*node = Some(boxed_node);
return (popped_key, popped_value);
}
}
}
impl<V> TreeMap<V> {
pub fn delete(&mut self, key: u64)
requires
old(self).well_formed(),
ensures
self.well_formed(),
self@ == old(self)@.remove(key),
{
Node::<V>::delete_from_optional(&mut self.root, key);
}
}
impl<V> Node<V> {
fn get_from_optional(node: &Option<Box<Node<V>>>, key: u64) -> Option<&V>
requires
node.is_some() ==> node.unwrap().well_formed(),
returns
(match node {
Some(node) => (if node.as_map().dom().contains(key) { Some(&node.as_map()[key]) } else { None }),
None => None,
}),
decreases node,
{
match node {
None => None,
Some(node) => {
node.get(key)
}
}
}
fn get(&self, key: u64) -> Option<&V>
requires
self.well_formed(),
returns
(if self.as_map().dom().contains(key) { Some(&self.as_map()[key]) } else { None }),
decreases self,
{
if key == self.key {
Some(&self.value)
} else if key < self.key {
proof { assert(!Node::<V>::optional_as_map(self.right).dom().contains(key)); }
Self::get_from_optional(&self.left, key)
} else {
proof { assert(!Node::<V>::optional_as_map(self.left).dom().contains(key)); }
Self::get_from_optional(&self.right, key)
}
}
}
impl<V> TreeMap<V> {
pub fn get(&self, key: u64) -> Option<&V>
requires
self.well_formed(),
returns
(if self@.dom().contains(key) { Some(&self@[key]) } else { None }),
{
Node::<V>::get_from_optional(&self.root, key)
}
}
fn test() {
let mut tree_map = TreeMap::<bool>::new();
tree_map.insert(17, false);
tree_map.insert(18, false);
tree_map.insert(17, true);
assert(tree_map@ == map![17u64 => true, 18u64 => false]);
tree_map.delete(17);
assert(tree_map@ == map![18u64 => false]);
let elem17 = tree_map.get(17);
let elem18 = tree_map.get(18);
assert(elem17.is_none());
assert(elem18 == Some(&false));
}
fn test2() {
let mut tree_map = TreeMap::<bool>::new();
test_callee(tree_map);
}
fn test_callee(tree_map: TreeMap<bool>)
requires
tree_map.well_formed(),
{
let mut tree_map = tree_map;
tree_map.insert(25, true);
tree_map.insert(100, true);
}
}Version with type invariants
use vstd::prelude::*;
verus!{
struct Node<V> {
key: u64,
value: V,
left: Option<Box<Node<V>>>,
right: Option<Box<Node<V>>>,
}
pub struct TreeMap<V> {
root: Option<Box<Node<V>>>,
}
impl<V> Node<V> {
spec fn optional_as_map(node_opt: Option<Box<Node<V>>>) -> Map<u64, V>
decreases node_opt,
{
match node_opt {
None => Map::empty(),
Some(node) => node.as_map(),
}
}
spec fn as_map(self) -> Map<u64, V>
decreases self,
{
Node::<V>::optional_as_map(self.left)
.union_prefer_right(Node::<V>::optional_as_map(self.right))
.insert(self.key, self.value)
}
}
impl<V> TreeMap<V> {
pub closed spec fn as_map(self) -> Map<u64, V> {
Node::<V>::optional_as_map(self.root)
}
}
impl<V> View for TreeMap<V> {
type V = Map<u64, V>;
open spec fn view(&self) -> Map<u64, V> {
self.as_map()
}
}
impl<V> Node<V> {
spec fn well_formed(self) -> bool
decreases self
{
&&& (forall |elem| Node::<V>::optional_as_map(self.left).dom().contains(elem) ==> elem < self.key)
&&& (forall |elem| Node::<V>::optional_as_map(self.right).dom().contains(elem) ==> elem > self.key)
&&& (match self.left {
Some(left_node) => left_node.well_formed(),
None => true,
})
&&& (match self.right {
Some(right_node) => right_node.well_formed(),
None => true,
})
}
}
impl<V> TreeMap<V> {
#[verifier::type_invariant]
spec fn well_formed(self) -> bool {
match self.root {
Some(node) => node.well_formed(),
None => true, // empty tree always well-formed
}
}
}
impl<V> TreeMap<V> {
pub fn new() -> (s: Self)
ensures
s@ == Map::<u64, V>::empty()
{
TreeMap::<V> { root: None }
}
}
impl<V> Node<V> {
fn insert_into_optional(node: &mut Option<Box<Node<V>>>, key: u64, value: V)
requires
old(node).is_some() ==> old(node).unwrap().well_formed(),
ensures
node.is_some() ==> node.unwrap().well_formed(),
Node::<V>::optional_as_map(*node) =~= Node::<V>::optional_as_map(*old(node)).insert(key, value),
decreases *old(node),
{
if node.is_none() {
*node = Some(Box::new(Node::<V> {
key: key,
value: value,
left: None,
right: None,
}));
} else {
let mut tmp = None;
std::mem::swap(&mut tmp, node);
let mut boxed_node = tmp.unwrap();
(&mut *boxed_node).insert(key, value);
*node = Some(boxed_node);
}
}
fn insert(&mut self, key: u64, value: V)
requires
old(self).well_formed(),
ensures
self.well_formed(),
self.as_map() =~= old(self).as_map().insert(key, value),
decreases *old(self),
{
if key == self.key {
self.value = value;
assert(!Node::<V>::optional_as_map(self.left).dom().contains(key));
assert(!Node::<V>::optional_as_map(self.right).dom().contains(key));
} else if key < self.key {
Self::insert_into_optional(&mut self.left, key, value);
assert(!Node::<V>::optional_as_map(self.right).dom().contains(key));
} else {
Self::insert_into_optional(&mut self.right, key, value);
assert(!Node::<V>::optional_as_map(self.left).dom().contains(key));
}
}
}
impl<V> TreeMap<V> {
pub fn insert(&mut self, key: u64, value: V)
ensures
self@ == old(self)@.insert(key, value),
{
proof { use_type_invariant(&*self); }
let mut root = None;
std::mem::swap(&mut root, &mut self.root);
Node::<V>::insert_into_optional(&mut root, key, value);
self.root = root;
}
}
impl<V> Node<V> {
fn delete_from_optional(node: &mut Option<Box<Node<V>>>, key: u64)
requires
old(node).is_some() ==> old(node).unwrap().well_formed(),
ensures
node.is_some() ==> node.unwrap().well_formed(),
Node::<V>::optional_as_map(*node) =~= Node::<V>::optional_as_map(*old(node)).remove(key),
decreases *old(node),
{
if node.is_some() {
let mut tmp = None;
std::mem::swap(&mut tmp, node);
let mut boxed_node = tmp.unwrap();
if key == boxed_node.key {
assert(!Node::<V>::optional_as_map(boxed_node.left).dom().contains(key));
assert(!Node::<V>::optional_as_map(boxed_node.right).dom().contains(key));
if boxed_node.left.is_none() {
*node = boxed_node.right;
} else {
if boxed_node.right.is_none() {
*node = boxed_node.left;
} else {
let (popped_key, popped_value) = Node::<V>::delete_rightmost(&mut boxed_node.left);
boxed_node.key = popped_key;
boxed_node.value = popped_value;
*node = Some(boxed_node);
}
}
} else if key < boxed_node.key {
assert(!Node::<V>::optional_as_map(boxed_node.right).dom().contains(key));
Node::<V>::delete_from_optional(&mut boxed_node.left, key);
*node = Some(boxed_node);
} else {
assert(!Node::<V>::optional_as_map(boxed_node.left).dom().contains(key));
Node::<V>::delete_from_optional(&mut boxed_node.right, key);
*node = Some(boxed_node);
}
}
}
fn delete_rightmost(node: &mut Option<Box<Node<V>>>) -> (popped: (u64, V))
requires
old(node).is_some(),
old(node).unwrap().well_formed(),
ensures
node.is_some() ==> node.unwrap().well_formed(),
Node::<V>::optional_as_map(*node) =~= Node::<V>::optional_as_map(*old(node)).remove(popped.0),
Node::<V>::optional_as_map(*old(node)).dom().contains(popped.0),
Node::<V>::optional_as_map(*old(node))[popped.0] == popped.1,
forall |elem| Node::<V>::optional_as_map(*old(node)).dom().contains(elem) ==> popped.0 >= elem,
decreases *old(node),
{
let mut tmp = None;
std::mem::swap(&mut tmp, node);
let mut boxed_node = tmp.unwrap();
if boxed_node.right.is_none() {
*node = boxed_node.left;
assert(Node::<V>::optional_as_map(boxed_node.right) =~= Map::empty());
assert(!Node::<V>::optional_as_map(boxed_node.left).dom().contains(boxed_node.key));
return (boxed_node.key, boxed_node.value);
} else {
let (popped_key, popped_value) = Node::<V>::delete_rightmost(&mut boxed_node.right);
assert(!Node::<V>::optional_as_map(boxed_node.left).dom().contains(popped_key));
*node = Some(boxed_node);
return (popped_key, popped_value);
}
}
}
impl<V> TreeMap<V> {
pub fn delete(&mut self, key: u64)
ensures
self@ == old(self)@.remove(key),
{
proof { use_type_invariant(&*self); }
let mut root = None;
std::mem::swap(&mut root, &mut self.root);
Node::<V>::delete_from_optional(&mut root, key);
self.root = root;
}
}
impl<V> Node<V> {
fn get_from_optional(node: &Option<Box<Node<V>>>, key: u64) -> Option<&V>
requires
node.is_some() ==> node.unwrap().well_formed(),
returns
(match node {
Some(node) => (if node.as_map().dom().contains(key) { Some(&node.as_map()[key]) } else { None }),
None => None,
}),
decreases node,
{
match node {
None => None,
Some(node) => {
node.get(key)
}
}
}
fn get(&self, key: u64) -> Option<&V>
requires
self.well_formed(),
returns
(if self.as_map().dom().contains(key) { Some(&self.as_map()[key]) } else { None }),
decreases self,
{
if key == self.key {
Some(&self.value)
} else if key < self.key {
proof { assert(!Node::<V>::optional_as_map(self.right).dom().contains(key)); }
Self::get_from_optional(&self.left, key)
} else {
proof { assert(!Node::<V>::optional_as_map(self.left).dom().contains(key)); }
Self::get_from_optional(&self.right, key)
}
}
}
impl<V> TreeMap<V> {
pub fn get(&self, key: u64) -> Option<&V>
returns
(if self@.dom().contains(key) { Some(&self@[key]) } else { None }),
{
proof { use_type_invariant(&*self); }
Node::<V>::get_from_optional(&self.root, key)
}
}
fn test() {
let mut tree_map = TreeMap::<bool>::new();
tree_map.insert(17, false);
tree_map.insert(18, false);
tree_map.insert(17, true);
assert(tree_map@ == map![17u64 => true, 18u64 => false]);
tree_map.delete(17);
assert(tree_map@ == map![18u64 => false]);
let elem17 = tree_map.get(17);
let elem18 = tree_map.get(18);
assert(elem17.is_none());
assert(elem18 == Some(&false));
test2(tree_map);
}
fn test2(tree_map: TreeMap<bool>) {
let mut tree_map = tree_map;
tree_map.insert(25, true);
tree_map.insert(100, true);
}
}Version with generic key type and Clone implementation
use vstd::prelude::*;
verus!{
pub enum Cmp { Less, Equal, Greater }
pub trait TotalOrdered : Sized {
spec fn le(self, other: Self) -> bool;
proof fn reflexive(x: Self)
ensures Self::le(x, x);
proof fn transitive(x: Self, y: Self, z: Self)
requires Self::le(x, y), Self::le(y, z),
ensures Self::le(x, z);
proof fn antisymmetric(x: Self, y: Self)
requires Self::le(x, y), Self::le(y, x),
ensures x == y;
proof fn total(x: Self, y: Self)
ensures Self::le(x, y) || Self::le(y, x);
fn compare(&self, other: &Self) -> (c: Cmp)
ensures (match c {
Cmp::Less => self.le(*other) && self != other,
Cmp::Equal => self == other,
Cmp::Greater => other.le(*self) && self != other,
});
}
struct Node<K: TotalOrdered, V> {
key: K,
value: V,
left: Option<Box<Node<K, V>>>,
right: Option<Box<Node<K, V>>>,
}
pub struct TreeMap<K: TotalOrdered, V> {
root: Option<Box<Node<K, V>>>,
}
impl<K: TotalOrdered, V> Node<K, V> {
spec fn optional_as_map(node_opt: Option<Box<Node<K, V>>>) -> Map<K, V>
decreases node_opt,
{
match node_opt {
None => Map::empty(),
Some(node) => node.as_map(),
}
}
pub closed spec fn as_map(self) -> Map<K, V>
decreases self,
{
Node::<K, V>::optional_as_map(self.left)
.union_prefer_right(Node::<K, V>::optional_as_map(self.right))
.insert(self.key, self.value)
}
}
impl<K: TotalOrdered, V> TreeMap<K, V> {
pub closed spec fn as_map(self) -> Map<K, V> {
Node::<K, V>::optional_as_map(self.root)
}
}
impl<K: TotalOrdered, V> View for TreeMap<K, V> {
type V = Map<K, V>;
open spec fn view(&self) -> Map<K, V> {
self.as_map()
}
}
impl<K: TotalOrdered, V> Node<K, V> {
pub closed spec fn well_formed(self) -> bool
decreases self
{
&&& (forall |elem| #[trigger] Node::<K, V>::optional_as_map(self.left).dom().contains(elem) ==> elem.le(self.key) && elem != self.key)
&&& (forall |elem| #[trigger] Node::<K, V>::optional_as_map(self.right).dom().contains(elem) ==> self.key.le(elem) && elem != self.key)
&&& (match self.left {
Some(left_node) => left_node.well_formed(),
None => true,
})
&&& (match self.right {
Some(right_node) => right_node.well_formed(),
None => true,
})
}
}
impl<K: TotalOrdered, V> TreeMap<K, V> {
#[verifier::type_invariant]
spec fn well_formed(self) -> bool {
match self.root {
Some(node) => node.well_formed(),
None => true, // empty tree always well-formed
}
}
}
impl<K: TotalOrdered, V> TreeMap<K, V> {
pub fn new() -> (s: Self)
ensures
s@ == Map::<K, V>::empty(),
{
TreeMap::<K, V> { root: None }
}
}
impl<K: TotalOrdered, V> Node<K, V> {
fn insert_into_optional(node: &mut Option<Box<Node<K, V>>>, key: K, value: V)
requires
old(node).is_some() ==> old(node).unwrap().well_formed(),
ensures
node.is_some() ==> node.unwrap().well_formed(),
Node::<K, V>::optional_as_map(*node) =~= Node::<K, V>::optional_as_map(*old(node)).insert(key, value),
decreases *old(node),
{
if node.is_none() {
*node = Some(Box::new(Node::<K, V> {
key: key,
value: value,
left: None,
right: None,
}));
} else {
let mut tmp = None;
std::mem::swap(&mut tmp, node);
let mut boxed_node = tmp.unwrap();
(&mut *boxed_node).insert(key, value);
*node = Some(boxed_node);
}
}
fn insert(&mut self, key: K, value: V)
requires
old(self).well_formed(),
ensures
self.well_formed(),
self.as_map() =~= old(self).as_map().insert(key, value),
decreases *old(self),
{
match key.compare(&self.key) {
Cmp::Equal => {
self.value = value;
assert(!Node::<K, V>::optional_as_map(self.left).dom().contains(key));
assert(!Node::<K, V>::optional_as_map(self.right).dom().contains(key));
}
Cmp::Less => {
Self::insert_into_optional(&mut self.left, key, value);
proof {
if self.key.le(key) {
TotalOrdered::antisymmetric(self.key, key);
}
assert(!Node::<K, V>::optional_as_map(self.right).dom().contains(key));
}
}
Cmp::Greater => {
Self::insert_into_optional(&mut self.right, key, value);
proof {
if key.le(self.key) {
TotalOrdered::antisymmetric(self.key, key);
}
assert(!Node::<K, V>::optional_as_map(self.left).dom().contains(key));
}
}
}
}
}
impl<K: TotalOrdered, V> TreeMap<K, V> {
pub fn insert(&mut self, key: K, value: V)
ensures
self@ == old(self)@.insert(key, value)
{
proof { use_type_invariant(&*self); }
let mut root = None;
std::mem::swap(&mut root, &mut self.root);
Node::<K, V>::insert_into_optional(&mut root, key, value);
self.root = root;
}
}
impl<K: TotalOrdered, V> Node<K, V> {
fn delete_from_optional(node: &mut Option<Box<Node<K, V>>>, key: K)
requires
old(node).is_some() ==> old(node).unwrap().well_formed(),
ensures
node.is_some() ==> node.unwrap().well_formed(),
Node::<K, V>::optional_as_map(*node) =~= Node::<K, V>::optional_as_map(*old(node)).remove(key),
decreases *old(node),
{
if node.is_some() {
let mut tmp = None;
std::mem::swap(&mut tmp, node);
let mut boxed_node = tmp.unwrap();
match key.compare(&boxed_node.key) {
Cmp::Equal => {
assert(!Node::<K, V>::optional_as_map(boxed_node.left).dom().contains(key));
assert(!Node::<K, V>::optional_as_map(boxed_node.right).dom().contains(key));
assert(boxed_node.right.is_some() ==> boxed_node.right.unwrap().well_formed());
assert(boxed_node.left.is_some() ==> boxed_node.left.unwrap().well_formed());
if boxed_node.left.is_none() {
*node = boxed_node.right;
} else {
if boxed_node.right.is_none() {
*node = boxed_node.left;
} else {
let (popped_key, popped_value) = Node::<K, V>::delete_rightmost(&mut boxed_node.left);
boxed_node.key = popped_key;
boxed_node.value = popped_value;
*node = Some(boxed_node);
proof {
assert forall |elem| #[trigger] Node::<K, V>::optional_as_map(node.unwrap().right).dom().contains(elem) implies node.unwrap().key.le(elem) && elem != node.unwrap().key
by {
TotalOrdered::transitive(node.unwrap().key, key, elem);
if elem == node.unwrap().key {
TotalOrdered::antisymmetric(elem, key);
}
}
}
}
}
}
Cmp::Less => {
proof {
if Node::<K, V>::optional_as_map(boxed_node.right).dom().contains(key) {
TotalOrdered::antisymmetric(boxed_node.key, key);
assert(false);
}
}
Node::<K, V>::delete_from_optional(&mut boxed_node.left, key);
*node = Some(boxed_node);
}
Cmp::Greater => {
proof {
if Node::<K, V>::optional_as_map(boxed_node.left).dom().contains(key) {
TotalOrdered::antisymmetric(boxed_node.key, key);
assert(false);
}
}
Node::<K, V>::delete_from_optional(&mut boxed_node.right, key);
*node = Some(boxed_node);
}
}
}
}
fn delete_rightmost(node: &mut Option<Box<Node<K, V>>>) -> (popped: (K, V))
requires
old(node).is_some(),
old(node).unwrap().well_formed(),
ensures
node.is_some() ==> node.unwrap().well_formed(),
Node::<K, V>::optional_as_map(*node) =~= Node::<K, V>::optional_as_map(*old(node)).remove(popped.0),
Node::<K, V>::optional_as_map(*old(node)).dom().contains(popped.0),
Node::<K, V>::optional_as_map(*old(node))[popped.0] == popped.1,
forall |elem| #[trigger] Node::<K, V>::optional_as_map(*old(node)).dom().contains(elem) ==> elem.le(popped.0),
decreases *old(node),
{
let mut tmp = None;
std::mem::swap(&mut tmp, node);
let mut boxed_node = tmp.unwrap();
if boxed_node.right.is_none() {
*node = boxed_node.left;
proof {
assert(Node::<K, V>::optional_as_map(boxed_node.right) =~= Map::empty());
assert(!Node::<K, V>::optional_as_map(boxed_node.left).dom().contains(boxed_node.key));
TotalOrdered::reflexive(boxed_node.key);
}
return (boxed_node.key, boxed_node.value);
} else {
let (popped_key, popped_value) = Node::<K, V>::delete_rightmost(&mut boxed_node.right);
proof {
if Node::<K, V>::optional_as_map(boxed_node.left).dom().contains(popped_key) {
TotalOrdered::antisymmetric(boxed_node.key, popped_key);
assert(false);
}
assert forall |elem| #[trigger] Node::<K, V>::optional_as_map(*old(node)).dom().contains(elem) implies elem.le(popped_key)
by {
if elem.le(boxed_node.key) {
TotalOrdered::transitive(elem, boxed_node.key, popped_key);
}
}
}
*node = Some(boxed_node);
return (popped_key, popped_value);
}
}
}
impl<K: TotalOrdered, V> TreeMap<K, V> {
pub fn delete(&mut self, key: K)
ensures
self@ == old(self)@.remove(key),
{
proof { use_type_invariant(&*self); }
let mut root = None;
std::mem::swap(&mut root, &mut self.root);
Node::<K, V>::delete_from_optional(&mut root, key);
self.root = root;
}
}
impl<K: TotalOrdered, V> Node<K, V> {
fn get_from_optional(node: &Option<Box<Node<K, V>>>, key: K) -> Option<&V>
requires
node.is_some() ==> node.unwrap().well_formed(),
returns
(match node {
Some(node) => (if node.as_map().dom().contains(key) { Some(&node.as_map()[key]) } else { None }),
None => None,
}),
decreases node,
{
match node {
None => None,
Some(node) => {
node.get(key)
}
}
}
fn get(&self, key: K) -> Option<&V>
requires
self.well_formed(),
returns
(if self.as_map().dom().contains(key) { Some(&self.as_map()[key]) } else { None }),
decreases self,
{
match key.compare(&self.key) {
Cmp::Equal => {
Some(&self.value)
}
Cmp::Less => {
proof {
if Node::<K, V>::optional_as_map(self.right).dom().contains(key) {
TotalOrdered::antisymmetric(self.key, key);
assert(false);
}
assert(key != self.key);
assert((match self.left {
Some(node) => (if node.as_map().dom().contains(key) { Some(&node.as_map()[key]) } else { None }),
None => None,
}) == (if self.as_map().dom().contains(key) { Some(&self.as_map()[key]) } else { None }));
}
Self::get_from_optional(&self.left, key)
}
Cmp::Greater => {
proof {
if Node::<K, V>::optional_as_map(self.left).dom().contains(key) {
TotalOrdered::antisymmetric(self.key, key);
assert(false);
}
assert(key != self.key);
assert((match self.right {
Some(node) => (if node.as_map().dom().contains(key) { Some(&node.as_map()[key]) } else { None }),
None => None,
}) == (if self.as_map().dom().contains(key) { Some(&self.as_map()[key]) } else { None }));
}
Self::get_from_optional(&self.right, key)
}
}
}
}
impl<K: TotalOrdered, V> TreeMap<K, V> {
pub fn get(&self, key: K) -> Option<&V>
returns
(if self@.dom().contains(key) { Some(&self@[key]) } else { None }),
{
proof { use_type_invariant(&*self); }
Node::<K, V>::get_from_optional(&self.root, key)
}
}
impl<K: Copy + TotalOrdered, V: Clone> Clone for Node<K, V> {
fn clone(&self) -> (res: Self)
ensures
self.well_formed() ==> res.well_formed(),
self.as_map().dom() =~= res.as_map().dom(),
forall |key| #[trigger] res.as_map().dom().contains(key) ==>
cloned::<V>(self.as_map()[key], res.as_map()[key]),
decreases self,
{
let res = Node {
key: self.key,
value: self.value.clone(),
// Ordinarily, we would use Option<Node>::clone rather than inlining
// the case statement here; we write it this way to work around
// this issue: https://github.com/verus-lang/verus/issues/1346
left: (match &self.left {
Some(node) => Some(Box::new((&**node).clone())),
None => None,
}),
right: (match &self.right {
Some(node) => Some(Box::new((&**node).clone())),
None => None,
}),
};
proof {
assert(Node::optional_as_map(res.left).dom() =~=
Node::optional_as_map(self.left).dom());
assert(Node::optional_as_map(res.right).dom() =~=
Node::optional_as_map(self.right).dom());
}
return res;
}
}
impl<K: Copy + TotalOrdered, V: Clone> Clone for TreeMap<K, V> {
fn clone(&self) -> (res: Self)
ensures self@.dom() =~= res@.dom(),
forall |key| #[trigger] res@.dom().contains(key) ==>
cloned::<V>(self@[key], res@[key]),
{
proof {
use_type_invariant(self);
}
TreeMap {
// This calls Option<Node<K, V>>::Clone
root: self.root.clone(),
}
}
}
impl TotalOrdered for u64 {
open spec fn le(self, other: Self) -> bool { self <= other }
proof fn reflexive(x: Self) { }
proof fn transitive(x: Self, y: Self, z: Self) { }
proof fn antisymmetric(x: Self, y: Self) { }
proof fn total(x: Self, y: Self) { }
fn compare(&self, other: &Self) -> (c: Cmp) {
if *self == *other {
Cmp::Equal
} else if *self < *other {
Cmp::Less
} else {
Cmp::Greater
}
}
}
fn test() {
let mut tree_map = TreeMap::<u64, bool>::new();
tree_map.insert(17, false);
tree_map.insert(18, false);
tree_map.insert(17, true);
assert(tree_map@ == map![17u64 => true, 18u64 => false]);
tree_map.delete(17);
assert(tree_map@ == map![18u64 => false]);
let elem17 = tree_map.get(17);
let elem18 = tree_map.get(18);
assert(elem17.is_none());
assert(elem18 == Some(&false));
test2(tree_map);
}
fn test2(tree_map: TreeMap<u64, bool>) {
let mut tree_map = tree_map;
tree_map.insert(25, true);
tree_map.insert(100, true);
}
fn test_clone_u32(tree_map: TreeMap<u64, u32>) {
let tree_map2 = tree_map.clone();
assert(tree_map2@ =~= tree_map@);
}
struct IntWrapper {
pub int_value: u32,
}
impl Clone for IntWrapper {
fn clone(&self) -> (s: Self)
ensures s == *self
{
IntWrapper { int_value: self.int_value }
}
}
fn test_clone_int_wrapper(tree_map: TreeMap<u64, IntWrapper>) {
let tree_map2 = tree_map.clone();
assert(tree_map2@ =~= tree_map@);
}
pub struct WeirdInt {
pub int_value: u32,
pub other: u32,
}
impl Clone for WeirdInt {
fn clone(&self) -> (s: Self)
ensures
s.int_value == self.int_value,
{
WeirdInt { int_value: self.int_value, other: 0 }
}
}
fn test_clone_weird_int(tree_map: TreeMap<u64, WeirdInt>) {
let tree_map2 = tree_map.clone();
// assert(tree_map2@ =~= tree_map@); // this would fail
assert(tree_map2@.dom() == tree_map@.dom());
assert(forall |k| tree_map@.dom().contains(k) ==>
tree_map2@[k].int_value == tree_map@[k].int_value);
}
}Interacting with unverified code
We typically only verify a portion of a Rust code base. This chapter discusses how to call unverified code from verified code, as well as some caveats and strategies for safely allowing unverified code to call verified code
Calling unverified code from verified code
Often we only verify part of a system, which means that we need verified code to call unverified code. To do this, we need to make Verus aware of the unverified code, and we need to tell Verus what it should assume without proof.
Specifications without proof
One way to apply an assumption to an unverified function is to use the #[verifier::external_body] attribute.
This tells Verus to process the specification of a function, without verifying or processing its body.
Thus, it causes Verus to assume the specification without proof. Obviously, this should be used with care,
with wrong specifications can subvert Verus’s guarantees!
#[verifier::external_body]
fn fib_impl(n: u64) -> (result: u64)
requires
fib(n as nat) <= u64::MAX
ensures
result == fib(n as nat),
{
if n == 0 {
return 0;
}
let mut prev: u64 = 0;
let mut cur: u64 = 1;
let mut i: u64 = 1;
while i < n {
i = i + 1;
let new_cur = cur + prev;
prev = cur;
cur = new_cur;
}
cur
}This implementation is correct, but unproved. If the external_body attribute were removed,
Verus would attempt to verify the body and fail because of the lack of loop invariants.
(See here for more about this particular example.)
Applying specifications to existing library functions
It’s common that you want to apply a specification to an existing function, e.g., one defined in some library crate, or even in the Rust standard library.
One way to do this is to write a “wrapper function” with external_body which calls the
library function. For example, let’s suppose we want to call std::mem::swap. We could write this wrapper function:
#[verifier::external_body]
fn wrapper_swap<T>(a: &mut T, b: &mut T)
ensures
*a == *old(b),
*b == *old(a),
{
std::mem::swap(a, b);
}However, this may be incovenient, because now you need to call wrapper_swap instead of
the more familiar std::mem::swap. If you want to apply the specification to
std::mem::swap itself, so that you can call it from verified code, you can
use the assume_specification directive, which goes at the item level (like functions).
pub assume_specification<T>[ std::mem::swap::<T> ](a: &mut T, b: &mut T)
ensures
*a == *old(b),
*b == *old(a);Now you can call std::mem::swap from verified code.
(Note though, that vstd already provides this specification for std::mem::swap. Verus doesn’t allow duplicate specifications,
so it won’t let you declare a second one. If you want to try out this example yourself, you’ll need to run Verus with the --no-vstd flag, but this is not recommended for general usage.)
Standard library specifications
In fact, vstd provides a wide range of specifications for the standard library using this directive, so as long as you run Verus while importing vstd (as in normal usage), you will automatically import these specifications, as documented here.
Of course, if vstd doesn’t provide a specification for a stdlib function you’d like to use,
you can also add an assume_specification to your own crate.
Making Verus aware of types
Sometimes, Verus will complain that it doesn’t recognize a type; for this, you just need
to make Verus aware of it. For this, you can use the #[verifier::external_type_specification] attribute.
This will make Verus aware of the SomeStruct:
#[verifier::external_type_specification]
struct ExSomeStruct(SomeStruct);It should have exactly this form, with the parentheses and semicolon. The ExSomeStruct name can be arbitrary; this is just an artificial type used for the directive and shouldn’t be referenced
anywhere else.
This declaration makes Verus aware of the type SomeStruct and all its fields (and for an enum, all its variants). If you don’t want Verus to be aware of the fields/variants, you can also mark it #[verifier::external_body].
Adding specifications for external traits
You can also add specifications to external traits using the #[verifier::external_trait_specification] attribute. This lets you add requires and ensures clauses to trait methods, and optionally define spec helper functions with #[verifier::external_trait_extension].
For details and examples, see External trait specifications.
Calling verified code from unverified code
When writing verified code that may be called from unverified code, you should be careful with the specifications you provide on your external API. In particular, any preconditions on external API functions are assumptions about what your caller will pass in. The stronger the precondition (i.e., assumption), the more likely it is that a caller will fail to meet it, meaning that all of your verification work may be undermined.
Ideally, you should aim to have no preconditions on your external API;
if you don’t make any assumptions about your caller, you’ll never be disappointed!
You can check if your verified crate meets these requirements by using the flag -V check-safe-api.
Specifically, this flag will check if your crate is unconditionally safe to be used from
any unverified code that does not use unsafe.
Tips for eliminating preconditions
If your API does have important preconditions, you might consider adding
a wrapper around it that has no preconditions, dynamically checks that the
necessary preconditions hold, and then calls an internal version of your API.
Verus will, of course, check that your dynamic checks suffice to establish the necessary
preconditions. You can then mark the inner function—the one with the preconditions—as unsafe.
This will prevent the client from calling it without declaring its intent to bypass the checks.
For example:
pub unsafe fn index_unchecked<T>(vec: &Vec<T>, i: usize) -> &T
requires i < vec.len()
{
/* ... */
}
pub fn index<T>(vec: &Vec<T>, i: usize) -> Option<&T>
{
if i < vec.len() {
Some(index_unchecked(vec, i))
} else {
None
}
}If your API involves passing state back and forth between your code and your caller, then you can consider defining a public struct with private fields that contain your state. Since your caller cannot create their own versions of the struct, or modify values in the structs you give them, then you can (reasonably) safely use pre- and post-conditions on your API (or type invariants to maintain invariants about the contents of such structs.
Understanding the guarantees of a verified program
A persistent challenge with verified software is understanding what, exactly, is being verified and what guarantees are being given. Verified code doesn’t run in a vacuum; verified code ofter interacts with unverified code, possibly in either direction. This chapter documents technical information need to properly understand how verified code might interact with unverified code.
Assumptions and trusted components
Often times, it’s not possible to verify every line of code and some things need to be assumed. In such cases, the ultimate correctness of the code is dependent not just on verification but on the assumptions being made.
Assumptions can be introduced through the following mechanisms:
- As
assumestatement - An axiom - any proof function introduced with
#[verifier::external_body] - An axiomatic specification - any exec function introduced with
#[verifier::external_body]or#[verifier::external_fn_specification] #[verifier::external](See below.)
Types (structs and enums) can also be marked as #[verifier::external_body],
though to be pedantic, this does not introduce a new assumption per se.
In practice, though, such types are usually associated with additional assumptions
to make them useful.
The #[verifier::external] attribute
The #[verifier::external] annotation tells Verus to ignore an item entirely.
It can be applied to any item - a function, trait, trait implementation, type, etc.
For many items (functions, types, trait declarations), this does not, on its own,
introduce any new “assumptions” about that item.
Attempting to call an external function from a verified
function, for example, will result in an error from Verus. In practice, a developer
will often call an external function (say f) from an external_body function (say g),
in which case, the external_body attribute introduces assumptions about g, thus
indirectly introducing assumptions about f.
Furthermore, adding #[verifier::external] to a trait implementation requires even more
careful consideration, as Verus relies on rustc’s trait-checking for some things,
so trait implementations can sometimes affect what code gets accepted or rejected.
For example:
#[verifier::external]
unsafe impl Send for X { }Memory safety is conditional on verification
Let’s briefly compare and contrast the philosophies of Rust and Verus with regards to memory safety. Memory safety, here, refers to a program being free of any undefined behavior (UB) in its memory access. Both Rust and Verus rely on memory safety being upheld; in turn, they both do a great deal to enforce it. However, they enforce it in different ways.
Rust’s enforcement of memory safety is built around a contract between “safe” and
“unsafe” code. The first chapter of the Rustonomicon
summarizes the philosophy. In short: any “safe” code (i.e., code free of the unsafe keyword)
must be memory safe, enforced by Rust itself via its type-checker and borrow-checker,
regardless of user error. However, if any code uses unsafe, it is the responsibility
of the programmer to ensure that the program is memory safe—and if the programmer fails to
do so, then the behavior of the program is undefined (by definition).
In practice, of course, most code does use unsafe, albeit only indirectly.
Most code relies on low-level utilities that can only be implemented with unsafe code,
including many from the standard library (e.g., Arc, RefCell, and so on), but also
from user-provided crates. In any case, the Rust philosophy is that the providers of these
low-level utilities should meet a standard of “unsafe encapsulation.”
A programmer interacting using the library only through its safe API (and also not using
unsafe code anywhere else) should not be able to exhibit undefined behavior,
not even by writing buggy code or using the API is an unintended way.
As such, the library implementors need to code defensively against all possible ways the
client might use the safe API.
When they are successful in this, the clients once again gain the guarantee that they
cannot invoke UB without unsafe code.
By contrast, Verus does not have an “unsafe/safe” distinction, nor does it have a notion of unsafe encapsulation. This is because it verifies both memory safety and other forms of correctness through Verus specifications.
Example
Consider, for example, the index operation in Rust’s standard Vec container.
If the client calls this function with an index that is not in-range for the vector’s
length, then it is likely a bug on the part of the client. However, the index operation
is part of the safe API, and therefore it must be robust to such things, and it can never
attempt to read out-of-bounds memory. Therefore, the implementation of this operation has
to do a bounds check (panicking if the bounds check fails).
On the other hand, consider this (possible) implementation of index for Verus’s
Vec collection:
impl<A> Vec<A> {
#[verifier::external_body]
pub fn index(&self, i: usize) -> (r: &A)
requires
i < self.len(),
ensures
*r === self[i as int],
{
unsafe { self.vec.get_unchecked(i) }
}
}Unlike Rust’s index, this implementation has no bounds checks, and it exhibits UB if called
for a value of i that is out-of-bounds. Therefore, as ordinary Rust, it would not meet
the standards of unsafe encapsulation.
However, due to its requires clause,
Verus enforces that any call to this function will satisfy the contract and be in-bounds.
Therefore, UB cannot occur in a verified Verus program, but type-checking alone is not
sufficient to ensure this.
Conclusion
Rust’s concept of unsafe encapsulation means that programmers writing in safe Rust can be sure that their programs will be memory safe as long as they type-check and pass the borrow-checker, even if their code otherwise has bugs.
In Verus, there is no staggered notion of correctness. If the program verifies, then it is memory safe, and it will execute according to all its specifications. If the program fails to verify, then all bets are off.
Calling verified code from unverified code
Of course, the correctness of Verus code depends on meeting the assumptions as provided in its specification. If you call verified code from unverified code, Verus won’t be able to check that these contracts are upheld at each call-site, so the responsibility is on the developer to meet them.
The developer needs to meet these assumptions:
- Any
requiresclauses on the function being called - Any trait implementation used to meet the function’s trait bounds are implemented according to the trait specifications.
Let me give an example of the latter. Suppose V is the verified source code, which declares
a trait Trait and a function with a trait bound, f<T: Trait>.
Also suppose Trait has a function trait_fn with an ensures clause.
Now suppose we have unverified source U, which defines a type X and a trait impl
impl Trait for X.
Then, in order for U to safely call f, the developer needs to make sure that
X::trait_fn correctly meets the ensures specification that V demands.
Requirements on the Drop trait
Note: We hope to simplify or remove this requirement in the future.
Note that the Drop trait has some special considerations. Specifically, Verus treats drop
as if it has the following signature:
fn drop(&mut self)
opens_invariants none
no_unwind
(See opens_invariants and no_unwind.)
For any verified implementation of Drop, Verus checks that it meets this criterion.
For unverified implementations of drop, this onus is on the user to meet this criterion.
Warning
As discussed in the last chapter, the memory safety of a verified program is conditional on verification. Therefore, calling verified code from unverified code could be non-memory-safe if the unverified code fails to uphold these contracts.
IDE Support for Verus
Verus currently has IDE support for VS Code and Emacs.
For VS Code, we require verus-analyzer, our Verus-specific fork of rust-analyzer. To use Verus with VS Code, follow the instructions in the README for verus-analyzer.
For Emacs, we have stand-alone support for Verus. The steps to get started with Emacs are below.
Quickstart Emacs
We support for Verus programming in Emacs through verus-mode.el, a major mode that supports syntax highlighting, verification-on-save, jump-to-definition, and more.
To use verus-mode, the setup can be as simple as configuring .emacs to (i) set verus-home to the path to Verus, and then (ii) load up verus-mode.
For example, if you use use-package, you can clone verus-mode.el into a location that Emacs can load from, and add the following snippet:
(use-package verus-mode
:init
(setq verus-home "PATH_TO_VERUS_DIR")) ; Path to where you've cloned https://github.com/verus-lang/verus
Depending on your specific Emacs setup, your exact installation process for verus-mode.el could vary. Detailed installation steps for various Emacs setups are documented in the Install section on verus-mode.el’s README.
For more details on latest features, key-bindings, and troubleshooting tips, do check out the README for verus-mode.el.
Installing and configuring Singular
Singular must be installed in order to use the integer_ring solver mode.
Steps:
-
Install Singular
- To use Singular’s standard library, you need more than just the Singular executable binary.
Hence, when possible, we strongly recommend using your system’s package manager. Regardless of the method you select, please install Singular version 4.3.2: other versions are untested, and 4.4.0 is known to be incompatible with Verus. Here are
some suggested steps for different platforms.
-
Mac:
brew install Singularand set theVERUS_SINGULAR_PATHenvironment variable when running Verus. (e.g.VERUS_SINGULAR_PATH=/usr/local/bin/Singular). For more options, see Singular’s OS X installation guide. -
Debian-based Linux:
apt-get install singularand set theVERUS_SINGULAR_PATHenvironment variable when running Verus. (e.g.VERUS_SINGULAR_PATH=/usr/bin/Singular). For more options, see Singular’s Linux installation guide. -
Windows: See Singular’s Windows installation guide.
-
- To use Singular’s standard library, you need more than just the Singular executable binary.
Hence, when possible, we strongly recommend using your system’s package manager. Regardless of the method you select, please install Singular version 4.3.2: other versions are untested, and 4.4.0 is known to be incompatible with Verus. Here are
some suggested steps for different platforms.
-
Compiling Verus with Singular Support
- The
integer_ringfunctionality is conditionally compiled when thesingularfeature is set. To add this feature, add the--features singularflag when you invokevargo buildto compile Verus.
- The
Documentation with Rustdoc
Verus provides a tool to help make Verus specification look nice in rustdoc.
To do this, you first run rustdoc on a crate and then run an HTML postprocessor called
Verusdoc.
First, make sure verusdoc is built by running vargo build -p verusdoc in the
verus/source directory.
Unfortunately, we currently don’t have helpful tooling for running rustdoc with the
appropriate dependencies and flags, so you’ll need to set that up manually.
Here is an example:
VERUS=/path/to/verus/source
if [ `uname` == "Darwin" ]; then
DYN_LIB_EXT=dylib
elif [ `uname` == "Linux" ]; then
DYN_LIB_EXT=so
fi
# Run rustdoc.
# Note the VERUSDOC environment variable.
RUSTC_BOOTSTRAP=1 VERUSDOC=1 rustdoc \
--extern builtin=$VERUS/target-verus/debug/libbuiltin.rlib \
--extern builtin_macros=$VERUS/target-verus/debug/libbuiltin_macros.$DYN_LIB_EXT \
--extern state_machines_macros=$VERUS/target-verus/debug/libstate_machines_macros.$DYN_LIB_EXT \
--extern vstd=$VERUS/target-verus/debug/libvstd.rlib \
--edition=2021 \
--cfg verus_keep_ghost \
--cfg verus_keep_ghost_body \
--cfg 'feature="std"' \
--cfg 'feature="alloc"' \
'-Zcrate-attr=feature(register_tool)' \
'-Zcrate-attr=register_tool(verus)' \
'-Zcrate-attr=register_tool(verifier)' \
'-Zcrate-attr=register_tool(verusfmt)' \
--crate-type=lib \
./lib.rs
# Run the post-processor.
$VERUS/target/debug/verusdoc
If you run it with a file lib.rs like this:
#![allow(unused_imports)]
use builtin::*;
use builtin_macros::*;
use vstd::prelude::*;
verus!{
/// Computes the max
pub fn compute_max(x: u32, y: u32) -> (max: u32)
ensures max == (if x > y { x } else { y }),
{
if x < y {
y
} else {
x
}
}
}
It will generate rustdoc that looks like this:

Ghost Erasure
Verus performs ghost erasure: ghost code that exists for verification purposes is removed when building the executable artifacts, ensuring they are minimally disturbed.
One byproduct of this is that certain identifiers that exist at verification time will not exist at compile time. This means that the code shown below would fail to compile:
use vstd::prelude::*;
verus! {
pub mod ghost_mod {
pub closed spec fn ghost_fn() -> bool { true }
}
pub mod test_mod {
use crate::ghost_mod::ghost_fn;
// ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
// FAILS: During compilation, ghost_fn is erased, causing rustc
// to complain about a missing definition
pub fn exec_fn() -> u64 {
1
}
}To remedy this, Verus provides the verus_only flag, which is turned on during
verification, but is otherwise off. This allows us to guard use statements like the one above:
pub mod test_mod {
#[cfg(verus_only)]
use crate::ghost_mod::ghost_fn;
// ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
// OK: During compilation, the `use` statement is removed
}Anoter use-case for the verus_only flag is setting attributes that only make sense during verification.
For instance, the code below sets the verifier::loop_isolation option to false for the file, only if verus_only is set:
#![cfg_attr(verus_only, verus::loop_isolation(false))]Caution
This should only be used to guard
usestatements and setting config attributes. Using this feature flag for conditional compilation of code can introduce unsoundness, breaking the verification guarantees.As an example, the code below will verify successfully, even though it
f()returns 42 when running the executable.fn f() -> (u: u32) ensures u != 0 { #[cfg(verus_only)] { return 0; } #[cfg(not(verus_only))] { return 42; } }
Note
Verus is under active development meaning this option may change or be removed (in particular if a better solution to this problem is devised). See the Github discussion for more information.
Cargo.toml configuration
Since version 1.80, Rust automatically checks if all cfgs match expected config names.
The verus_only feature is passed in directly by Verus and never declared in a
Cargo.toml. This means that Rust will emit a warning when compiling. To prevent this, add the
following to your Cargo.toml:
[lints.rust]
unexpected_cfgs = { level = "warn", check-cfg = [
'cfg(verus_only)',
] }
Note
This is done automatically when initializing the repository with
cargo verus new
Supported Rust Features
Quick reference for supported Rust features. Note that this list does not include all Verus features, and Verus has many spec/proof features without any standard Rust equivalent—this list only concerns Rust features. See the guide for more information about Verus’ distinction between executable Rust code, specification code, and proof code.
Note that Verus is in active development. If a feature is unsupported, it might be genuinely hard, or it might just be low priority. See the github issues or discussions for information on planned features.
Last Updated: 2026-02-18
| Items | |
|---|---|
| Functions, methods, associated functions | Supported |
| Associated constants | Partially supported |
| Structs | Supported |
| Enums | Supported |
| Const functions | Partially supported |
| Async functions | Not supported |
| Macros | Supported |
| Type aliases | Supported |
| Const items | Partially supported |
| Static items | Partially supported |
| Struct/enum definitions | |
| Type parameters | Supported |
| Where clauses | Supported |
| Lifetime parameters | Supported |
| Const generics | Partially Supported |
| Custom discriminants | Supported |
| public / private fields | Partially supported |
| Expressions and Statements | |
| Variables, assignment, mut variables | Supported |
| If, else | Supported |
| patterns, match, if-let, match guards | Supported |
| Block expressions | Supported |
| Items | Not supported |
loop, while |
Supported |
for |
Partially supported |
? |
Supported |
| Async blocks | Not supported |
| await | Not supported |
| Unsafe blocks | Supported |
& |
Supported |
&mut, place expressions |
Partially supported |
==, != |
Supported |
Type cast (as) |
Partially supported |
Compound assigments (+=, etc.) |
Supported |
| Array expressions | Partially supported (no fill expressions with `const` arguments) |
| Range expressions | Supported |
| Index expressions | Partially supported |
| Tuple expressions | Supported |
| Struct/enum constructors | Supported |
| Field access | Supported |
| Function and method calls | Supported |
| Closures | Supported |
| Labels, break, continue | Supported |
| Return statements | Supported |
| Integer arithmetic | |
| Arithmetic for unsigned | Supported |
| Arithmetic for signed | Supported |
Bitwise operations (&, |, !, >>, <<) |
Supported |
Arch-dependent types (usize, isize) |
Supported |
| Types and standard library functionality | |
| Integer types | Supported |
bool |
Supported |
| Strings | Supported |
| Vec | Supported |
| Option / Result | Supported |
| Floating point | Partially supported |
| Slices | Supported |
| Arrays | Supported |
| Pointers | Partially supported |
References (&) |
Supported |
Mutable references (&mut) |
Partially supported |
| Never type | Supported |
| Function pointer types | Not supported |
| Closure types | Supported |
| Trait objects (dyn) | Partially supported |
| impl types | Partially supported |
| Cell, RefCell | Not supported (see vstd alternatives) |
| Iterators | Partially supported |
Vec, HashMap, HashSet, VecDeque |
Supported |
Smart pointers (Box, Rc, Arc) |
Supported |
Pin |
Not supported |
| Hardware intrinsics | Not supported |
| Printing, I/O | Not supported |
| Panic-unwinding | Partially supported |
| Traits | |
| User-defined traits | Supported |
| Default implementations | Supported |
| Trait bounds on trait declarations | Supported |
| Traits with type arguments | Supported |
| Associated types | Supported |
| Generic associated types | Partially supported (only lifetimes are supported) |
| Higher-ranked trait bounds | Supported |
Marker traits (Copy, Send, Sync) |
Supported |
Standard traits (Clone, Default, Step, From, TryFrom, Into, PartialEq, Eq, PartialOrd, Ord, Neg, Not, Add, Sub, Mul, Div, Rem, BitAnd, BitOr, BitXor, Shl, Shr) |
Partially supported |
Standard traits (Debug, serde::Serialize) |
Not supported |
User-defined destructors (Drop) |
Not supported |
Sized (size_of, align_of) |
Supported |
Deref |
Supported |
DerefMut |
Not supported |
| Multi-threading | |
Mutex, RwLock (from standard library) |
Not supported |
| Verified lock implementations | Supported |
| Atomics | Supported (vstd equivalent) |
| spawn and join | Supported |
| Interior mutability | Supported |
| Unsafe | |
| Raw pointers | Partially supported |
| Transmute | Not supported |
| Unions | Supported |
UnsafeCell |
Supported (vstd equivalent) |
| Crates and code organization | |
| Multi-crate projects | Partially supported |
| Verified crate + unverified crates | Partially supported |
| Modules | Supported |
| rustdoc | Supported |
Verus Syntax
The code below illustrates a large swath of Verus’ syntax.
#![allow(unused_imports)]
use verus_builtin::*;
use verus_builtin_macros::*;
use vstd::{modes::*, prelude::*, seq::*, *};
fn main() {}
const EXTERNAL_C: u8 = 7;
fn external_f(u: u8) -> u8 {
u / 2
}
verus! {
/// functions may be declared exec (default), proof, or spec, which contain
/// exec code, proof code, and spec code, respectively.
/// - exec code: compiled, may have requires/ensures
/// - proof code: erased before compilation, may have requires/ensures
/// - spec code: erased before compilation, no requires/ensures, but may have recommends
/// exec and proof functions may name their return values inside parentheses, before the return type
fn my_exec_fun(x: u32, y: u32) -> (sum: u32)
requires
x < 100,
y < 100,
ensures
sum < 200,
{
x + y
}
proof fn my_proof_fun(x: int, y: int) -> (sum: int)
requires
x < 100,
y < 100,
ensures
sum < 200,
{
x + y
}
spec fn my_spec_fun(x: int, y: int) -> int
recommends
x < 100,
y < 100,
{
x + y
}
/// exec code cannot directly call proof functions or spec functions.
/// However, exec code can contain proof blocks (proof { ... }),
/// which contain proof code.
/// This proof code can call proof functions and spec functions.
fn test_my_funs(x: u32, y: u32)
requires
x < 100,
y < 100,
{
// my_proof_fun(x, y); // not allowed in exec code
// let u = my_spec_fun(x, y); // not allowed exec code
proof {
let u = my_spec_fun(x as int, y as int); // allowed in proof code
my_proof_fun(u / 2, y as int); // allowed in proof code
}
}
/// spec functions with pub or pub(...) must specify whether the body of the function
/// should also be made publicly visible (open function) or not visible (closed function).
pub open spec fn my_pub_spec_fun1(x: int, y: int) -> int {
// function and body visible to all
x / 2 + y / 2
}
/* TODO
pub open(crate) spec fn my_pub_spec_fun2(x: u32, y: u32) -> u32 {
// function visible to all, body visible to crate
x / 2 + y / 2
}
*/
// TODO(main_new) pub(crate) is not being handled correctly
// pub(crate) open spec fn my_pub_spec_fun3(x: int, y: int) -> int {
// // function and body visible to crate
// x / 2 + y / 2
// }
pub closed spec fn my_pub_spec_fun4(x: int, y: int) -> int {
// function visible to all, body visible to module
x / 2 + y / 2
}
pub(crate) closed spec fn my_pub_spec_fun5(x: int, y: int) -> int {
// function visible to crate, body visible to module
x / 2 + y / 2
}
/// Recursive functions must have decreases clauses so that Verus can verify that the functions
/// terminate.
fn test_rec(x: u64, y: u64)
requires
0 < x < 100,
y < 100 - x,
decreases x,
{
if x > 1 {
test_rec(x - 1, y + 1);
}
}
/// Multiple decreases clauses are ordered lexicographically, so that later clauses may
/// increase when earlier clauses decrease.
spec fn test_rec2(x: int, y: int) -> int
decreases x, y,
{
if y > 0 {
1 + test_rec2(x, y - 1)
} else if x > 0 {
2 + test_rec2(x - 1, 100)
} else {
3
}
}
/// To help prove termination, recursive spec functions may have embedded proof blocks
/// that can make assertions, use broadcasts, and call lemmas.
spec fn test_rec_proof_block(x: int, y: int) -> int
decreases x,
{
if x < 1 {
0
} else {
proof {
assert(x - 1 >= 0);
}
test_rec_proof_block(x - 1, y + 1) + 1
}
}
/// Decreases and recommends may specify additional clauses:
/// - decreases .. "when" restricts the function definition to a condition
/// that makes the function terminate
/// - decreases .. "via" specifies a proof function that proves the termination
/// (although proof blocks are usually simpler; see above)
/// - recommends .. "when" specifies a proof function that proves the
/// recommendations of the functions invoked in the body
spec fn add0(a: nat, b: nat) -> nat
recommends
a > 0,
via add0_recommends
{
a + b
}
spec fn dec0(a: int) -> int
decreases a,
when a > 0
via dec0_decreases
{
if a > 0 {
dec0(a - 1)
} else {
0
}
}
#[via_fn]
proof fn add0_recommends(a: nat, b: nat) {
// proof
}
#[via_fn]
proof fn dec0_decreases(a: int) {
// proof
}
/// variables may be exec, tracked, or ghost
/// - exec: compiled
/// - tracked: erased before compilation, checked for lifetimes (advanced feature, discussed later)
/// - ghost: erased before compilation, no lifetime checking, can create default value of any type
/// Different variable modes may be used in different code modes:
/// - variables in exec code are always exec
/// - variables in proof code are ghost by default (tracked variables must be marked "tracked")
/// - variables in spec code are always ghost
/// For example:
fn test_my_funs2(
a: u32, // exec variable
b: u32, // exec variable
)
requires
a < 100,
b < 100,
{
let s = a + b; // s is an exec variable
proof {
let u = a + b; // u is a ghost variable
my_proof_fun(u / 2, b as int); // my_proof_fun(x, y) takes ghost parameters x and y
}
}
/// assume and assert are treated as proof code even outside of proof blocks.
/// "assert by" may be used to provide proof code that proves the assertion.
#[verifier::opaque]
spec fn f1(i: int) -> int {
i + 1
}
fn assert_by_test() {
assert(f1(3) > 3) by {
reveal(f1); // reveal f1's definition just inside this block
}
assert(f1(3) > 3);
}
/// "assert by" can also invoke specialized provers for bit-vector reasoning or nonlinear arithmetic.
fn assert_by_provers(x: u32) {
assert(x ^ x == 0u32) by (bit_vector);
assert(2 <= x && x < 10 ==> x * x > x) by (nonlinear_arith);
}
/// "assert by" provers can also appear on function signatures to select a specific prover
/// for the function body.
proof fn lemma_mul_upper_bound(x: int, x_bound: int, y: int, y_bound: int)
by (nonlinear_arith)
requires
x <= x_bound,
y <= y_bound,
0 <= x,
0 <= y,
ensures
x * y <= x_bound * y_bound,
{
}
/// "assert by" can use nonlinear_arith with proof code,
/// where "requires" clauses selectively make facts available to the proof code.
proof fn test5_bound_checking(x: u32, y: u32, z: u32)
requires
x <= 0xffff,
y <= 0xffff,
z <= 0xffff,
{
assert(x * z == mul(x, z)) by (nonlinear_arith)
requires
x <= 0xffff,
z <= 0xffff,
{
assert(0 <= x * z);
assert(x * z <= 0xffff * 0xffff);
}
}
/// The syntax for forall and exists quantifiers is based on closures:
fn test_quantifier() {
assert(forall|x: int, y: int| 0 <= x < 100 && 0 <= y < 100 ==> my_spec_fun(x, y) >= x);
assert(my_spec_fun(10, 20) == 30);
assert(exists|x: int, y: int| my_spec_fun(x, y) == 30);
}
/// "assert forall by" may be used to prove foralls:
fn test_assert_forall_by() {
assert forall|x: int, y: int| f1(x) + f1(y) == x + y + 2 by {
reveal(f1);
}
assert(f1(1) + f1(2) == 5);
assert(f1(3) + f1(4) == 9);
// to prove forall|...| P ==> Q, write assert forall|...| P implies Q by {...}
assert forall|x: int| x < 10 implies f1(x) < 11 by {
assert(x < 10);
reveal(f1);
assert(f1(x) < 11);
}
assert(f1(3) < 11);
}
/// To extract ghost witness values from exists, use choose:
fn test_choose() {
assume(exists|x: int| f1(x) == 10);
proof {
let x_witness = choose|x: int| f1(x) == 10;
assert(f1(x_witness) == 10);
}
assume(exists|x: int, y: int| f1(x) + f1(y) == 30);
proof {
let (x_witness, y_witness): (int, int) = choose|x: int, y: int| f1(x) + f1(y) == 30;
assert(f1(x_witness) + f1(y_witness) == 30);
}
}
/// To manually specify a trigger to use for the SMT solver to match on when instantiating a forall
/// or proving an exists, use #[trigger]:
fn test_single_trigger1() {
// Use [my_spec_fun(x, y)] as the trigger
assume(forall|x: int, y: int| f1(x) < 100 && f1(y) < 100 ==> #[trigger] my_spec_fun(x, y) >= x);
}
fn test_single_trigger2() {
// Use [f1(x), f1(y)] as the trigger
assume(forall|x: int, y: int| #[trigger]
f1(x) < 100 && #[trigger] f1(y) < 100 ==> my_spec_fun(x, y) >= x);
}
/// To manually specify multiple triggers, use #![trigger]:
fn test_multiple_triggers() {
// Use both [my_spec_fun(x, y)] and [f1(x), f1(y)] as triggers
assume(forall|x: int, y: int|
#![trigger my_spec_fun(x, y)]
#![trigger f1(x), f1(y)]
f1(x) < 100 && f1(y) < 100 ==> my_spec_fun(x, y) >= x);
}
/// Verus can often automatically choose a trigger if no manual trigger is given.
/// Use the command-line option --triggers to print the chosen triggers.
fn test_auto_trigger1() {
// Verus automatically chose [my_spec_fun(x, y)] as the trigger.
// (It considers this safer, i.e. likely to match less often, than the trigger [f1(x), f1(y)].)
assume(forall|x: int, y: int| f1(x) < 100 && f1(y) < 100 ==> my_spec_fun(x, y) >= x);
}
/// If Verus prints a note saying that it automatically chose a trigger with low confidence,
/// you can supply manual triggers or use #![auto] to accept the automatically chosen trigger.
fn test_auto_trigger2() {
// Verus chose [f1(x), f1(y)] as the trigger; go ahead and accept that
assume(forall|x: int, y: int| #![auto] f1(x) < 100 && f1(y) < 100 ==> my_spec_fun(3, y) >= 3);
}
/// &&& and ||| are like && and ||, but have low precedence (lower than all other binary operators,
/// and lower than forall/exists/choose).
/// &&& must appear before each conjunct, rather than between the conjuncts (similarly for |||).
/// &&& must appear directly inside a block or at the end of a block.
spec fn simple_conjuncts(x: int, y: int) -> bool {
&&& 1 < x
&&& y > 9 ==> x + y < 50
&&& x < 100
&&& y < 100
}
spec fn complex_conjuncts(x: int, y: int) -> bool {
let b = x < y;
&&& b
&&& if false {
&&& b ==> b
&&& !b ==> !b
} else {
||| b ==> b
||| !b
}
&&& false ==> true
}
/// ==> associates to the right, while <== associates to the left.
/// <==> is nonassociative.
/// == is SMT equality.
/// != is SMT disequality.
pub(crate) proof fn binary_ops<A>(a: A, x: int) {
assert(false ==> true);
assert(true && false ==> false && false);
assert(!(true && (false ==> false) && false));
assert(false ==> false ==> false);
assert(false ==> (false ==> false));
assert(!((false ==> false) ==> false));
assert(false <== false <== false);
assert(!(false <== (false <== false)));
assert((false <== false) <== false);
assert(2 + 2 !== 3);
assert(a == a);
assert(false <==> true && false);
}
/// In specs, <=, <, >=, and > may be chained together so that, for example, a <= b < c means
/// a <= b && b < c. (Note on efficiency: if b is a complex expression,
/// Verus will automatically introduce a temporary variable under the hood so that
/// the expression doesn't duplicate b: {let x_b = b; a <= x_b && x_b < c}.)
proof fn chained_comparisons(i: int, j: int, k: int)
requires
0 <= i + 1 <= j + 10 < k + 7,
ensures
j < k,
{
}
/// In specs, e@ is an abbreviation for e.view()
/// Many types implement a view() method to get an abstract ghost view of a concrete type.
fn test_views() {
let mut v: Vec<u8> = Vec::new();
v.push(10);
v.push(20);
proof {
let s: Seq<u8> = v@; // v@ is equivalent to v.view()
assert(s[0] == 10);
assert(s[1] == 20);
}
}
/// struct and enum declarations may be declared exec (default), tracked, or ghost,
/// and fields may be declared exec (default), tracked or ghost.
tracked struct TrackedAndGhost<T, G>(tracked T, ghost G);
/// Proof code may manipulate tracked variables directly.
/// Declarations of tracked variables must be explicitly marked as "tracked".
proof fn consume(tracked x: int) {
}
proof fn test_tracked(
tracked w: int,
tracked x: int,
tracked y: int,
z: int,
) -> tracked TrackedAndGhost<(int, int), int> {
consume(w);
let tracked tag: TrackedAndGhost<(int, int), int> = TrackedAndGhost((x, y), z);
let tracked TrackedAndGhost((a, b), c) = tag;
TrackedAndGhost((a, b), c)
}
/// Variables in exec code may be exec, ghost, or tracked.
fn test_ghost(x: u32, y: u32)
requires
x < 100,
y < 100,
{
let ghost u: int = my_spec_fun(x as int, y as int);
let ghost mut v = u + 1;
assert(v == x + y + 1);
proof {
v = v + 1; // proof code may assign to ghost mut variables
}
let ghost w = {
let temp = v + 1;
temp + 1
};
assert(w == x + y + 4);
}
/// Variables in exec code may be exec, ghost, or tracked.
/// However, exec function parameters and return values are always exec.
/// In these places, the library types Ghost and Tracked are used
/// to wrap ghost values and tracked values.
/// Ghost and tracked expressions Ghost(expr) and Tracked(expr) create values of type Ghost<T>
/// and Tracked<T>, where expr is treated as proof code whose value is wrapped inside Ghost or Tracked.
/// The view x@ of a Ghost or Tracked x is the ghost or tracked value inside the Ghost or Tracked.
fn test_ghost_wrappers(x: u32, y: Ghost<u32>)
requires
x < 100,
y@ < 100,
{
// Ghost(...) expressions can create values of type Ghost<...>:
let u: Ghost<int> = Ghost(my_spec_fun(x as int, y@ as int));
let mut v: Ghost<int> = Ghost(u@ + 1);
assert(v@ == x + y@ + 1);
proof {
v@ = v@ + 1; // proof code may assign to the view of exec variables of type Ghost/Tracked
}
let w: Ghost<int> = Ghost(
{
// proof block that returns a ghost value
let temp = v@ + 1;
temp + 1
},
);
assert(w@ == x + y@ + 4);
}
fn test_consume(t: Tracked<int>)
requires
t@ <= 7,
{
proof {
let tracked x = t.get();
assert(x <= 7);
consume(x);
}
}
/// Ghost(...) and Tracked(...) patterns can unwrap Ghost<...> and Tracked<...> values:
fn test_ghost_unwrap(
x: u32,
Ghost(y): Ghost<u32>,
) // unwrap so that y has typ u32, not Ghost<u32>
requires
x < 100,
y < 100,
{
// Ghost(u) pattern unwraps Ghost<...> values and gives u and v type int:
let Ghost(u): Ghost<int> = Ghost(my_spec_fun(x as int, y as int));
let Ghost(mut v): Ghost<int> = Ghost(u + 1);
assert(v == x + y + 1);
proof {
v = v + 1; // assign directly to ghost mut v
}
let Ghost(w): Ghost<int> = Ghost(
{
// proof block that returns a ghost value
let temp = v + 1;
temp + 1
},
);
assert(w == x + y + 4);
}
struct S {}
/// Exec code can use "let ghost" and "let tracked" to create local ghost and tracked variables.
/// Exec code can extract individual ghost and tracked values from Ghost and Tracked wrappers
/// with "let ...Ghost(x)..." and "let ...Tracked(x)...".
fn test_ghost_tuple_match(t: (Tracked<S>, Tracked<S>, Ghost<int>, Ghost<int>)) -> Tracked<S> {
let ghost g: (int, int) = (10, 20);
assert(g.0 + g.1 == 30);
let ghost (g1, g2) = g;
assert(g1 + g2 == 30);
// b1, b2: Tracked<S> and g3, g4: Ghost<int>
let (Tracked(b1), Tracked(b2), Ghost(g3), Ghost(g4)) = t;
Tracked(b2)
}
/// Exec code can Ghost(...) or Tracked(...) unwrapped parameter
/// to create a mutable ghost or tracked parameter:
fn test_ghost_mut(Ghost(g): Ghost<&mut int>)
ensures
*g == *old(g) + 1,
{
proof {
*g = *g + 1;
}
}
fn test_call_ghost_mut() {
let ghost mut g = 10int;
test_ghost_mut(Ghost(&mut g));
assert(g == 11);
}
/// Spec functions are not checked for correctness (although they are checked for termination).
/// However, marking a spec function as "spec(checked)" enables lightweight "recommends checking"
/// inside the spec function.
spec(checked) fn my_spec_fun2(x: int, y: int) -> int
recommends
x < 100,
y < 100,
{
// Because of spec(checked), Verus checks that my_spec_fun's recommends clauses are satisfied here:
my_spec_fun(x, y)
}
/// Spec functions may omit their body, in which case they are considered
/// uninterpreted (returning an arbitrary value of the return type depending on the input values).
/// This is safe, since spec functions (unlike proof and exec functions) may always
/// return arbitrary values of any type,
/// where the value may be special "bottom" value for otherwise uninhabited types.
uninterp spec fn my_uninterpreted_fun1(i: int, j: int) -> int;
uninterp spec fn my_uninterpreted_fun2(i: int, j: int) -> int
recommends
0 <= i < 10,
0 <= j < 10,
;
/// Trait functions may have specifications
trait T {
proof fn my_function_decl(&self, i: int, j: int) -> (r: int)
requires
0 <= i < 10,
0 <= j < 10,
ensures
i <= r,
j <= r,
;
/// A trait function may have a default (provided) implementation,
/// and this default may have additional ensures specified with default_ensures
fn my_function_with_a_default(&self, i: u32, j: u32) -> (r: u32)
requires
0 <= i < 10,
0 <= j < 10,
ensures
i <= r,
j <= r,
default_ensures
i == r || j == r,
{
if i >= j { i } else { j }
}
}
struct S1;
struct S2;
/// An impl can choose to use the default impl of my_function_with_a_default,
/// in which case the default_ensures applies to my_function_with_a_default
impl T for S1 {
proof fn my_function_decl(&self, i: int, j: int) -> (r: int) {
i + j
}
}
/// An impl can choose not to use the default impl of my_function_with_a_default,
/// and instead provide its own impl, in which case the default_ensures is ignored
impl T for S2 {
proof fn my_function_decl(&self, i: int, j: int) -> (r: int) {
i + j
}
fn my_function_with_a_default(&self, i: u32, j: u32) -> (r: u32)
ensures
r == i + j,
{
i + j
}
}
enum ThisOrThat {
This(nat),
That { v: int },
}
proof fn uses_is(t: ThisOrThat) {
match t {
ThisOrThat::This(..) => {
assert(t is This);
assert(t !is That);
},
ThisOrThat::That { .. } => {
assert(t is That);
assert(t !is This);
},
}
}
proof fn uses_arrow_matches_1(t: ThisOrThat)
requires
t is That ==> t->v == 3,
t is This ==> t->0 == 4,
{
assert(t matches ThisOrThat::This(k) ==> k == 4);
assert(t matches ThisOrThat::That { v } ==> v == 3);
}
proof fn uses_arrow_matches_2(t: ThisOrThat)
requires
t matches ThisOrThat::That { v: a } && a == 3,
{
assert(t is That && t->v == 3);
}
proof fn uses_spec_has(s: Set<int>, ms: vstd::multiset::Multiset<int>)
requires
s has 3,
ms has 4,
{
assert(s has 3);
assert(s has 3 == s has 3);
assert(ms has 4);
assert(ms has 4 == ms has 4);
}
proof fn broadcast_use() {
// you can use broadcase use on the module level, in proof functions,
// in proof blocks, or in assert-by
broadcast use vstd::seq_lib::group_seq_properties;
// you can also use multiple broadcast lemmas at once
broadcast use {
vstd::multiset::group_multiset_properties,
vstd::multiset::group_multiset_axioms,
};
// although we don't support a list of paths with common prefix like:
// broadcast use vstd::multiset::{group_multiset_properties, group_multiset_axioms};
assert forall|s: Seq<usize>, v: usize, x: usize|
{ s.contains(x) ==> s.push(v).contains(x) } by {
broadcast use vstd::seq_lib::group_seq_properties;
};
}
/// Specifications can be assumed for functions and constants from outside Verus.
/// Warning: such specifications are trusted to be correct, so they must be chosen carefully.
assume_specification[EXTERNAL_C] -> u8
returns
7u8,
;
assume_specification[external_f](u: u8) -> (r: u8)
ensures
r <= u,
;
fn test_external() {
assert(EXTERNAL_C == 7);
let x = external_f(10);
assert(x <= 10);
}
} // verus!Variable modes
In addition to having three function modes, Verus has three variable modes: exec, tracked, and ghost. Only exec variables exist in the compiled code, while ghost and tracked variables are “erased” from the compiled code.
See this tutorial page for an introduction to the concept of modes. The tracked mode is an advanced feature, and is discussed more in the concurrency guide.
Variable modes and function modes
Which variables are allowed depends on the expression mode, according to the following table:
| Default variable mode | ghost variables | tracked variables | exec variables | |
|---|---|---|---|---|
| spec code | ghost | yes | ||
| proof code | ghost | yes | yes | |
| exec code | exec | yes | yes | yes |
Although exec code allows variables of any mode, there are some restrictions; see below.
Using tracked and ghost variables from a proof function.
By default, any variable in a proof function has ghost mode. Parameters, variables,
and return values may be marked tracked. For example:
fn some_proof_fn(tracked param: Foo) -> (tracked ret: RetType) {
let tracked x = ...;
}For return values, the tracked keyword can only apply to the entire return type.
It is not possible to selectively apply tracked to individual elements of a tuple,
for example.
To mix-and-match tracked and ghost data, there are a few possibilities.
First, you can create a struct
marked tracked, which individual fields either marked ghost or tracked.
Secondly, you can use the Tracked and Ghost types from Verus’s builtin library to
create tuples like (Tracked<X>, Ghost<Y>). These support pattern matching:
proof fn some_call() -> (tracked ret: (Tracked<X>, Ghost<Y>)) { ... }
proof fn example() {
// The lower-case `tracked` keyword is used to indicate the right-hand side
// has `proof` mode, in order to allow the `tracked` call.
// The upper-case `Tracked` and `Ghost` are used in the pattern matching to unwrap
// the `X` and `Y` objects.
let tracked (Tracked(x), Ghost(y)) = some_call();
}Using tracked and ghost variables from an exec function.
Variables in exec code may be marked tracked or ghost. These variables will be erased
when the code is compiled. However, there are some restrictions.
In particular, variables marked tracked or ghost may be declared anywhere in an exec block. However, such variables may only be assigned to from inside a proof { ... } block.
fn some_exec_fn() {
let ghost mut x = 5; // this is allowed
proof {
x = 7; // this is allowed
}
x = 9; // this is not allowed
}Futhermore:
-
Arguments and return values for an
execfunction must beexecmode. -
Struct fields of an
execstruct must beexecmode.
To work around these, programs can use the Tracked and Ghost types.
Like in proof code, Verus supports pattern-matching for these types.
exec fn example() {
// Because of the keyword `tracked`, Verus interprets the right-hand side
// as if it were in a `proof` block.
let tracked (Tracked(x), Ghost(y)) = some_call();
}To handle parameters that must be passed via Tracked or Ghost types,
you can unwrap them via pattern matching:
exec fn example(Tracked(x): Tracked<X>, Ghost(y): Ghost<Y>) {
// Use `x` as if it were declared `let tracked x`
// Use `y` as if it were declared `let tracked y`
}Cheat sheet
Proof function, take tracked or ghost param
proof fn example(tracked x: X, ghost y: Y)To call this function from proof code:
proof fn test(tracked x: X, ghost y: Y) {
example(x, y);
}To call this function from exec code:
fn test() {
let tracked x = ...;
let ghost y = ...;
// From a proof block:
proof { example(x, y); }
}Proof function, return ghost param
proof fn example() -> (ret: Y)To call this function from proof code:
proof fn test() {
let y = example();
}To call this function from exec code:
fn test() {
let ghost y = example();
}Proof function, return tracked param
proof fn example() -> (tracked ret: X)To call this function from proof code:
proof fn test() {
let tracked y = example();
}To call this function from exec code:
fn test() {
// In a proof block:
proof { let tracked y = example(); }
// Or outside a proof block:
let tracked y = example();
}Proof function, return both a ghost param and tracked param
proof fn example() -> (tracked ret: (Tracked<X>, Ghost<Y>))To call this function from proof code:
proof fn test() {
let tracked (Tracked(x), Ghost(y)) = example();
}To call this function from exec code:
fn test() {
// In a proof block:
proof { let tracked (Tracked(x), Ghost(y)) = example(); }
// or outside a proof block:
let tracked (Tracked(x), Ghost(y)) = example();
}Exec function, take a tracked and ghost parameter:
fn example(Tracked(x): Tracked<X>, Ghost(y): Ghost<Y>)To call this function from exec code:
fn test() {
let tracked x = ...;
let ghost y = ...;
example(Tracked(x), Ghost(y));
}Exec function, return a tracked and ghost value:
fn example() -> (Tracked<X>, Ghost<Y>)To call this function from exec code:
fn test() {
let (Tracked(x), Ghost(y)) = example();
}Exec function, take a tracked parameter that is a mutable reference:
fn example(Tracked(x): Tracked<&mut X>)To call this function from exec code:
fn test() {
let tracked mut x = ...;
example(Tracked(&mut x));
}Contributed Extensions
The Verus community has contributed a number of extensions. Some of these extensions are not complete, in the sense that they will not work for all Verus code, but when they apply, they can be quite handy.
Producing executable code from spec functions with the exec_spec_verified! and exec_spec_unverified! macros
When writing proofs in Verus, we occasionally need to implement some simple function or data structure in both exec and spec modes, and then establish their equivalence. This process can be tedious for simple functions.
The exec_spec_verified! macro simplifies this process: you only need
to write the desired functions/structs/enums in spec mode within
the supported fragment of exec_spec_verified!, and then the macro can
automatically generate exec counterparts of these spec items,
as well as proofs of equivalence. These proofs also ensure termination,
the absence of arithmetic overflow, and the absence of precondition violations.
The exec_spec_unverified! macro also automatically compiles spec code to exec code,
but without proofs of equivalence. That is, all executable code with specifications
generated by exec_spec_unverified! is annotated with [verifier::external_body], so
the equivalence between the spec and the exec code is not proven by Verus.
The exec_spec_unverified! macro currently supports a larger fragment of Verus,
and is ideal for scenarios where the compiled code is not invoked in a verified project
(e.g., testing specifications on example inputs).
Skipping the proof generation sidesteps potential proof debugging in the
compiled exec code.
Unverified translations of vstd functions within the exec_spec_verified! and exec_spec_unverified! macros
To enable greater expressivity, the exec_spec_verified! and exec_spec_unverified! macros support the use of
several spec functions on types in vstd (such as Seq) within the macros. This means that exec
translations of supported spec functions are already provided by the macro. These translations
are used for compiling spec code which invokes such functions to exec code. The full list of
functions supported by each macro can be found below.
For many vstd functions, however, the translation from spec code to the exec equivalent is unverified.
Each case is marked clearly with a * below. We hope to reduce the number of unverified translations as Verus expands
its support for Rust language features.
The exec_spec_verified! macro
Here is an example:
use vstd::contrib::exec_spec::*;
use vstd::prelude::*;
verus! {
exec_spec_verified! {
struct Point {
x: i64,
y: i64,
}
spec fn on_line(points: Seq<Point>) -> bool {
forall |i: usize| #![auto] 0 <= i < points.len()
==> points[i as int].y == points[i as int].x
}
}
} // verus!In the example, we define a simple spec function on_line to check if
the given sequence of Points have the same coordinates.
The exec_spec_verified! macro call in this example takes all spec items in
its scope, and then derives executable counterparts along the lines of
the following definitions:
struct ExecPoint {
x: i64,
y: i64,
}
impl DeepView for ExecPoint {
type V = Point;
...
}
fn exec_on_line(points: &[ExecPoint]) -> (res: bool)
ensures res == on_line(points.deep_view())
{ ... }
After the macro invocation, we have the original spec items
as before (Point and on_line), but also new items ExecPoint and
exec_on_line with a suitable equivalence verified.
We can test the equivalence using the following sanity check:
verus! {
fn main() {
let p1 = ExecPoint { x: 1, y: 1 };
let p2 = ExecPoint { x: 2, y: 2 };
let points = vec![p1, p2];
assert(on_line(points.deep_view()));
let b = exec_on_line(points.as_slice());
assert(b);
}
} // verus!Currently, exec_spec_verified! supports these basic features:
- Basic arithmetic operations
- Logical operators (&&, ||, &&&, |||, not, ==>)
- If, match and “matches”
- Field expressions
- Spec function calls and recursion
- Bounded quantifiers of the form
forall |i: <type>| <lower> <op> i <op> <upper> ==> <expr>andexists |i: <type>| <lower> <op> i <op> <upper> && <expr>, where:<op>is either<=or<<type>is a Rust primitive integer (i<N>,isize,u<N>,usize)
SpecString(an alias toSeq<char>to syntactically indicate that we wantString/&str), equality*, indexing, len, string literalsOption<T>with these functions:- equality,
unwrap
- equality,
Seq<T>(compiled toVec<T>or&[T]depending on the context),seq!literals, and theseSeqfunctions:- equality*,
len, indexing,subrange*,add*,push*,update*,empty,to_multiset*,drop_first*,drop_last*,take*,skip*,first,last,is_suffix_of*,is_prefix_of*,contains*,index_of*,index_of_first*,index_of_last*
- equality*,
Map<K, V>(compiled toHashMap<K, V>), and theseMapfunctions:- equality*,
len*, indexing*,empty,dom*,insert*,remove*,get* - Note: indexing is only supported on
Map<K, V>whereKis a primitive type (e.g.usize); for other typesK, usegetinstead.
- equality*,
Set<T>(compiled toHashSet<T>), and theseSetfunctions:- equality*,
len*,empty,contains*,insert*,remove*,union*,intersect*,difference*
- equality*,
Multiset<T>(compiled toExecMultiset<T>, a type implemented invstd::contrib::exec_specwhose internal representation is aHashMap), and theseMultisetfunctions:- equality*,
len*,count*,empty*,singleton*,add*,sub*
- equality*,
- User-defined structs and enums. These types should be defined within the macro using spec-compatible types for the fields (e.g.
Seq). Such types are then compiled to theirExec-versions, which use the exec versions of each field’s type (e.g.Vec/slice). - Primitive integer/boolean types (
i<N>,isize,u<N>,usize,char, etc.). Note thatintandnatcannot be used inexec_spec_verified!orexec_spec_unverified!.
Functions marked with * have unverified translations from spec to exec code.
The exec_spec_unverified! macro
Here is the same example as above, but with the exec_spec_unverified! macro:
use vstd::contrib::exec_spec::*;
use vstd::prelude::*;
verus! {
exec_spec_unverified! {
struct Point {
x: i64,
y: i64,
}
spec fn on_line(points: Seq<Point>) -> bool {
forall |i: usize| #![auto] 0 <= i < points.len()
==> points[i as int].y == points[i as int].x
}
}
} // verus!The same exec items are generated as with the exec_spec_verified! macro,
except the specs on executable functions are not proven by Verus:
#[verifier::external_body]
fn exec_on_line(points: &[ExecPoint]) -> (res: bool)
ensures res == on_line(points.deep_view())
{ ... }
We can run the executable function exec_on_line to sanity check the output of
the compiled on_line spec on a specific input using the following:
fn main() {
let p1 = ExecPoint { x: 1, y: 1 };
let p2 = ExecPoint { x: 2, y: 2 };
let points = vec![p1, p2];
let b = exec_on_line(points.as_slice());
assert_eq!(b, true);
}The exec_spec_unverified! macro supports all of the same Verus features as exec_spec_verified!, as well as these additional features:
- More general bounded quantifiers. Quantifier expressions must match this form:
forall |x1: <type1>, x2: <type2>, ..., xN: <typeN>| <guard1> && <guard2> && ... && <guardN> ==> <body>orexists |x1: <type1>, x2: <type2>, ..., xN: <typeN>| <guard1> && <guard2> && ... && <guardN> && <body>, where:<guardI>is of the form:<lowerI> <op> xI <op> <upperI>, where:<op>is either<=or<<lowerI>and<upperI>can mentionxJfor allJ < I
<typeI>is a Rust primitive integer (i<N>,isize,u<N>,usize) orchar. Note thatcharis not supported by quantifiers inexec_spec_verified!.
Common errors
Indexing on Seq
When indexing on a Seq, the compilation process expects a usize which is cast to an int in the spec code.
The int cast will be removed by the compilation process, but it is necessary for the spec code to be accepted by Verus,
because Seq::index expects an int.
Here is a correct example:
pub open spec fn my_index(s: Seq<u8>, i: usize) -> u8
recommends 0 <= i < s.len()
{
s[i as int]
}
The following is incorrect because i is u64 instead of usize. This will result in a type error.
pub open spec fn my_index_err1(s: Seq<u8>, i: u64) -> u8
recommends 0 <= i < s.len()
{
s[i as int]
}
The following is incorrect because the compilation process expects that the index is cast to an int in the spec code.
This will also result in a type error.
pub open spec fn my_index_err2(s: Seq<u8>, i: usize) -> u8
recommends 0 <= i < s.len()
{
s[i]
}
Indexing on Map
To do indexing on a Map<K, V>, the key type K must be a primitive type.
Using a non-primitive for K will result in a type error when indexing is used.
As a workaround, use Map::get if a non-primitive type must be used for K.
The following is not supported by the macros:
pub struct Data {
x: usize
}
pub open spec fn my_index_err(m: Map<Data, u8>, i: Data) -> u8
recommends m.dom().contains(i)
{
m[i]
}
Use this instead:
pub struct Data {
x: usize
}
pub open spec fn my_index_map(m: Map<Data, u8>, i: Data) -> u8
recommends m.dom().contains(i)
{
m.get(i).unwrap()
}
Arithmetic operators
Due to the widening that Verus performs on arithmetic in spec code, an arithmetic expression (like a + b) may have a different type than its operands. This means that sometimes the type of an arithmetic expression is unsupported by the exec_spec_verified! and exec_spec_unverified! macros (i.e., int or nat), even if the types of both of the operands are supported (e.g., u64).
For example, the following will result in a type error, because for x: u64 and y: u64, Verus types x + y in spec code as an int.
pub open spec fn my_arith_err(x: u64, y: u64) -> u64
{
x + y
}
To fix this, you must cast the the result to u64:
pub open spec fn my_arith(x: u64, y: u64) -> u64
{
(x + y) as u64
}
Fully qualified paths
The exec_spec_verified! and exec_spec_unverified! macros do not currently support fully qualified paths, such as vstd::multiset::Multiset. To use types from another module, you should import the module at the top of the file and use the unqualified path (in this previous case, this would be Multiset). Using the fully qualified path will result in a type error.
Running code generated by exec_spec_unverified!
The exec_spec_unverified! macro does not generate Verus proofs for termination, the absence of arithmetic overflow, or the satisfaction of function preconditions within the compiled executable code. This differs from exec_spec_verified!. Instead, the code generated by exec_spec_unverified! will throw a runtime error if a precondition is violated (e.g. unwrapping a None) or if overflow occurs.
Related
exec_spec_verified! and exec_spec_unverified! compile spec items to exec items, which might not cover your use case.
For example, you may want to go from exec to spec,
or use the when_used_as_spec attribute.
Verus attributes for executable code
The #[verus_spec] attribute macro can help add Verus specifications and proofs
to existing executable code without sacrificing readability.
When to use #[verus_spec] instead of the verus! macro
The default way to write Verus code is by using the verus! macro. However,
using verus! to embed specifications and proofs directly in executable code
may not always be ideal for production settings. This is particularly true when
developers want to integrate verification into an existing Rust project and aim
to:
- Minimize changes to executable code — avoid modifying function APIs to include tracked or ghost arguments, and preserve native Rust syntax for maintainability.
- Adopt verification incrementally — apply Verus gradually to a large, existing codebase without requiring a full rewrite of the function APIs.
- Maintain readability — ensure the verified code remains clean and understandable for developers who are not familiar with Verus or want to ignore verification-related annotations.
- Optimize dependency management — use Verus components (
verus_builtin,verus_builtin_macros, andvstd) in a modular way, allowing projects to define custom stub macros and control Verus dependencies via feature flags.
Adding specifications to a function
Use #[verus_spec(requires ... ensures ...)] to attach a specification to a
function signature.
Here is an example:
#[verus_spec(sum =>
requires
x < 100,
y < 100,
ensures
sum < 200,
)]
fn my_exec_fun(x: u32, y: u32) -> u32
{
x + y
}Adding verification hints
Use #[verus_verify(...)] to provide hints to the verifier to mark a function
as external, external_body, spinoff_prover, or specify a different
resource limit via rlimit(amount).
In addition, you can create a dual mode (spec + exec) function the via
verus_verify(dual_spec) attribute, which will attempt to
generate a spec function from an executable function.
Adding proofs inside function
When a function has the #[verus_spec(...)] attribute, we can introduce
proofs directly inside executable functions using the proof macros described below.
When Rust builds the code (without using Verus), the #[verus_spec(...)] attribute will
ensure all proof code is erased.
Simple proof blocks
Use proof! to add a proof block; this is equivalent to using proof { ... }
inside the verus! macro. This implies that ghost/tracked variables defined inside
of proof! are local to that proof block and cannot be used in other proof blocks.
Ghost/Tracked variables across proof blocks
Use proof_decl! when you need to use ghost or tracked variables across different
proof blocks. It will allow you to introduce a proof block and declare function-scoped
ghost/tracked variables, as shown in this example:
#[verus_spec]
fn exec_with_proof() {
proof_decl!{
let ghost mut i = 0int;
assert(true);
}
test_for_loop(10);
proof!{
assert(i == 0);
}
}Adding ghost/tracked variables to executable function calls
-
#[verus_spec(with ...)]: Adds tracked or ghost variables as parameters or return values in an executable function.This generates two versions of the original function:
- A verified version (with ghost/tracked parameters), used in verified code.
- An unverified version (with the original signature), callable from unverified code.
-
proof_with!Works in combination withverus_specto pass tracked/ghost variables to a callee.When
proof_with!precedes a function call, the verified version is used; otherwise, the unverified version is chosen. The unverified version includes arequires falseprecondition, ensuring that improper use ofproof_with!will cause a verification failure when called from verified code.
Here is an example:
#[verus_spec(ret =>
with
Tracked(y): Tracked<&mut u32>,
Ghost(w): Ghost<u32>
-> z: Ghost<u32>
requires
x < 100,
*old(y) < 100,
ensures
*y == x,
ret == x + 1,
z@ == x,
)]
fn exec_tracked(x: u32) -> u32 {
proof! {
*y = x;
}
proof_with!(|= Ghost(x));
(x + 1)
}
#[verus_spec]
fn exec_tracked_test(x: u32) {
proof_decl!{
let ghost mut z = 0u32;
let tracked mut y = 0u32;
}
proof_with!{Tracked(&mut y), Ghost(0) => Ghost(z)}
let x = exec_tracked(1);
proof!{
assert(y == 1);
assert(z == 1);
assert(x == 2);
}
}
fn exec_external_test(x: u32) -> u32 {
exec_tracked(1)
}
Using a mix of #[verus_spec] and verus!
The preferred way to use #[verus_spec] and verus! is to use #[verus_spec]
for all executable functions, and use verus! for spec/proof functions.
NOTE: The combination of #[verus_spec(with ...)] + proof_with!
currently has compatibility issues with executable functions defined in verus!
if the functions involved receive or return ghost/tracked variables.
Specifically, proof_with! works with exec functions verified via
#[verus_spec]. Using proof_with! to pass ghost/tracked variables to an exec
function verified via verus! will result in this error:
[E0425]: cannot find function `_VERUS_VERIFIED_xxx` in this scope.
This is because verus! always requires a real change to the function’s
signature and has a single function definition, while #[verus_spec] expects a
verified and an unverified version of the function.
To use a function verified by verus!, a workaround is to create a trusted
wrapper function and then use it.
#[verus_verify(external_body)]
#[verus_spec(v =>
with Tracked(perm): Tracked<&mut PointsTo<T>>
requires
old(perm).ptr() == ptr,
old(perm).is_init(),
ensures
perm.ptr() == ptr,
perm.is_uninit(),
v == old(perm).value(),
)]
fn ptr_mut_read<'a, T>(ptr: *const T) -> T
{
vstd::raw_ptr::ptr_mut_read(ptr, Tracked::assume_new())
}
More examples and tests
#![feature(proc_macro_hygiene)]
#![allow(unused_imports)]
use verus_builtin::*;
use verus_builtin_macros::*;
use vstd::{modes::*, prelude::*, seq::*, *};
fn main() {}
/// functions may be declared exec (default), proof, or spec, which contain
/// exec code, proof code, and spec code, respectively.
/// - exec code: compiled, may have requires/ensures
/// - proof code: erased before compilation, may have requires/ensures
/// - spec code: erased before compilation, no requires/ensures, but may have recommends
/// exec and proof functions may name their return values inside parentheses, before the return type
#[verus_spec(sum =>
requires
x < 100,
y < 100,
ensures
sum < 200,
)]
fn my_exec_fun(x: u32, y: u32) -> u32
{
x + y
}
verus! {
proof fn my_proof_fun(x: int, y: int) -> (sum: int)
requires
x < 100,
y < 100,
ensures
sum < 200,
{
x + y
}
spec fn my_spec_fun(x: int, y: int) -> int
recommends
x < 100,
y < 100,
{
x + y
}
} // verus!
/// exec code cannot directly call proof functions or spec functions.
/// However, exec code can contain proof blocks (proof { ... }),
/// which contain proof code.
/// This proof code can call proof functions and spec functions.
#[verus_spec(
requires
x < 100,
y < 100,
)]
fn test_my_funs(x: u32, y: u32)
{
// my_proof_fun(x, y); // not allowed in exec code
// let u = my_spec_fun(x, y); // not allowed exec code
proof! {
let u = my_spec_fun(x as int, y as int); // allowed in proof code
my_proof_fun(u / 2, y as int); // allowed in proof code
}
}
verus! {
/// spec functions with pub or pub(...) must specify whether the body of the function
/// should also be made publicly visible (open function) or not visible (closed function).
pub open spec fn my_pub_spec_fun1(x: int, y: int) -> int {
// function and body visible to all
x / 2 + y / 2
}
/* TODO
pub open(crate) spec fn my_pub_spec_fun2(x: u32, y: u32) -> u32 {
// function visible to all, body visible to crate
x / 2 + y / 2
}
*/
// TODO(main_new) pub(crate) is not being handled correctly
// pub(crate) open spec fn my_pub_spec_fun3(x: int, y: int) -> int {
// // function and body visible to crate
// x / 2 + y / 2
// }
pub closed spec fn my_pub_spec_fun4(x: int, y: int) -> int {
// function visible to all, body visible to module
x / 2 + y / 2
}
pub(crate) closed spec fn my_pub_spec_fun5(x: int, y: int) -> int {
// function visible to crate, body visible to module
x / 2 + y / 2
}
} // verus!
/// Recursive functions must have decreases clauses so that Verus can verify that the functions
/// terminate.
#[verus_spec(
requires
0 < x < 100,
y < 100 - x,
decreases x,
)]
fn test_rec(x: u64, y: u64)
{
if x > 1 {
test_rec(x - 1, y + 1);
}
}
verus! {
/// Multiple decreases clauses are ordered lexicographically, so that later clauses may
/// increase when earlier clauses decrease.
spec fn test_rec2(x: int, y: int) -> int
decreases x, y,
{
if y > 0 {
1 + test_rec2(x, y - 1)
} else if x > 0 {
2 + test_rec2(x - 1, 100)
} else {
3
}
}
/// To help prove termination, recursive spec functions may have embedded proof blocks
/// that can make assertions, use broadcasts, and call lemmas.
spec fn test_rec_proof_block(x: int, y: int) -> int
decreases x,
{
if x < 1 {
0
} else {
proof {
assert(x - 1 >= 0);
}
test_rec_proof_block(x - 1, y + 1) + 1
}
}
/// Decreases and recommends may specify additional clauses:
/// - decreases .. "when" restricts the function definition to a condition
/// that makes the function terminate
/// - decreases .. "via" specifies a proof function that proves the termination
/// (although proof blocks are usually simpler; see above)
/// - recommends .. "when" specifies a proof function that proves the
/// recommendations of the functions invoked in the body
spec fn add0(a: nat, b: nat) -> nat
recommends
a > 0,
via add0_recommends
{
a + b
}
spec fn dec0(a: int) -> int
decreases a,
when a > 0
via dec0_decreases
{
if a > 0 {
dec0(a - 1)
} else {
0
}
}
#[via_fn]
proof fn add0_recommends(a: nat, b: nat) {
// proof
}
#[via_fn]
proof fn dec0_decreases(a: int) {
// proof
}
} // verus!
/// variables may be exec, tracked, or ghost
/// - exec: compiled
/// - tracked: erased before compilation, checked for lifetimes (advanced feature, discussed later)
/// - ghost: erased before compilation, no lifetime checking, can create default value of any type
/// Different variable modes may be used in different code modes:
/// - variables in exec code are always exec
/// - variables in proof code are ghost by default (tracked variables must be marked "tracked")
/// - variables in spec code are always ghost
/// For example:
#[verus_spec(
requires
a < 100,
b < 100,
)]
fn test_my_funs2(
a: u32, // exec variable
b: u32, // exec variable
)
{
let s = a + b; // s is an exec variable
proof! {
let u = a + b; // u is a ghost variable
my_proof_fun(u / 2, b as int); // my_proof_fun(x, y) takes ghost parameters x and y
}
}
verus! {
/// assume and assert are treated as proof code even outside of proof blocks.
/// "assert by" may be used to provide proof code that proves the assertion.
#[verifier::opaque]
spec fn f1(i: int) -> int {
i + 1
}
} // verus!
#[verus_spec()]
fn assert_by_test() {
proof! {
assert(f1(3) > 3) by {
reveal(f1); // reveal f1's definition just inside this block
}
assert(f1(3) > 3);
}
}
/// "assert by" can also invoke specialized provers for bit-vector reasoning or nonlinear arithmetic.
#[verus_spec()]
fn assert_by_provers(x: u32) {
proof! {
assert(x ^ x == 0u32) by (bit_vector);
assert(2 <= x && x < 10 ==> x * x > x) by (nonlinear_arith);
}
}
verus! {
/// "let ghost" currently requires the verus! macro
/// Variables in exec code may be exec, ghost, or tracked.
fn test_ghost(x: u32, y: u32)
requires
x < 100,
y < 100,
{
let ghost u: int = my_spec_fun(x as int, y as int);
let ghost mut v = u + 1;
assert(v == x + y + 1);
proof {
v = v + 1; // proof code may assign to ghost mut variables
}
let ghost w = {
let temp = v + 1;
temp + 1
};
assert(w == x + y + 4);
}
/// Ghost(...) expressions and patterns currently require the verus! macro
/// Ghost(...) and Tracked(...) patterns can unwrap Ghost<...> and Tracked<...> values:
fn test_ghost_unwrap(
x: u32,
Ghost(y): Ghost<u32>,
) // unwrap so that y has typ u32, not Ghost<u32>
requires
x < 100,
y < 100,
{
// Ghost(u) pattern unwraps Ghost<...> values and gives u and v type int:
let Ghost(u): Ghost<int> = Ghost(my_spec_fun(x as int, y as int));
let Ghost(mut v): Ghost<int> = Ghost(u + 1);
assert(v == x + y + 1);
proof {
v = v + 1; // assign directly to ghost mut v
}
let Ghost(w): Ghost<int> = Ghost(
{
// proof block that returns a ghost value
let temp = v + 1;
temp + 1
},
);
assert(w == x + y + 4);
}
} // verus!
/// Trait functions may have specifications
trait T {
#[verus_spec(r =>
requires
0 <= i < 10,
0 <= j < 10,
ensures
i <= r,
j <= r,
)]
fn my_uninterpreted_fun2(&self, i: u8, j: u8) -> u8;
}
#[verus_spec(ret =>
with
Tracked(y): Tracked<&mut u32>, Ghost(w): Ghost<u64> -> z: Ghost<u32>
requires
x < 100,
*old(y) < 100,
ensures
*y == x,
ret == x,
z == x,
)]
fn test_mut_tracked(x: u32) -> u32 {
proof!{
*y = x;
}
#[verus_spec(with |=Ghost(x))]
x
}
fn test_cal_mut_tracked(x: u32) {
proof_decl!{
let ghost mut z;
let tracked mut y = 0u32;
z = 0u32;
}
#[verus_spec(with Tracked(&mut y), Ghost(0) => Ghost(z))]
let _ = test_mut_tracked(0u32);
(#[verus_spec(with Tracked(&mut y), Ghost(0))]
test_mut_tracked(0u32));
return;
}#![feature(rustc_private)]
#[macro_use]
mod common;
use common::*;
test_verify_one_file_with_options! {
#[test] verus_verify_basic_while ["exec_allows_no_decreases_clause"] => code! {
#[verus_spec]
fn test1() {
let mut i = 0;
#[verus_spec(
invariant
i <= 10
)]
while i < 10
{
i = i + 1;
}
proof!{assert(i == 10);}
}
} => Ok(())
}
test_verify_one_file_with_options! {
#[test] verus_verify_basic_loop ["exec_allows_no_decreases_clause"] => code! {
#[verus_spec]
fn test1() {
let mut i = 0;
let mut ret = 0;
#[verus_spec(
invariant i <= 10,
invariant_except_break i <= 9,
ensures i == 10, ret == 10
)]
loop
{
i = i + 1;
if (i == 10) {
ret = i;
break;
}
}
proof!{assert(ret == 10);}
}
} => Ok(())
}
test_verify_one_file_with_options! {
#[test] verus_verify_basic_for_loop_verus_spec ["exec_allows_no_decreases_clause"] => code! {
use vstd::prelude::*;
#[verus_spec(v =>
ensures
v.len() == n,
forall|i: int| 0 <= i < n ==> v[i] == i
)]
fn test_for_loop(n: u32) -> Vec<u32>
{
let mut v: Vec<u32> = Vec::new();
#[verus_spec(
invariant
v@ =~= Seq::new(i as nat, |k| k as u32),
)]
for i in 0..n
{
v.push(i);
}
v
}
} => Ok(())
}
test_verify_one_file_with_options! {
#[test] verus_verify_for_loop_verus_spec_naming_iter ["exec_allows_no_decreases_clause"] => code! {
use vstd::prelude::*;
#[verus_spec(v =>
ensures
v.len() == n,
forall|i: int| 0 <= i < n ==> v[i] == 0
)]
fn test(n: u32) -> Vec<u32>
{
let mut v: Vec<u32> = Vec::new();
#[verus_spec(iter =>
invariant
v@ =~= Seq::new(iter.cur as nat, |k| 0u32),
)]
for _ in 0..n
{
v.push(0);
}
v
}
} => Ok(())
}
test_verify_one_file_with_options! {
#[test] verus_verify_basic_while_fail1 ["exec_allows_no_decreases_clause"] => code! {
#[verus_spec]
fn test1() {
let mut i = 0;
while i < 10 {
i = i + 1;
}
proof!{assert(i == 10);} // FAILS
}
} => Err(err) => assert_one_fails(err)
}
test_verify_one_file_with_options! {
#[test] basic_while_false_invariant ["exec_allows_no_decreases_clause"] => code! {
#[verus_verify]
fn test1() {
let mut i = 0;
#[verus_spec(
invariant
i <= 10, false
)]
while i < 10 {
i = i + 1;
}
}
} => Err(err) => assert_any_vir_error_msg(err, "invariant not satisfied before loop")
}
test_verify_one_file_with_options! {
#[test] verus_verify_invariant_on_func ["exec_allows_no_decreases_clause"] => code! {
#[verus_spec(
invariant true
)]
fn test1() {}
} => Err(err) => assert_any_vir_error_msg(err, "unexpected token")
}
test_verify_one_file! {
#[test] test_use_macro_attributes code!{
struct Abc<T> {
t: T,
}
trait SomeTrait {
#[verus_spec(ret =>
requires true
ensures ret
)]
fn f(&self) -> bool;
}
impl<S> Abc<S> {
fn foo(&self)
where S: SomeTrait
{
let ret = self.t.f();
proof!{assert(ret);}
}
}
} => Ok(())
}
test_verify_one_file! {
#[test] test_bad_macro_attributes_in_trait code!{
trait SomeTrait {
#[verus_spec(
ensures
true
)]
type T;
}
} => Err(err) => assert_any_vir_error_msg(err, "Misuse of #[verus_spec]")
}
test_verify_one_file_with_options! {
#[test] test_no_verus_verify_attributes_in_trait_impl ["--no-external-by-default"] => code!{
struct Abc<T> {
t: T,
}
#[verus_verify]
trait SomeTrait {
#[verus_spec(requires true)]
fn f(&self) -> bool;
}
impl<S> Abc<S> {
fn foo(&self)
where S: SomeTrait
{
let ret = self.t.f();
proof!{assert(ret);}
}
}
} => Err(err) => assert_vir_error_msg(err, "assertion failed")
}
test_verify_one_file! {
#[test] test_failed_ensures_macro_attributes code!{
#[verus_verify]
trait SomeTrait {
#[verus_spec(ret =>
requires true
ensures true, ret
)]
fn f(&self) -> bool;
}
#[verus_verify]
impl SomeTrait for bool {
fn f(&self) -> bool {
*self
}
}
} => Err(err) => assert_any_vir_error_msg(err, "postcondition not satisfied")
}
test_verify_one_file! {
#[test] test_default_fn_use_macro_attributes code!{
#[verus_verify]
struct Abc<T> {
t: T,
}
#[verus_verify]
trait SomeTrait {
#[verus_spec(ret =>
requires true
ensures ret
)]
fn f(&self) -> bool {
true
}
}
#[verus_verify]
impl<S> Abc<S> {
fn foo(&self)
where S: SomeTrait
{
let ret = self.t.f();
proof!{assert(ret);}
}
}
} => Ok(())
}
test_verify_one_file! {
#[test] test_default_failed_fn_use_macro_attributes code!{
#[verus_verify]
struct Abc<T> {
t: T,
}
#[verus_verify(rlimit(2))]
trait SomeTrait {
#[verus_spec(ret =>
requires true
ensures ret, !ret
)]
fn f(&self) -> bool {
true
}
}
} => Err(err) => assert_vir_error_msg(err, "postcondition not satisfied")
}
test_verify_one_file! {
#[test] test_external_body code!{
#[verus_verify(external_body)]
#[verus_spec(ret =>
requires true
ensures ret
)]
fn f() -> bool {
false
}
fn g() {
let r = f();
proof!{assert(r);}
}
} => Ok(())
}
test_verify_one_file! {
#[test] test_external_with_unsupported_features code!{
#[verus_verify(external)]
fn f<'a>(v: &'a mut [usize]) -> &'a mut usize {
unimplemented!()
}
} => Ok(())
}
test_verify_one_file! {
#[test] test_prover_attributes code!{
#[verus_verify(spinoff_prover, rlimit(2))]
#[verus_spec(
ensures
true
)]
fn test()
{}
} => Ok(())
}
test_verify_one_file! {
#[test] test_invalid_combination_attr code!{
#[verus_verify(external, spinoff_prover)]
fn f<'a>(v: &'a mut [usize]) -> &'a mut usize {
unimplemented!()
}
} => Err(e) => assert_any_vir_error_msg(e, "conflict parameters")
}
test_verify_one_file! {
#[test] test_proof_decl code!{
#[verus_spec]
fn f() {}
#[verus_spec]
fn test() {
proof!{
let x = 1 as int;
assert(x == 1);
}
proof_decl!{
let ghost mut x;
let tracked y = false;
x = 2int;
assert(!y);
if x == 1 {
assert(false);
}
}
f();
proof!{
assert(!y);
assert(x == 2);
}
}
} => Ok(())
}
test_verify_one_file! {
#[test] test_proof_decl_reject_exec code!{
#[verus_spec]
fn f() {}
#[verus_spec]
fn test() {
proof_decl!{
f();
}
f();
}
} => Err(e) => assert_vir_error_msg(e, "cannot call function `crate::f` with mode exec")
}
test_verify_one_file! {
#[test] test_proof_decl_reject_exec_local code!{
#[verus_spec]
fn test() {
proof_decl!{
let x = true;
}
}
} => Err(e) => assert_vir_error_msg(e, "Exec local is not allowed in proof_decl")
}
test_verify_one_file! {
#[test] test_with code!{
#[verus_spec(ret =>
with
Tracked(y): Tracked<&mut u32>,
Ghost(w): Ghost<u32>,
-> z: Ghost<u32>
requires
x < 100,
*old(y) < 100,
ensures
*y == x,
ret == x,
z@ == x,
)]
fn test_mut_tracked(x: u32) -> u32 {
proof!{
*y = x;
}
#[verus_spec(with |= Ghost(x))]
x
}
#[verus_spec]
fn test_call_mut_tracked(x: u32) {
proof_decl!{
let tracked mut y = 0u32;
}
{#[verus_spec(with Tracked(&mut y), Ghost(0) => _)]
test_mut_tracked(1);
};
if x < 100 && #[verus_spec(with Tracked(&mut y), Ghost(0) => _)]test_mut_tracked(x) == 0 {
return;
}
#[verus_spec(with Tracked(&mut y), Ghost(0) => Ghost(z))]
let _ = test_mut_tracked(1);
proof!{
assert(y == 1);
assert(z == 1);
}
}
} => Ok(())
}
test_verify_one_file! {
#[test] test_trait_signature code!{
trait X {
#[verus_spec(ret =>
with
Tracked(y): Tracked<&mut u32>,
Ghost(w): Ghost<u32>,
-> z: Ghost<u32>
)]
fn f(&self, x: u32) -> bool;
}
} => Err(e) => assert_any_vir_error_msg(e, "`with` does not support trait")
}
test_verify_one_file! {
#[test] test_unverified_code_signature code!{
#[verus_spec(ret =>
with
Tracked(y): Tracked<&mut u32>,
Ghost(w): Ghost<u32>,
-> z: Ghost<u32>
)]
fn test_mut_tracked(x: u32) -> u32 {
proof!{
*y = x;
}
#[verus_spec(with |= Ghost(x))]
x
}
#[verifier::external]
fn external_call_with_dummy(x: u32) -> u32 {
#[verus_spec(with Tracked::assume_new(), Ghost::assume_new() => _)]
test_mut_tracked(0)
}
#[verifier::external]
fn external_call_untouched(x: u32) -> u32 {
test_mut_tracked(0)
}
} => Ok(())
}
test_verify_one_file! {
#[test] test_verified_call_unverified_signature code!{
#[verus_spec(ret =>
with
Tracked(y): Tracked<&mut u32>,
Ghost(w): Ghost<u32>,
-> z: Ghost<u32>
)]
fn test_mut_tracked(x: u32) -> u32 {
proof!{
*y = x;
}
#[verus_spec(with |= Ghost(x))]
x
}
#[verus_spec]
fn verified_call_unverified(x: u32) {
test_mut_tracked(0); // FAILS
}
} => Err(e) => {
assert!(e.errors[0].rendered.contains("with"));
assert_one_fails(e)
}
}
test_verify_one_file! {
#[test] test_with2 code!{
#[verus_spec(ret =>
with
Tracked(y): Tracked<&mut u32>,
Ghost(w): Ghost<u32>,
-> z: Ghost<u32>
requires
x < 100,
*old(y) < 100,
ensures
*y == x,
ret == x,
z@ == x,
)]
fn test_mut_tracked(x: u32) -> u32 {
proof!{
*y = x;
}
#[verus_spec(with |= Ghost(x))]
x
}
#[verus_spec]
fn test_cal_mut_tracked(x: u32) {
proof_decl!{
let ghost mut z = 0u32;
let tracked mut y = 0u32;
}
if #[verus_spec(with Tracked(&mut y), Ghost(0) => Ghost(z))] test_mut_tracked(1) == 0 {
proof!{
assert(z == 1);
}
return;
}
proof!{
assert(y == 1);
}
}
} => Ok(())
}
test_verify_one_file! {
#[test] test_proof_with code!{
#[verus_spec(ret =>
with
Tracked(y): Tracked<&mut u32>,
Ghost(w): Ghost<u32>,
-> z: Ghost<u32>
requires
x < 100,
*old(y) < 100,
ensures
*y == x,
ret == x,
z@ == x,
)]
fn test_mut_tracked(x: u32) -> u32 {
proof!{
*y = x;
}
proof_with!{|= Ghost(x)}
x
}
#[verus_spec]
fn test_cal_mut_tracked(x: u32) {
proof_decl!{
let ghost mut z = 0u32;
let tracked mut y = 0u32;
}
if {
proof_with!{Tracked(&mut y), Ghost(0) => Ghost(z)} test_mut_tracked(1)
} == 0 {
proof!{
assert(z == 1);
}
return;
}
proof!{
assert(y == 1);
}
}
} => Ok(())
}
test_verify_one_file! {
#[test] test_proof_with_try code!{
use vstd::prelude::*;
#[verus_spec(
with Tracked(y): Tracked<&mut u32>
)]
fn f() -> Result<(), ()> {
Ok(())
}
#[verus_spec(
with Tracked(y): Tracked<&mut u32>
)]
fn test_try_call() -> Result<(), ()> {
proof_with!{Tracked(y)}
let _ = f()?;
Ok(())
}
} => Ok(())
}
test_verify_one_file! {
#[test] test_proof_with_err code!{
#[verus_spec]
fn test_mut_tracked(x: u32) -> u32 {
proof_declare!{
let ghost y = x;
}
proof_with!{Ghost(y)}
x
}
} => Err(e) => assert_any_vir_error_msg(e, "with ghost inputs/outputs cannot be applied to a non-call expression")
}
test_verify_one_file! {
#[test] test_dual_spec code!{
#[verus_verify(dual_spec(spec_f))]
#[verus_spec(
requires
x < 100,
y < 100,
returns f(x, y)
)]
fn f(x: u32, y: u32) -> u32 {
proof!{
assert(true);
}
{
proof!{assert(true);}
x + y
}
}
#[verus_verify(dual_spec)]
#[verus_spec(
requires
x < 100,
returns
f2(x),
)]
pub fn f2(x: u32) -> u32 {
f(x, 1)
}
#[verus_verify]
struct S;
impl S {
#[verus_verify(dual_spec)]
#[verus_spec(
returns
self.foo(x),
)]
fn foo(&self, x: u32) -> u32 {
x
}
}
verus!{
proof fn lemma_f(x: u32, y: u32)
requires
x < 100,
ensures
y == 1 ==> f(x, y) == f2(x),
f(x, y) == spec_f(x, y),
f2(x) == __VERUS_SPEC_f2(x),
f(x, y) == (x + y) as u32,
__VERUS_SPEC_f2(x) == x + 1,
{}
mod inner {
use super::*;
proof fn lemma_f(x: u32)
requires
x < 100,
ensures
f2(x) == __VERUS_SPEC_f2(x),
__VERUS_SPEC_f2(x) == (x + 1),
{}
}
}
} => Ok(())
}
test_verify_one_file! {
#[test] test_dual_spec_unsupported_body code!{
#[verus_verify(dual_spec(spec_f))]
#[verus_spec(
requires
*x < 100,
y < 100,
returns
f(x, y),
)]
fn f(x: &mut u32, y: u32) -> u32 {
*x = *x + y;
*x
}
} => Err(e) => assert_vir_error_msg(e, "&mut parameter not allowed for spec functions")
}
test_verify_one_file! {
#[test] test_dual_spec_unsupported_trait code!{
trait X {
fn f(&self) -> u32;
}
impl X for u32 {
#[verus_verify(dual_spec(spec_f))]
#[verus_spec(
ensures
self.spec_f(),
)]
fn f(&self) -> u32{
*self
}
}
} => Err(e) => assert_rust_error_msg(e, "method `spec_f` is not a member of trait `X`")
}
test_verify_one_file! {
#[test] test_macro_inside_proof_decl code!{
macro_rules! inline_proof {
($val: expr => $x: ident, $y: ident) => {
proof_decl!{
let tracked $x: int = $val;
let ghost $y: int = $val;
assert($x == $y);
}
}
}
fn test_inline_proof_via_macro() {
proof_decl!{
inline_proof!(0 => x, y);
assert(x == 0);
}
}
} => Ok(())
}
test_verify_one_file! {
#[test] basic_test code! {
use vstd::prelude::*;
fn testfn() {
let f =
#[verus_spec(z: u64 =>
requires y == 2
ensures z == 2
)]
|y: u64| { y };
proof!{
assert(f.requires((2,)));
assert(!f.ensures((2,),3));
}
let t = f(2);
proof!{
assert(t == 2);
}
}
} => Ok(())
}
test_verify_one_file! {
#[test] test_no_ret_fails code! {
use vstd::prelude::*;
fn testfn() {
let f =
#[verus_spec(
requires y == 2
)]
|y: u64| { };
}
} => Err(e) => assert_any_vir_error_msg(e, "Closure must have a return type")
}
test_verify_one_file! {
#[test] test_no_ret_ok code! {
use vstd::prelude::*;
fn testfn() {
let f1 =
#[verus_spec(
requires y == 2
)]
|y: u64| -> () { };
let f2 =
#[verus_spec(ret: () =>
requires y == 2
)]
|y: u64| { };
}
} => Ok(())
}
test_verify_one_file! {
#[test] test_const_fn_eval_via_proxy code!{
use vstd::prelude::*;
#[verus_spec(ret =>
ensures ret == x
)]
#[allow(unused_variables)]
pub const fn const_fn(x: u64) -> u64 {
proof!{
assert(true);
}
{
proof!{assert(true);}
}
x
}
pub const X: u64 = const_fn(1);
} => Ok(())
}
test_verify_one_file! {
#[test] test_const_fn_with_ghost code!{
use vstd::prelude::*;
#[verus_spec(ret =>
with Ghost(g): Ghost<u64>
)]
#[allow(unused_variables)]
pub const fn const_fn(x: u64) -> u64 {
proof!{
assert(true);
}
{
proof!{assert(true);}
}
x
}
#[verus_spec(
with Ghost(g): Ghost<u64>
)]
pub const fn call_const_fn(x: u64) -> u64 {
proof_with!{Ghost(g)}
const_fn(x)
}
// external call to const_fn does not need ghost var.
pub const X: u64 = const_fn(1);
} => Ok(())
}
test_verify_one_file! {
#[test] test_impl_method code!{
use vstd::prelude::*;
pub struct Foo;
#[verus_verify]
impl Foo {
#[verus_spec(ret =>
with
Tracked(c): Tracked<&mut ()>
requires
true,
ensures
ret == 1,
)]
fn test(a: u64, b: u64) -> u64 {
1
}
}
} => Ok(())
}
test_verify_one_file! {
#[test] test_no_verus_verify_attribute_on_impl_block_fails code!{
use vstd::prelude::*;
pub struct Foo;
impl Foo {
#[verus_verify]
#[verus_spec(ret =>
with
Tracked(c): Tracked<&mut ()>
requires
true,
ensures
ret == 1,
)]
fn test(a: u64, b: u64) -> u64 {
1
}
}
} => Err(_) => {}
}
test_verify_one_file! {
#[test] test_unverified_in_impl code!{
use vstd::prelude::*;
pub struct X;
#[verus_verify]
impl X {
fn unverified() {}
}
} => Ok(())
}
test_verify_one_file! {
#[test] test_item_const_dual code!{
use vstd::prelude::*;
#[verus_spec]
const CONST_ITEM: u64 = 42;
#[verus_spec]
fn test() {
let v = CONST_ITEM;
proof! {
assert(v == 42);
assert(CONST_ITEM == 42);
}
}
} => Ok(())
}
test_verify_one_file! {
#[test] test_item_const_error code!{
use vstd::prelude::*;
const CONST_ITEM: u64 = 42;
#[verus_spec]
fn test() {
let v = CONST_ITEM;
proof! {
assert(v == 42);
}
}
} => Err(e) => assert_any_vir_error_msg(e, "cannot use function `test_crate::CONST_ITEM` which is ignored")
}
test_verify_one_file! {
#[test] test_item_const_ensures code!{
use vstd::prelude::*;
#[verus_spec(ret=>
ensures ret == 42
)]
const fn const_item_fn() -> u64 {
42
}
#[verus_spec(
ensures CONST_ITEM == 42
)]
const CONST_ITEM: u64 = const_item_fn();
#[verus_spec]
fn test() {
let v = CONST_ITEM;
proof! {
assert(v == 42);
}
}
} => Ok(())
}
test_verify_one_file! {
#[test] test_item_const_ensures_is_exec_mode code!{
use vstd::prelude::*;
#[verus_spec(ret=>
ensures ret == 42
)]
const fn const_item_fn() -> u64 {
42
}
#[verus_spec(
ensures CONST_ITEM == 42
)]
const CONST_ITEM: u64 = const_item_fn();
#[verus_spec]
fn test() {
proof! {
assert(CONST_ITEM == 42);
}
}
} => Err(e) => assert_any_vir_error_msg(e, "cannot read const with mode exec")
}
test_verify_one_file! {
#[test] test_impl_item_const_dual code!{
use vstd::prelude::*;
struct X;
#[verus_verify]
impl X {
const A: usize = 1;
const B: usize = Self::A + 1;
const C: usize = Self::B + 1;
}
#[verus_spec(ensures true)]
fn test() {
let v = X::C;
proof! {
assert(v == 3);
assert(X::A == 1);
assert(X::B == 2);
assert(X::C == 3);
}
}
} => Ok(())
}
test_verify_one_file! {
#[test] test_impl_item_const_requires_erasure code!{
use vstd::prelude::*;
struct X;
#[verus_verify]
impl X {
const A: usize = 1;
}
// This requires to use const_proxy in const.
#[verus_verify]
enum Y {
A,
B = (1 << X::A) - 1,
}
} => Ok(())
}
test_verify_one_file! {
#[test] test_impl_item_const_use_unverified code!{
use vstd::prelude::*;
struct X;
const fn const_fn() -> u64 {
42
}
#[verus_verify]
impl X {
const CONST_ITEM: u64 = const_fn();
}
} => Err(e) => assert_any_vir_error_msg(e, "cannot use function `test_crate::const_fn` which is ignored")
}
test_verify_one_file! {
#[test] test_impl_item_const_external code!{
use vstd::prelude::*;
struct X;
const fn const_fn() -> u64 {
42
}
#[verus_verify]
impl X {
#[verus_verify(external)]
const CONST_ITEM: u64 = const_fn();
}
} => Ok(())
}
test_verify_one_file! {
#[test] test_impl_item_const_ensures code!{
use vstd::prelude::*;
struct X;
#[verus_spec(ret=>
ensures ret == 42
)]
const fn const_fn() -> u64 {
42
}
#[verus_verify]
impl X {
#[verus_spec(ensures Self::CONST_ITEM != 42)]
const CONST_ITEM: u64 = const_fn();
}
} => Err(e) => assert_any_vir_error_msg(e, "postcondition not satisfied")
}
test_verify_one_file! {
#[test] test_verus_spec_with_trailing_comma_simple code! {
use vstd::prelude::*;
#[verus_spec(ret =>
with
Tracked(y): Tracked<&mut u32>,
Ghost(w): Ghost<u32>,
requires
x < 100,
ensures
)]
fn foo(x: u32) -> u32 {
(x + 1)
}
#[verus_spec(ret =>
with
Tracked(y): Tracked<&mut u32>,
requires
x < 100,
)]
fn bar(x: u32) -> u32 {
(x + 1)
}
} => Ok(())
}
test_verify_one_file! {
#[test] test_verus_spec_with_trailing_comma_complex code!{
use vstd::prelude::*;
#[verus_spec(ret =>
with
Tracked(y): Tracked<&mut u32>,
Ghost(w): Ghost<u32>,
-> z: Ghost<u32>,
requires
x < 100,
ensures
ret == x + 1,
z@ == x,
)]
fn foo(x: u32) -> u32 {
proof_with!(|= Ghost(x));
(x + 1)
}
#[verus_spec(ret =>
with
Tracked(y): Tracked<&mut u32>,
Ghost(w): Ghost<u32>
-> z: Ghost<u32>,
requires
x < 100,
ensures
ret == x + 1,
z@ == x,
)]
fn bar(x: u32) -> u32 {
proof_with!(|= Ghost(x));
(x + 1)
}
#[verus_spec(ret =>
with
Tracked(y): Tracked<&mut u32>,
Ghost(w): Ghost<u32>,
-> z: Ghost<u32>
requires
x < 100,
ensures
ret == x + 1,
z@ == x,
)]
fn baz(x: u32) -> u32 {
proof_with!(|= Ghost(x));
(x + 1)
}
#[verus_spec(ret =>
with
Tracked(y): Tracked<&mut u32>,
Ghost(w): Ghost<u32>
-> z: Ghost<u32>
requires
x < 100,
ensures
ret == x + 1,
z@ == x,
)]
fn qux(x: u32) -> u32 {
proof_with!(|= Ghost(x));
(x + 1)
}
} => Ok(())
}
test_verify_one_file! {
#[test] test_erase_unverified_code code!{
use vstd::prelude::*;
#[verus_spec(
with Tracked(x): Tracked<()>,
ensures true,
)]
fn foo() {
proof!{
let abcd = Tracked(x);
let y = x;
}
#[cfg_attr(not(customized_cfg), verus_spec(
invariant x == (),
))]
for i in 0..10 {
}
}
} => Ok(())
}Automatically producing a spec function for executable code
When verifying code in Verus, it may be necessary to write spec functions that have the exact same implementation as their corresponding executable functions. This situation is common when the executable functions are small and purely computational.
#[verus_verify(dual_spec)] simplies the process of writing a spec function for an
existing executable function. When applied to an executable function, it
automatically produces a corresponding spec function by:
- Removing ghost variables and proof blocks from the executable function.
- Generating a spec function with identical logic. By default, the spec
function is given an internal name like _VERUS_SPEC_xxx. You can also specify
a custom name using
#[verus_verify(dual_spec($custom_name))]. - Applying the attribute
#[when_used_as_spec]to the executable function. Thus, the actual spec function name does generally matter since thewhen_used_as_specattribute allows you to use the executable function’s name directly as a spec function in proofs.
Here is an example:
#[verus_verify(dual_spec)]
#[verus_spec(
requires
x < 100,
y < 100,
returns f(x, y)
)]
fn f(x: u32, y: u32) -> u32 {
proof!{
assert(true);
}
{
proof!{assert(true);}
x + y
}
}
#[verus_verify(dual_spec)]
#[verus_spec(
requires
x < 100,
returns
f2(x),
)]
pub fn f2(x: u32) -> u32 {
f(x, 1)
}Limitations
#[verus_verify(dual_spec)] requires the use of #[verus_spec(...)]. It
currently does not support executable functions verified via the verus!
macro. This is because the verus_verify macro expects to parse an exec
function in native Rust syntax, instead of in verus! syntax. Thus,
#[verus_verify(dual_spec)] should be used with #[verus_spec(...)] outside
of the verus! macro.
dual_spec tries to generate a spec function from an exec function, but it may
not be able to generate a valid spec function if the exec function uses
features that are not supported by spec functions.
For example, mutable inputs are not supported:
fn f(x: &mut u32, y: u32) -> u32 {
*x = *x + y;
*x
}
If you use an unsupported feature, you should see the following error message:
The verifier does not yet support the following Rust feature
Related
The dual_spec attribute creates a spec function for executable code, which
might not cover your use case. For example, you may want to go from spec to
exec code, or use the when_used_as_spec attribute.
Spec expressions
Many built-in operators are in spec mode, i.e., they can be used in specification expressions. This section discusses those operators.
Rust subset
Much of the spec language looks like a subset of the Rust language, though there are some subtle differences.
Function calls
Only pure function calls are allowed (i.e., calls to other spec functions or
functions marked with the when_used_as_spec directive).
Let-assignment
Spec expressions support let-bindings, but not let mut-bindings.
if / if let / match statements
These work as normal.
&& and ||
These work as normal, though as all spec expressions are pure and effectless, there is no notion of “short-circuiting”.
Equality (==)
This is not the same thing as == in exec-mode; see more on ==.
Arithmetic
Arithmetic works a little differently in order to operate with Verus’s int
and nat types. See more on arithmetic.
References (&T)
Verus attempts to ignore Box and references as much as possible in spec mode.
However, you still needs to satisfy the Rust type-checker, so you may need to insert
references (&) or dereferences (*) to satisfy the checker. Verus will ignore these
operations however.
Box
Verus special-cases Box<T> along with box operations like Box::new(x) or *box
so they may be used in spec mode. Like with references, these operations are ignored,
however they are often useful. For example, to create a recursive type you need to satisfy
Rust’s sanity checks, which often involves using a Box.
Operator Precedence
| Operator | Associativity |
|---|---|
| Binds tighter | |
. -> | left |
is matches | left |
* / % | left |
+ - | left |
<< >> | left |
& | left |
^ | left |
| | left |
!== == != <= < >= > | requires parentheses |
&& | left |
|| | left |
==> | right |
<== | left |
<==> | requires parentheses |
.. | left |
= | right |
closures; forall, exists; choose | right |
&&& | left |
||| | left |
| Binds looser |
All operators that are from ordinary Rust have the same precedence-ordering as in ordinary Rust. See also the Rust operator precedence.
Arithmetic in spec code
Note: This reference page is about arithmetic in Verus specification code. This page is does not apply to arithmetic is executable Rust code.
For an introduction to Verus arithmetic, see Integers and arithmetic.
Type widening
In spec code, the results of arithmetic are automatically widened to avoid overflow or wrapping. The types of various operators, given as functions of the input types, are summarized in the below table. Note that in most cases, the types of the inputs are not required to be the same.
| operation | LHS type | RHS type | result type | notes |
|---|---|---|---|---|
<= < >= > | t1 | t2 | bool | |
== != | t1 | t2 | bool | |
+ | t1 | t2 | int | except for nat + nat |
+ | nat | nat | nat | |
- | t1 | t2 | int | |
* | t1 | t2 | int | except for nat * nat |
* | nat | nat | nat | |
/ | t | t | int | for i8…isize, int |
/ | t | t | t | for u8…usize, nat |
% | t | t | t | |
add(_, _) | t | t | t | |
sub(_, _) | t | t | t | |
mul(_, _) | t | t | t | |
& | ^ | t | t | t | |
<< >> | t1 | t2 | t1 |
Definitions: Quotient and remainder
In Verus specifications, / and % are defined by Euclidean division. Euclidean division may differ from the usual Rust / and % operators
when operands are negative.
For b != 0, the quotient a / b and remainder a % b are defined as the unique integers
q and r such that:
b * q + r == a0 <= r < |b|.
Note that:
- The remainder
a % bis always nonnegative - The quotient is “floor division” when b is positive
- The quotient is “ceiling division” when b is negative
Also note that a / b and a % b are unspecified when b == 0.
However, because all spec functions
are total, division-by-0 or mod-by-0 are not hard errors.
More advanced arithmetic
The Verus standard library includes the following additional arithmetic functions usable in spec expressions:
- Exponentiation (
vstd::arithmetic::power::pow) - Power of two (
vstd::arithmetic::power2::pow2) - Integer logarithm (
vstd::arithmetic::logarithm::log)
Bitwise ops
See bitwise operators.
Bit operators
Definitions
&, |, and ^
These have the usual meaning: bitwise-OR, bitwise-AND, and bitwise-XOR. Verus, like Rust, requires the input operands to be the same type, even in specification code. However, as binary operators defined over the integers, ℤ x ℤ → ℤ, these operations are independent of bitwidth. This is true even for negative operands, as a result of the way two’s complement sign-extension works.
>> and <<
Verus specifications, like Rust, does not require the left and right sides of a shift operator to be the same type. Shift is unspecified when the right-hand side is negative. Unlike in executable code, however, there is no upper bound on the right-hand side.
a << b and and a >> b both have the same type as a.
Right shifts can be defined over the integers ℤ x ℤ → ℤ independently of the input bitwidth.
For <<, however, the result does depend on the input type
because a left shift may involve truncation if some bits get shifted “off to the left”.
There is no widening to an int (unlike, say, Verus specification +).
Reasoning about bit operators
In Verus’s default prover mode, the definitions of these bitwise operators are not exported. To prove nontrivial facts about bitwise operators, use the bit-vector solver or the compute solver.
Coercion with as
In spec code, any “integer type” may be coerced to any other integer type via as.
For the sake of this page, “integer type” means any of the following:
i8,i16,i32,i64,i128,isizeu8,u16,u32,u64,u128,usizeintnatchar
Note that this is more permissive than as in Rust exec code. For example, Rust does
not permit using as to cast from a u16 to a char, but this is allowed in Verus
spec code.
Definition
Verus defines as-casting as follows:
- Casting to an
intis always defined and does not require truncation. - Casting to a
natis unspecified if the input value is negative. - Casting to a
charis unspecified if the input value is outside the allowedcharvalues. - Casting to any other finite-size integer type is defined as truncation — taking the lower N bits for the appropriate N, then interpreting the result as a signed or unsigned integer.
Reasoning about truncation
The definition of truncation is not exported in Verus’s default prover mode (i.e., it behaves as if it is unspecified). To reason about truncation, use the bit-vector solver or the compute solver.
Also note that the value of N for usize and isize may be configured with the global directive.
Spec equality (==)
The spec equality operator == is explained in Equality.
Extensional equality (=~= and =~~=)
The extensional equality operators =~= and =~~= are explained in
Extensional equality.
Prefix and/or (&&& and |||)
The prefix and/or operators (&&& and |||) are explained in Expressions and operators for specifications.
Chained operators
In spec code, equality and inequality operators can be chained. For example,
a <= b < c
is equivalent to
a <= b && b < c.
Chained inequalities support <, <=, >, >=, and ==, and support sequences of chained
operators of arbitrary length.
Implication (==>, <==, and <==>)
The operator P ==> Q, read P implies Q, is equivalent to !P || Q.
This can also be written backwards: Q <== P is equivalent to P ==> Q.
Finally, P <==> Q is equivalent to P == Q. It is sometimes useful for readability,
and because <==> has the same syntactic precedence as ==>
rather than the precedence of ==.
Spec quantifiers (forall, exists)
Quantifiers are explained in the Quantifiers part of the
tutorial. Specifically, forall is explained in forall and
triggers and exists is explained in exists and
choose.
Such that (choose)
The such-that operator (choose) is explained in exists and choose.
Trigger annotations
To every quantifier expression (forall, exists, choose) in the program, including “implicit”
quantifiers such as in broadcast lemmas.
There are many implications of triggers on proof automation that Verus developers should be aware of. See the relevant chapter of the guide, particulary the section on multiple triggers and matching loops.
This page explains the procedure Verus uses to determine these triggers from Verus source code.
Terminology: trigger groups and trigger expressions
Every quantifier has a number of quantifier variables. To control how the solver instantiates these variables, trigger groups are used.
- To every quantifier, Verus determines a collection of trigger groups.
- Every trigger group is a collection of trigger expressions.
By necessity, any trigger group is only well-formed if every quantifier variable is used by at least one trigger expression in the group.
Note that:
- The SMT solver will instantiate any quantifier whenever any trigger group fires.
- However, a trigger group will only fire if every expression in the group matches.
Therefore:
- Having more trigger groups makes the quantifier be instantiated more often.
- A trigger group with more trigger expressions will fire less often.
Selecting trigger groups
Verus determines the collection of trigger groups as follows:
- Verus finds all applicable
#[trigger]and#[trigger(n)]annotations in the body of the quantifier.- In the case of nested quantifiers, every
#[trigger]or#[trigger(n)]annotation is applicable to exactly one quantifier expression: the innermost quantifier which binds a variable used by the trigger expression.
- In the case of nested quantifiers, every
- All applicable expressions marked by
#[trigger]become a trigger group. - All applicable expressions marked by
#[trigger(n)]for the samenbecome a trigger group. - Every annotation
#![trigger EXPR1, …, EXPRk]at the root of the quantifier expression becomes a trigger group. - If, after all of the above, no trigger groups have been identified, Verus may use
heuristics to determine the trigger group(s) based on the body of the quantifier expression.
- If
#![all_triggers]is provided, Verus uses an “aggressive” strategy, choosing all trigger groups that can reasonably be inferred as applicable from the body. - If
#![auto]is provided, Verus uses a “conservative” strategy, choosing a single trigger group that is judged as optimal by various heuristics. - If neither
#![all_triggers]nor#![auto]are provided, Verus uses the same “conservative” strategy as it does for#![auto].
- If
- If, after all of the above, Verus is unable to find any trigger groups, it produces an error.
Trigger logging
By default, Verus often prints verbose information about selected triggers in cases where
Verus’s heuristics are “un-confident” in the selected trigger groups.
You can silence this information on a case-by-case basis using the #![auto] attribute.
When #![auto] is applied to a quantifier, this tells Verus
that you want the automatically selected triggers
even when Verus is un-confident, in which case this logging will be silenced.
The behavior can be configured through the command line:
| Option | Behavior |
|---|---|
--triggers-mode silent | Do not show automatically chosen triggers |
--triggers-mode selective | Default. Show automatically chosen triggers only when heuristics are un-confident, and when #![auto] has not been supplied |
--triggers | Show all automatically chosen triggers for verified modules |
--triggers-mode verbose | Show all automatically chosen triggers for verified modules and imported definitions from other module |
See more triggers logging options in verus --help
The view function @
The expression expr@ is a shorthand for expr.view(). The view() function is a Verus
convention for the abstraction of an exec-mode object, usually defined by the View trait.
However, the expansion of the @ syntax is purely syntactic, so it does not necessarily
correspond to the trait function.
Spec index operator []
In spec expressions, the index operator is treated differently than in exec expressions, where it corresponds to the usual Rust index operator.
Specifically, in a spec expression, the expression expr[i] is a shorthand for
expr.spec_index(i). This is a purely syntactic transformation, and there is no
particular trait.
For example:
decreases_to!
The expression decreases_to!(e1, e2, …, en => f1, f2, …, fn) is a bool indicating
if the left-hand sequence
e1, e2, …, en
lexicographically-decreases-to
the right-hand sequence
f1, f2, …, fn
The lexicographic-decreases-to
is used to check the decreases measure for spec functions.
See this tutorial chapter for an introductory discussion of lexicographic-decreases.
Definition
We say that
e1, e2, …, en
lexicographically-decreases-to
f1, f2, …, fn
if there exists a k where 1 <= k <= n such that:
ekdecreases-tofk.- For each
iwhere1 <= i < k,ei == fi.
The decreases-to relation is a partial order on all values; values of different types are comparable. The relation permits, but is not necessarily limited to:
- If
xandyare integers, wherex > y >= 0, thenxdecreases-toy. - If
ais a datatype (struct, tuple, or enum) andfis one of its “potentially recursive” fields, thenadecreases-toa.f.- For a datatype
X, a field is considered “potentially recursive” if it either mentionsXor a generic type parameter ofX.
- For a datatype
- If
fis aspec_fn, thenfdecreases-tof(i). - If
sis aSeq, thensdecreases-tos[i]. - If
sis aSeq, thensdecreases-tos.subrange(i, j)if the given range is strictly smaller than0 .. s.len().axiom_seq_len_decreasesprovides a more general axiom; it must be invoked explicitly.
- If
vis aVec, thenvdecreases-tov@.
These axioms are triggered when the relevant expression (e.g., x.f, x->f, s[i], v@) is used as part of a decreases-to expression.
Notes
-
Tuples are not compared lexicographically; tuples are datatypes, which are compared as explained above, e.g.,
adecreases_toa.0. Only the “top level” sequences in adecreases_to!expression are compared lexicographically. -
Sequences are not compared on
len()alone. However, you can always uses.len()as a decreases-measure instead ofs.
Examples
proof fn example_decreases_to(s: Seq<int>)
requires s.len() == 5
{
assert(decreases_to!(8int => 4int));
// fails: can't decrease to negative number
// assert(decreases_to!(8 => -2));
// Comma-separated elements are treated lexicographically:
assert(decreases_to!(12int, 8int, 1int => 12int, 4int, 50000int));
// Datatypes decrease-to their fields:
let x = Some(8int);
assert(decreases_to!(x => x->0));
let y = (true, false);
assert(decreases_to!(y => y.0));
// fails: tuples are not treated lexicographically
// assert(decreases_to!((20, 9) => (11, 15)));
// sequence decreases-to an element of the sequence
assert(decreases_to!(s => s[2]));
// sequence decreases-to a subrange of the sequence
assert(decreases_to!(s => s.subrange(1, 3)));
}assert … by
The assert ... by statement is used to encapsulate a proof. For a boolean spec expression, P, one writes:
assert(P) by {
// ... proof here
}
// ... remainderVerus will validate the proof and then attempt to use it to prove the P.
The contents of the proof, however, will not be included in the context used to
prove the remainder.
Only P will be introduced into the context for the remainder.
assert forall … by
The assert forall ... by statement is used to write a proof of a forall expression
while introducing the quantified variables into the context.
assert forall |idents| P by {
// ... proof here
}
// ... remainderMuch like an ordinary assert ... by statement, the proof
inside the body does not enter the context for the remainder of the proof.
Only the forall |idents| P expression enters the context.
Furthermore, within the proof body, the variables in the idents may be
Note that the parentheses must be left off, in contrast to other kinds of assert statements.
For convenience, you can use implies to introduce a hypothesis automatically into
the proof block:
assert forall |idents| H implies P by {
// ... proof here
}
// ... remainderThis will make H available in the proof block, so you only have to prove P.
In the end, the predicate forall |idents| H ==> P will be proved.
assert … by(bit_vector)
Invoke Verus’s bitvector solver to prove the given predicate. This is particularly useful for bitwise operators and integer arithmetic on finite-width integers. Internally, the solver uses a technique called bit-blasting, which represents each numeric variable by its binary representation as a bit vector, and every operation as a boolean circuit.
assert(P) by(bit_vector);
assert(P) by(bit_vector)
requires Q;
The prover does not have access to any prior context except that which is given in
the requires clause, if provided. If the requires clause is provided, then the
bit vector solver attempts to prove Q ==> P. Verus will also check (using its normal solver)
that Q holds from the prior proof context.
The expressions P and Q may only contain expressions that the bit solver understands.
This includes:
- Variables of type
boolor finite-width integer types (u64,i64,usize, etc.)- All free variables are treated symbolically. Even if a variable is defined via a
letstatement declared outside the bitvector assertion, this definition is not visible to the solver.
- All free variables are treated symbolically. Even if a variable is defined via a
- Integer and boolean literals
- Non-truncating arithmetic (
+,-,*,/, and%) - Truncating arithmetic (
add,sub,mulfunctions) - Bit operations (
&,|,^,!,<<,>>) - Equality and inequality (
==,!=,<,>,<=,>=) - Boolean operators (
&&,||,^) and conditional expressions - The
usize::BITSconstant
Internal operation
Verus’s bitvector solver encodes the expression by representing all integers using an SMT “bitvector” type. Most of the above constraints arise because of the fact that Verus has to choose a fixed bitwidth for any given expression.
Note that, although the bitvector solver cannot handle free variables of type
int or nat, it can handle other kinds of expressions that are typed int or nat.
For example, if x and y have type u64, then x + y has type int,
but the Verus bitvector solver knows that x + y is representable with 65 bits.
Handling usize and isize
If the expression uses any symbolic values whose width is architecture-dependent,
and the architecture bitwidth has not been specified via a global directive,
Verus will generate multiple queries, one for each possible bitwidth (32 bits or 64 bits).
assert … by(nonlinear_arith)
Invoke Z3’s nonlinear solver to prove the given predicate.
assert(P) by(bit_vector);
assert(P) by(bit_vector)
requires Q;
The solver uses Z3’s theory of nonlinear arithmetic. This can often solve problems
that involve multiplication or division of symbolic values. For example,
commutativity axioms like a * b == b * a are accessible in this mode.
The prover does not have access to any prior context except that which is given in
the requires clause, if provided. If the requires clause is provided, then the
bit vector solver attempts to prove Q ==> P. Verus will also check (using its normal solver)
that Q holds from the prior proof context.
assert … by(compute) / by(compute_only)
See this section of the tutorial for motivation and an example.
A statement of the form:
assert(P) by(compute_only);
Will evaluate the expression P as far a possible, and Verus accepts the result if it
evaluates to the boolean expression true. It unfolds function definitions and evaluates
arithmetic expressions. It is capable of some symbolic manipulation, but it does not handle
algebraic laws like a + b == b + a, and it works best when evaluating constant expressions.
Note that it will not substitute local variables, instead treating them as symbolic values.
This statement:
assert(P) by(compute);
Will first run the interpreter as above, but if it doesn’t succeed, it will then attempt
to finish the problem through the normal solver. So for example, if after expansion
P results in a trivial expression like a+b == b+a, then it should be solved
with by(compute).
Memoization
The #[verifier::memoize] attribute can be used to mark
certain functions for memoizing.
This will direct Verus’s internal interpreter to only evaluate the function once for any
given combination of arguments. This is useful for functions that would be impractical
to evaluate naively, as in this example:
#[verifier::memoize]
spec fn fibonacci(n: nat) -> nat
decreases n
{
if n == 0 {
0
} else if n == 1 {
1
} else {
fibonacci((n - 2) as nat) + fibonacci((n - 1) as nat)
}
}
proof fn test_fibonacci() {
assert(fibonacci(63) == 6557470319842) by(compute_only);
}reveal, reveal_with_fuel, hide
These attributes control whether and how Verus will unfold the definition of a spec function
while solving. For a spec function f:
reveal(f)directs Verus to unfold the definition offwhen it encounters a use off.hide(f)directs Verus to treatfas an uninterpreted function without reasoning about its definition.
Technically speaking, Verus handles “function unfolding” by
creating axioms of the form forall |x| f(x) == (definition of f(x)).
Thus, reveal(f) makes this axiom accessible to the solver,
while hide(f) makes this axiom inaccessible.
By default, functions are always revealed when they are in scope. This can be changed
by marking the function with the #[verifier::opaque] attribute.
The reveal_with_fuel(f, n) directive is used for recursive functions.
The integer n indicates how many times Verus should unfold a recursive function.
Limiting the fuel to a finite amount is necessary to avoid
trigger loops.
The default fuel (absent any reveal_with_fuel directive) is 1.
Exec fn signature
The general form of an exec function signature takes the form:
fn function_name generics?(args...) -> return_type_and_name?
where_clause?
requires_clause?
ensures_clause?
returns_clause?
invariants_clause?
unwind_clause?
Function specification
The elements of the function specification are given by the signature clauses.
The precondition.
The requires_clause is the precondition.
The postcondition.
The ensures_clause
and the
returns_clause
together form the postcondition.
The invariants.
The invariants_clause specifies what invariants can be opened by the function.
For exec functions, the default is open_invariants any.
See this page for more details.
Unwinding.
The unwind_clause specifies whether the function might exit “abnormally” by unwinding,
and under what conditions that can happen.
See this page for more details.
Function arguments
All arguments and return values need to have exec mode. To embed ghost/tracked variables into the signature, use the Tracked and Ghost types.
See here for more information.
Proof fn signature
The general form of a proof function signature takes the form:
proof fn function_name generics?(args...) -> return_type_and_name?
where_clause?
requires_clause?
ensures_clause?
returns_clause?
invariants_clause?
Function specification
The elements of the function specification are given by the signature clauses.
The precondition.
The requires_clause is the precondition.
The postcondition.
The ensures_clause
and the
returns_clause
together form the postcondition.
The invariants.
The invariants_clause specifies what invariants can be opened by the function.
For proof functions, the default is open_invariants none.
See this page for more details.
Function arguments
All arguments and return values need to have ghost or tracked mode.
Arguments are ghost by default, and they can be declared tracked with the tracked keyword.
See here for more information.
Spec fn signature
The general form of a spec function signature takes the form:
spec fn function_name generics?(args...) -> return_type?
where_clause?
recommends_clause?
decreases_clause?
The recommends clause
The recommends clauses is a “soft precondition”, which is sometimes checked for the sake
of diagnostics, but is not a hard requirement for the function to be well-defined.
See this guide page for motivation and overview.
The decreases clause
The decreases clause is used to ensure that recursive definitions are well-formed.
Note that if the decreases clauses has a when-subclause, it will restrict the function definition
to the domain.
See the reference page for decreases for more information,
or see the guide page on recursive functions for motivation and overview.
returns
The returns clause is syntactic sugar for an ensures clause of a certain form.
The returns clause can be provided instead of or in addition to an ensures clause.
The following:
fn example() -> return_type
returns $expr
{
...
}is equivalent to:
fn example() -> (return_name: return_type)
ensures return_name == $expr
{
...
}With the #![verifier::allow_in_spec] attribute
The #![verifier::allow_in_spec] attribute attribute can be applied to an executable function with a returns clause. This allows the function to be used in spec mode, where it is interpreted as equivalent to the specified return-value.
opens_invariants
The opens_invariants clause may be applied to any proof or exec function.
This indicates the set of names of tracked invariants that may be opened by the function.
At this time, it has three forms. See the documentation for open_local_invariant for more information about why Verus enforces these restrictions.
fn example()
opens_invariants any
{
// Any invariant may be opened here
}
or:
fn example()
opens_invariants none
{
// No invariant may be opened here
}
or:
fn example()
opens_invariants [ $EXPR1, $EXPR2, ... ]
{
// Only invariants with names in [ $EXPR1, $EXPR2, ... ] may be opened.
}
Defaults
For exec functions, the default is opens_invariants any.
For proof functions, the default is opens_invariants none.
Unwinding signature
For any exec-mode function, it is possible to specify whether that function may unwind. The allowed forms of the signature are:
- No signature (default) - This means the function may unwind.
no_unwind- This means the function may not unwind.no_unwind when {boolean expression in the input arguments}- If the given condition holds, then the call is guaranteed to not unwind.no_unwind when trueis equivalent tono_unwindno_unwind when falseis equivalent to the default behavior
By default, a function is allowed to unwind. (Note, though, that Verus does rule out common sources of unwinding, such as integer overflow, even when the function signature technically allows unwinding.)
Example
Suppose you want to write a function which takes an index, and that you want to specify:
- The function will execute normally if the index is in-bounds
- The function will unwind otherwise
You might write it like this:
fn get(&self, i: usize) -> (res: T)
ensures i < self.len() && res == self[i]
no_unwind when i < self.len()This effectively says:
- If
i < self.len(), then the function will not unwind. - If the function returns normally, then
i < self.len()(equivalently, ifi >= self.len(), then the function must unwind).
Restrictions with invariants
You cannot unwind when an invariant is open. This restriction is necessary because an unwinding operation does not necessarily abort a program. Rust allows a program to “catch” an unwind, for example, or there might be other threads to continue execution. As a result, Verus cannot permit the program to exit an invariant-block early without restoring the invariant, not even for unwinding.
This is restriction is what enables Verus to rule out exception safety violations.
Drops
If you implement Drop for a type, you are required to give it a signature of no_unwind.
recommends
See this guide page for motivation and overview.
Signature inheritance
Usually, the developer does not write a signature for methods in a trait implementation, as the signatures are inherited from the trait declaration. However, the signature can be modified in limited ways. To ensure soundness of the trait system, Verus has to make sure that the signature on any function must be at least as strong as the corresponding signature on the trait declaration.
- All
requiresclauses in a trait declaration are inherited in the trait implementation. The user cannot add additionalrequiresclauses in a trait implementation. - All
ensuresclauses in a trait declaration are inherited in the trait implementation. Furthermore, the user can add additionalensuresclauses in the trait implementation. - The
opens_invariantssignature is inherited in the trait implementation and cannot be modified. - The unwinding signature is inherited in the trait implementation and cannot be modified.
When a trait function is called, Verus will attempt to statically resolve the function to a particular trait implementation. If this is possible, it uses the possibly-stronger specification from the trait implementation; in all other cases, it uses the generic specification from the trait declaration.
Specifications on FnOnce
For any function object, i.e., a value of any type that implements FnOnce
(for example, a named function, or a closure) the signature can be reasoned about generically
via the Verus built-in functions call_requires and call_ensures.
call_requires(f, args)is a predicate indicating iffis safe to call with the givenargs. For any non-static call, Verus requires the developer to prove thatcall_requires(f, args)is satisfied at the call-site.call_ensures(f, args, output)is a predicate indicating if it is possible forfto return the givenoutputwhen called withargs. For any non-static call, Verus will assume thatcall_ensures(f, args, output)holds after the call-site.- At this time, the
opens_invariantsaspect of the signature is not treated generically. Verus conservatively treats any non-static call as if it might open any invariant.
The args is always given as a tuple (possibly a 0-tuple or 1-tuple).
See the tutorial chapter for examples and more tips.
For any function with a Verus signature (whether a named function or a closure), Verus generates axioms resembling the following:
(user-declared requires clause) ==> call_requires(f, args)
call_ensures(f, args, output) ==> (user-declared ensures clauses)
Using implication (==>) rather than a strict equivalence (<==>) in part to allow
flexible signatures in traits.
However, our axioms use this form for all functions, not just trait functions.
This form reflects the proper way to write specifications for higher-order functions.
External trait specifications
When writing verified code that interacts with external Rust libraries, you may need to add specifications to traits defined in those libraries. Verus provides two attributes for this purpose:
#[verifier::external_trait_specification]— adds requires/ensures to trait methods#[verifier::external_trait_extension]— additionally defines spec helper functions on the trait
Soundness warning
Be cautious when adding specifications to external traits. All implementations
of the trait — including those in unverified code, even code that hasn’t been written yet — are
assumed to uphold the specification. For example, if you verify a crate with
pub fn test<A: Formatter>(...), Verus assumes that whatever type instantiates A will
satisfy the Formatter specification, even if that type comes from an unverified crate.
This is a contract on both current and future unverified code.
See below for a useful pattern (employed by vstd) for mitigating this soundness risk.
Basic external trait specification
Suppose we have an external trait:
#[verifier::external]
trait Encoder {
fn encode_value(&self, x: u64) -> u64;
}We can add specifications to it with #[verifier::external_trait_specification]:
#[verifier::external_trait_specification]
trait ExEncoder {
// This associated type names the trait being specified:
type ExternalTraitSpecificationFor: Encoder;
fn encode_value(&self, x: u64) -> (result: u64)
ensures
result >= x;
}Key points about this syntax:
- The specification trait (here
ExEncoder) must contain a specially named associated typeExternalTraitSpecificationForwhose bound names the external trait being specified. - The trait name
ExEncoderis arbitrary and is not used elsewhere. - Method signatures must match the external trait, but you can add
requiresandensuresclauses, and you can give a name to the return value (e.g.,(result: u64)) for use inensures. - The specification trait is not required to include all members of the external trait. Members that are not included are not accessible to verified code.
With the specification in place, verified code can use the trait:
fn use_encoder<E: Encoder>(f: &E, val: u64) -> (result: u64)
ensures
result >= val,
{
f.encode_value(val)
}External trait extension (spec helper functions)
Sometimes, a trait specification needs additional spec-mode functions that don’t
exist in the original trait. For example, you may want a spec function that describes the
abstract behavior of a method. The #[verifier::external_trait_extension] attribute supports this.
The attribute takes the form:
#[verifier::external_trait_extension(SpecTrait via SpecImplTrait)]
- SpecTrait is the name of a spec-mode trait that becomes available in verification. It is automatically implemented for any type implementing the external trait.
- SpecImplTrait is the name of a trait that concrete types implement to define the spec helper functions.
Here is an example, using a fictitious external trait named Summarizer:
#[verifier::external_trait_specification]
#[verifier::external_trait_extension(SummarizerSpec via SummarizerSpecImpl)]
trait ExSummarizer {
type ExternalTraitSpecificationFor: Summarizer;
// A spec helper function (not part of the original trait):
spec fn spec_summary(&self) -> u64;
fn summary(&self) -> (result: u64)
ensures
result == self.spec_summary();
}Concrete types implement SpecImplTrait (here SummarizerSpecImpl) to define the spec helpers,
and can then use the specifications in verified code:
struct MyCustomStruct { value: u64 }
// Implement the concrete external Summarizer trait
impl Summarizer for MyCustomStruct {
fn summary(&self) -> u64 {
// Prove that our overly complicated implementation satisfies the spec_summary
let v = self.value;
assert(v & 0xffff_ffff_ffff_ffff == v) by (bit_vector);
v & 0xffff_ffff_ffff_ffff
}
}
// Implement the additional spec functions
impl SummarizerSpecImpl for MyCustomStruct {
spec fn spec_summary(&self) -> u64 {
self.value
}
}
fn test_hasher(h: &MyCustomStruct) {
let v = h.summary();
assert(v == h.value);
}The obeys_* pattern in vstd
vstd uses external_trait_extension extensively for standard library traits like PartialEq,
Ord, Add, From, etc. These specifications follow a common pattern using an obeys_*
spec function that indicates whether a given type implementation actually follows the
specification.
For example, vstd’s specification for PartialEq looks roughly like this:
#[verifier::external_trait_specification]
#[verifier::external_trait_extension(PartialEqSpec via PartialEqSpecImpl)]
pub trait ExPartialEq<Rhs = Self> {
type ExternalTraitSpecificationFor: PartialEq<Rhs>;
spec fn obeys_eq_spec() -> bool;
spec fn eq_spec(&self, other: &Rhs) -> bool;
fn eq(&self, other: &Rhs) -> (r: bool)
ensures
Self::obeys_eq_spec() ==> r == self.eq_spec(other);
}The ensures clause says: if the type obeys the Verus spec for Eq (obeys_eq_spec() is true), then
the result matches eq_spec. For integer types and bool, vstd defines obeys_eq_spec()
to be true, and proves that these types satisfy the eq_spec. For other types, Verus
doesn’t know whether obeys_eq_spec() is true or false, so it won’t assume that the postcondition
holds. This pattern lets vstd provide useful specifications for well-behaved types without making
unsound assumptions about all types. If you want to use a trait like Eq for an external type,
you can use an assume_specification
to say that obeys_eq_spec() is true.
Rules and restrictions
- The
ExternalTraitSpecificationForassociated type is required and must name the external trait. - The specification trait should not have a body for any method.
- Generic parameters and associated types must match the external trait exactly.
- When using
external_trait_extension, the two names (SpecTraitandSpecImplTrait) become real trait names;SpecTraitcan be used in bounds andSpecImplTraitcan be used inimplblocks.
decreases … when … via …
The decreases clause is necessary for ensuring termination of recursive and mutually-recursive
functions. See this tutorial page for an introduction.
Overview
A collection of functions is mutually recursive if their call graph is strongly connected (i.e., every function in the collection depends, directly or indirectly, on every function in the collection). (A single function that calls itself forms a mutually recursive collection of size 1.) A function is recursive if it is in some mutually recursive collection.
A recursive spec function is required to supply a decreases clause, which takes
the form:
decreases EXPR_1, ...
[ when BOOL_EXPR ]?
[ via FUNCTION_NAME ]?The sequence of expressions in the decreases clause is the decreases-measure.
The expressions in the decreases-measure and the expression in the when-clause
may reference the function’s arguments.
Verus requires that, for any two mutually recursive functions, the number of elements in their decreases-measure must be the same.
The decreases-measure
Verus checks that, when a recursive function calls itself or any other function in its mutually recursive collection, the decreases-measure of the caller decreases-to the decreases-measure of the callee. See the formal definition of decreases-to.
The when clause
If the when clause is supplied, then the given condition may be assumed when
proving the decreases properties.
However, the function definition will only be concretely specified when the when clause is true.
In other words, something like this:
fn f(...) -> _
decreases ...
when condition
{
body
}Will be equivalent to this:
fn f(args...) -> _
{
if condition {
body
} else {
some_unknown_function(args...)
}
}Helping Verus prove termination
Sometimes, it may be true that the decreases-measure decreases, but Verus cannot prove it automatically. When this happens, the user can either supply a proof inside the body of the recursive function, or use a separate lemma to prove the decreases property. In the vast majority of cases, writing a proof inside the function body is simpler and easier to read. The main reason to use a separate lemma is if you want to keep your trusted specifications as minimal as possible.
Example.
On its own, Verus cannot see that n decreases at each recursive call.
We’ll use this example to illustrate the two methods of helping Verus prove termination.
spec fn floor_log2(n: u64) -> int
decreases n
{
if n <= 1 {
0
} else {
floor_log2(n >> 1) + 1
}
}In order to check that the recursion in floor_log2 terminates, Verus generates a proof obligation
that n > 1 ==> decreases_to!(n => n >> 1). (The n > 1 hypothesis stems from the fact that
the recursive call is in the else-block.) Thus we need to show:
n > 1 ==> (n >> 1) < n
Verus cannot prove this automatically.
Writing an proof of termination inside your recursive function
For the purposes of termination checking, you can include a proof {} block
in the body of your spec function. The proof needs to demonstrate that your
decreases measure really does decrease at each recursive call site.
Note that at present, this proof block can only assist with termination. You cannot use it, for example, to prove additional properties about your function for use elsewhere.
Example Here we supply the fact Verus was missing using Verus’s specialized bit-vector reasoning mode.
spec fn floor_log2(n: u64) -> int
decreases n
{
if n <= 1 {
0
} else {
proof {
assert(n > 1 ==> (n >> 1) < n) by(bit_vector);
}
floor_log2(n >> 1) + 1
}
}Writing a separate proof of termination with the via clause
To avoid cluttering your recursive spec function with proof material,
you can add a via PROOF_FUNCTION_NAME clause to the spec function.
FUNCTION_NAME must be the name of a proof function defined in the same module
that takes the same arguments as the recursive function.
This proof function must also be annotated with the #[via_fn] attribute.
The proof function’s job is to prove the relevant decreases property for each call site. In other words, it needs to show that the decreases measure actually decreases at each recursive call in the spec function’s body.
Example.
In the following definition, we use a via clause to prove that the decreases-measure
decreases.
spec fn floor_log2_via(n: u64) -> int
decreases n
via floor_log2_decreases_proof
{
if n <= 1 {
0
} else {
floor_log2_via(n >> 1) + 1
}
}
#[via_fn]
proof fn floor_log2_decreases_proof(n: u64) {
assert(n > 1 ==> (n >> 1) < n) by(bit_vector);
}The proof function floor_log2_decreases_proof is defined as a via_fn and is referenced from the via clause. The body of the proof function contains a proof that n > 1 ==> (n >> 1) < n (the same proof we used inline above).
Type invariants
Structs and enums may be augmented with a type invariant, a boolean predicate indicating well-formedness of a value. The type invariant applies to any exec object or tracked-mode ghost object and does not apply to spec objects.
Type invariants are primarily intended for encapsulating and hiding invariants.
Declaring a type invariant
A type invariant may be declared with the #[verifier::type_invariant] attribute.
It can be declared either as a top-level item or in an impl block.
#[verifier::type_invariant]
spec fn type_inv(x: X) -> bool { ... }impl X {
#[verifier::type_invariant]
spec fn type_inv(self) -> bool { ... }
}It can be inside an impl block and take self, of it can be declared as a top-level item.
It can have any name.
The invariant predicate must:
- Be a spec function of type
(X) -> boolor(&X) -> bool, whereXis the type the invariant is applied to. - Be applied to a datatype (
structorenum) that:- Is declared in the same crate
- Has no fields public outside of the crate
There is no restriction that the type invariant function have the same visibility as the type it is declared for, only that it is visible whenever the type invariant needs to be asserted or assumed (as described below). Since type invariants are intended for encapsulation, it is recommended that they be as private as possible.
Enforcing that the type invariant holds
For any type X with a type invariant,
Verus enforces that the predicate always hold for any exec object or tracked-mode ghost object
of type X. Therefore, Verus add a proof obligation that the predicate holds:
- For any constructor expression of
X - After any assignment to a field of
X - After any function call that takes a mutable borrow to
X
Currently, there is no support for “temporarily breaking” a type invariant, though this capability may be added in the future. This can often be worked around by taking mutable borrows to the fields.
Applying the type invariant
Though the type invariant is enforced automatically, it is not provided to the user automatically.
For any object x: X with a type invariant, you can call the builtin pseudo-lemma use_type_invariant to learn that the type invariant holds on x.
use_type_invariant(&x);
The value x must be a tracked or exec variable.
This statement is a proof feature, and if it appears in an exec function, it must be in
a proof block.
Example
struct X {
i: u8,
j: u8,
}
impl X {
#[verifier::type_invariant]
spec fn type_inv(self) -> bool {
self.i <= self.j
}
}
fn example(x: X) {
proof {
use_type_invariant(&x);
}
assert(x.i <= x.j); // succeeds
}
fn example_caller() {
let x = X { i: 20, j: 30 }; // succeeds
example(x);
}
fn example_caller2() {
let x = X { i: 30, j: 20 }; // fails
example(x);
}Attributes
accept_recursive_typesall_triggersallow_complex_invariantsallow_in_specatomicautoexternalexternal_bodyexternal_fn_specificationexternal_type_specificationext_equalinlineloop_isolationmemoizeopaquereject_recursive_typesreject_recursive_types_in_ground_variantsrlimittriggertruncatetype_invariantwhen_used_as_specexec_allows_no_decreases_clauseassume_termination
#![all_triggers]
Applied to a quantifier, and instructs Verus to aggressively select trigger groups for the quantifier. See the trigger specification procedure for more information.
Unlike most Verus attributes, this does not require the verifier:: prefix.
#[verifier::allow_complex_invariants]
By default, invariant_except_break and ensures are not supported with
#[verifier::loop_isolation(false)] because they
aren’t needed. When loop isolation is disabled, the weakest precondition
calculation automatically tracks all paths through breaks into the code after
the loop, making these complex invariant types unnecessary.
However, in some cases (such as experimenting with toggling the loop isolation setting,
or for our de-sugaring of for-loops), it can be useful to use these invariant types even with loop isolation disabled.
The allow_complex_invariants attribute enables this by transforming the invariants:
invariant_except_breakclauses are converted to regularinvariantclausesensuresclauses are ignored (since they are redundant with the weakest precondition calculation)
This attribute only applies when loop_isolation is false. Using it with loop_isolation(true)
(or the default) will produce an error.
#![verifier::allow_in_spec]
Can be applied to an executable function with a returns clause.
This allows the function to be used in spec mode, where it is interpreted as equivalent
to the specified return-value.
#[verifier::atomic]
The attribute #[verifier::atomic] can be applied to any exec-mode function to indicate
that it is “atomic” for the purposes of the atomicity check by
open_atomic_invariant!.
Verus checks that the body is indeed atomic, unless the function is also marked
external_body, in which case this feature is assumed together with the rest of the function
signature.
This attribute is used by vstd’s trusted atomic types.
#![auto]
Applied to a quantifier, and indicates intent for Verus to use heuristics to automatically infer Technically has no effect on verification, but may impact verbose trigger logging. See the trigger specification procedure for more information.
Unlike most Verus attributes, this does not require the verifier:: prefix.
#[verifier::external]
Tells Verus to ignore the given item. Verus will error if any verified code attempts to reference the given item.
This can have nontrivial implications for the TCB of a verified crate; see here.
#[verifier::external_body]
Tells Verus to only consider the function definition but not the function body, trusting that it correctly satisfies its specification.
This can have nontrivial implications for the TCB of a verified crate; see here.
#[verifier::ext_equal]
Used to mark datatypes that need extensionality on Seq, Set, Map,
Multiset, spec_fn fields or fields of other #[verifier::ext_equal]
datatypes.
See the discussion of equality via extensionality for more information.
#[verifier::inline]
The attribute #[verifier::inline] can be applied to any spec-mode function to indicate
that that Verus should automatically expand its definition in the STM-LIB encoding.
This has no effect on the semantics of the function but may impact triggering.
#[verifier::loop_isolation]
The attributes #[verifier::loop_isolation(false)] and #[verifier::loop_isolation(true)]
can be applied to modules, functions, or individual loops. For any loop, the most specific
applicable attribute will take precedence.
This attribute impacts the deductions that Verus can make automatically inside the loop
body (absent any loop invariants).
- When set to
true: Verus does not automatically infer anything inside the loop body, not even function preconditions. - When set the
false: Verus automatically makes some facts from outside the loop body available in the loop body. In particular, any assertion outside the loop body that depends only on variables not mutated by the loop body will also be available inside the loop.
#[verifier::memoize]
The attribute #[verifier::memoize] can be applied to any spec-mode function to indicate
that the by(compute) and by(compute_only) prover-modes
should “memoize” the results of this function.
#[verifier::opaque]
Directs the solver to not automatically reveal the definition of this function.
The definition can then be revealed locally via the reveal and reveal_with_fuel directives.
#[verifier::rlimit(n)] and #[verifier::rlimit(infinity)]
The rlimit option can be applied to any function to configure the computation limit
applied to the solver for that function.
The default rlimit is 10. The rlimit is roughly proportional to the amount of time taken
by the solver before it gives up. The default, 10, is meant to be around 2 seconds.
The rlmit may be set to infinity to remove the limit.
The rlimit can also be configured with the --rlimit command line option.
#[trigger]
Used to manually specify trigger groups for a quantifier. See the trigger specification procedure for more information.
Unlike most Verus attributes, this does not require the verifier:: prefix.
#[verifier::truncate]
The #[verifier::truncate] attribute can be added to expressions to silence
recommends-checking regarding out-of-range as-casts.
When casting from one integer
type to another, Verus usually inserts recommends-checks that the source
value fits into the target type. For example, if x is a u32 and we cast it
via x as u8, Verus will add a recommends-check that 0 <= x < 256.
However, sometimes truncation is the desired behavior, so
#[verifier::truncate] can be used to signal this intent, suppressing
the recommends-check.
Note that the attribute is optional, even when truncation behavior is intended. The only effect of the attribute is to silence the recommends-check, which is already elided if the enclosing function body has no legitimate verification errors.
Aside. When truncation is intended, the bit-vector solver mode is often useful for writing proofs about truncation.
#[verifier::type_invariant]
Declares that a spec function is a type invariant for some datatype. See type invariants.
#[verifier::when_used_as_spec]
It can be convenient to use the name of an exec function in a specification
context. For example, if a function takes v: Vec<u64> as an argument, it’s
convenient to use v.len() in the pre-/post-conditions, even though v.len()
is an exec function. To add such a shortcut to your code, add a
#[verifier::when_used_as_spec(your_spec_fn_name)] attribute to your
executable function. For this to work, the supplied spec function (e.g., named
your_spec_fn_name in the example above) must take the same number and type of
arguments and return the same return type as the exec function.
#[verifier::exec_allows_no_decreases_clause]
Disables the requirement that exec functions with recursion or loops have a decreases clause. Can be applied to a function, module, or crate, affects all the contents.
#[verifier::assume_termination]
Assumes that an exec function is guaranteed to terminate, even if it does not have a decreases clause.
This is currently unneeded, as exec termination checking does not check that callees also terminate.
assume_specification
The assume_specification directive tells Verus to use the given specification for the given function.
Verus assumes that this specification holds without proof.
It can be used with any exec-mode function that Verus would otherwise be unaware of; for example,
any function marked external or which is imported from an external crate.
It is similar to having a function which is external_body; the difference is that when assume_specification is used, the specification is separate from the function declaration
and body.
The assume_specification declaration does NOT have to be in the same module or crate
as its corresponding function. However:
- The function must be visible to its
assume_specificationdeclaration - The
assume_specificationdeclaration must be visible wherever the function is visible.
The general form of this directive is:
assume_specification generics? [ function_path ] (args...) -> return_type_and_name?
where_clause?
requires_clause?
ensures_clause?
returns_clause?
invariants_clause?
unwind_clause?
;
It is intended to look like an ordinary Rust function signature with a Verus specification, except instead of having a name, it refers to a different function by path.
For associated functions and methods, the function_path should have the form Type::method_name,
using “turbofish syntax” for the type (e.g., Vec::<T>).
For trait methods, the function_path should use the “qualified self” form, <Type as Trait>::method_name.
The signature must be the same as the function in question, including arguments, return type, generics, and trait bounds.
All arguments should be named and should not use self.
Examples
To apply to an ordinary function:
pub assume_specification<T> [core::mem::swap::<T>] (a: &mut T, b: &mut T)
ensures
*a == *old(b),
*b == *old(a),
opens_invariants none
no_unwind;To apply to an associated function of Vec:
pub assume_specification<T>[Vec::<T>::new]() -> (v: Vec<T>)
ensures
v@ == Seq::<T>::empty();To apply to an method of Vec:
pub assume_specification<T, A: Allocator>[Vec::<T, A>::clear](vec: &mut Vec<T, A>)
ensures
vec@ == Seq::<T>::empty();To apply to clone for a specific type:
pub assume_specification [<bool as Clone>::clone](b: &bool) -> (res: bool)
ensures res == b;The “global” directive
In most cases, Verus has no access to layout information, such as the size
(std::mem::size_of::<T>())
or alignment (std::mem::align_of::<T>())
of a struct.
Such information is often unstable (i.e., it may vary between versions of Rust)
or may be platform-dependent (such as the size of usize).
Though vstd does provide some axioms for stable, platform-independent layout information,
(e.g., for primitives and pointer types), in most cases you will need to deal with types that have unstable layouts.
This information can be provided to Verus as needed using the global directive.
For a type T, and integer literals n or m, the global directive is a Verus item
that takes the form:
global layout T is size == n, align == m;Either size or align may be omitted. The global directive both:
- Exports the axioms
size_of::<T>() == nandalign_of::<T> == mfor use in Verus proofs - Creates a “static” check ensuring the given values are actually correct when compiled.
Note that the second check only happens when codegen is run; an “ordinary” verification pass will not perform this check. This ensures that the check is always performed on the correct platform, but it may cause surprises if you spend time on verification without running codegen.
In order to keep the layout stable, it is recommended using Rust attributes
like #[repr(C)].
Keep in mind that the Verus verifier gets no information from these attributes.
Layout information can only be provided to Verus via the global directive.
With usize and isize
For the integer types usize and isize, the global directive has additional behavior.
Specifically, it influences the integer range used in encoding usize and isize types.
For an integer literal n, the directive,
global layout usize is size == n;
Tells Verus that:
usize::BITS == 8 * nisize::BITS == 8 * n- The integer range for
usize(usize::MIN ..= usize::MAX) is0 ..= 28*n - 1 - The integer range for
isize(isize::MIN ..= isize::MAX) is-28*n-1 ..= 28*n-1 - 1
By default (i.e., in the absence of a global directive regarding usize or isize),
Verus assumes that the size is either 4 or 8, i.e., that the integer range is
either 32 bits or 64 bits.
Example
global layout usize is size == 4;
fn test(x: usize) {
// This passes because Verus assumes x is a 32-bit integer:
assert(x <= 0xffffffff);
assert(usize::BITS == 32);
}
Static items
Verus supports static items, similar to const items. Unlike const items, though,
static items are only usable in exec mode. Note that this requires them to be
explicitly marked as exec:
exec static x: u64 = 0;
The reason for this is consistency with const; for const items, the default mode
for an unmarked const item is the dual spec-exec mode.
However, this mode is not supported for static items; therefore, static items
need to be explicitly marked exec.
Note there are some limitations to the current support for static items.
Currently, a static item cannot be referenced from a spec expression. This means, for example,
that you can’t prove that two uses of the same static item give the same value
if those uses are in different functions. We expect this limitation will be lifted
in the future.
The char primitive
Citing the Rust documentation on char:
A char is a ‘Unicode scalar value’, which is any ‘Unicode code point’ other than a surrogate code point. This has a fixed numerical definition: code points are in the range 0 to 0x10FFFF, inclusive. Surrogate code points, used by UTF-16, are in the range 0xD800 to 0xDFFF.
Verus treats char similarly to bounded integer primitives like u64 or u32: We represent
char as an integer. A char always carries an invariant that it is in the prescribed set
of allowed values:
[0, 0xD7ff] ∪ [0xE000, 0x10FFFF]
In spec code, chars can be cast to and from other integer types using as.
This is more
permissive than exec code, which disallows many of these coercions.
As with other coercions, the result may be undefined if the integer being coerced does not
fit in the target range.
Unions
Verus supports Rust unions.
Internally, Verus represents unions a lot like enums. However, Rust syntax for accessing
unions is different than enums. In Rust, a field of a union is accessed with field access:
u.x. Verus allows this operation in exec-mode, and Verus always checks it is well-formed,
i.e., it checks that u is the correct “variant”.
In spec-mode, you can use the built-in spec operators is_variant and get_union_field
to reason about a union. Both operators refer to the field name via string literals.
is_variant(u, "field_name")returns true ifuis in the"field_name"variant.get_union_field::<U, T>(u, "field_name")returns a value of typeT, whereTis the type of"field_name". (Verus will error ifTdoes not match between the union and the generic parameterTof the operator.)
Example
union U {
x: u8,
y: bool,
}
fn union_example() {
let u = U { x: 3 };
assert(is_variant(u, "x"));
assert(get_union_field::<U, u8>(u, "x") == 3);
unsafe {
let j = u.x; // this operation is well-formed
assert(j == 3);
let j = u.y; // Verus rejects this operation
}
} Note on unsafe
The unsafe keyword is needed to satisfy Rust, because Rust treats union field access
as an unsafe operation. However, the operation is safe in Verus because Verus is able to
check its precondition. See more on how Verus handles memory safety.
Pointers and cells
See the vstd documentation for more information on handling these features.
- For cells, see
PCell - For pointers to fixed-sized heap allocations, see
PPtr. - For general support for
*mut Tand*const T, seevstd::raw_ptr
Record flag
Sometimes, you might wish to record an execution trace of Verus to share, along with all the necessary dependencies to reproduce an execution. This might be useful for either packaging up your verified project, or to report a Verus bug to the issue tracker.
The --record flag will do precisely this. In particular, to record an execution of Verus (say, verus foo --bar --baz), simply add the --record flag (for example, verus foo --bar --baz --record). This will re-run Verus, and package all the relevant source files, along with the execution output and version information into a zip file (yyyy-mm-dd-hh-mm-ss.zip) in your current directory.